[JAVA] DP(Dynamic Programming)

beegle·2025년 3월 23일

자료구조&알고리즘

목록 보기

5/6

동적 계획법(Dynamic Programming)

동적계획법(Dynamic Programming, DP)의 정의는 복잡한 문제를 간단한 여러 개의 문제로 나누어 푸는 방법을 말한다. 즉, 문제에서 요구하는 정답을 구하기 위해 문제를 여러 개의 하위 문제로 나누어서 푸는 방법을 말한다.

각 하위 문제의 해를 구한 다음 저장해놓고 다음에 같은 하위 문제가 나왔을 때 바로 해를 구할 수 있다. 이런 식으로 계산 횟수를 줄일 수 있다.

그래서 DP는 부분 문제 반복(Overlapping Subproblem)과 최적 부분 구조(Optimal Substructure)를 가지고 있는 경우에 적용할 수 있다.

부분 문제 반복

부분 문제 반복(Overlapping Subproblem) 은 어떤 문제가 여러 개의 부분 문제(subproblem)으로 쪼개질 수 있을 때 사용하는 용어이다.

이 때 '부분문제' 란, 항상 새로운 부분 문제를 생성해내기 보다는 계속해서 같은 부분 문제가 여러번 재사용되거나 재귀 알고리즘을 통해 해결되는 문제를 가리킨다.

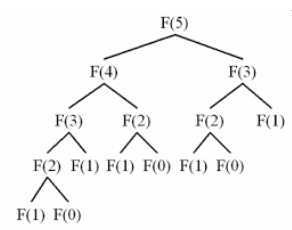
대표적인 예로 피보나치 수를 들 수 있다. 피보나치 수열은 이전 두 수를 더한 수가 다음 수가 되는 수열이다.

N번째 피보나치 수 = N-1번째 피보나치 수 + N-2번째 피보나치 수

N-1번째 피보나치 수 = N-2번째 피보나치 수 + N-3번째 피보나치 수

N-2번째 피보나치 수 = N-3번째 피보나치 수 + N-4번째 피보나치 수

수식으로 표현하면, 아래와 같다.

f(n)=f(n−1)+f(n−2)

f(n−1)=f(n−2)+f(n−3)

f(n−2)=f(n−3)+f(n−4)

f(n)를 구하기 위해서는 f(n-1) 과 f(n-2) 가 필요합니다. 여기서 f(n-2) 는 이미 f(n-1) 을 구하는 과정에서 값을 구한 문제다.

또한 f(n)의 f(n-1) 구하는 과정은 f(n) 을 구하는 방식과 같아 재귀 알고리즘으로 해결된다는 것을 확인할 수 있다.

이와 같이 사용되었지만 다시 재사용되거나 재귀를 통해서 해결되는 문제들이 반복되는 것을 부분 문제 반복이라 한다.

최적 부분 구조

최적 부분 구조(Optimal Substructure)는 어떤 문제의 최적의 해결책이 그 부분 문제의 최적의 해결책으로 설계될 수 있는 경우를 말한다.

즉, 최적 부분 구조일 때 문제의 정답을 작은 문제의 정답에서부터 구할 수 있음을 말한다.

예를 들어, 최단 경로를 찾는 문제를 들 수 있다.

문제 : 서울에서 대전을 거쳐 부산까지 가는 가장 빠른 경로를 찾아라.
서울에서 대전까지 가는 가장 빠른 경로를 찾아라. 서울 -> 광명 -> 대전
대전에서 부산까지 가는 가장 빠른 경로를 찾아라. 대전 -> 대구 -> 부산
정답 = 서울에서 대전까지 가장 빠른 경로 + 대전에서 부산까지 가장 빠른 경로 = 서울 -> 광명 -> 대전 -> 대구 -> 부산

메모이제이션(Memoization)

DP는 어려워보이지만 그냥 “기억하며 풀기”라고 생각하면 쉽다.

그러기 위해서 필수적으로 쓰이는 것이 “메모이제이션”이다.

위의 피보나치 수를 다시 보면, N번째 피보나치 수를 구한다고 가정해보자.

f(N)=f(N−1)+f(N−2)

f(N−1)=f(N−2)+f(N−3)

f(N−2)=f(N−3)+f(N−4)

...

f(2)=f(1)+f(0)

f(1)=1

f(0)=0

여기서, f(N) 을 구할 때, 사용 된 f(2) 의 값이나, f(N-1) 을 구할 때 사용 된 f(2) 의 값, f(N-2) 을 구할 때 사용 된 f(2) 의 값은 모두 같다.

이와 같이 각 문제에서 사용되는 부분문제가 겹치는 경우 같은 문제의 값을 매번 구하는 것은 비효율적이다. 이를 해결할 수 있는 방법이 메모이제이션(Memoization) 이다.

메모이제이션은 컴퓨터 프로그램이 동일한 계산을 반복해야 할 때, 이전에 계산한 값을 메모리에 저장함으로써 동일한 계산의 반복 수행을 제거하여 프로그램 실행 속도를 빠르게 하는 기술이다. 동적 계획법의 핵심이 되는 기술이다.

그래서 보통 DP문제는 메모이제이션을 하기위한 배열을 무조건 사용하는데 어려운 문제는 2차원 3차원 배열까지도 쓴다. 상태 값이 늘어나면 2차원, 3차원 배열이 되는 것이다.
보통 DP가 1차원 배열이면 index값만 들어가서 DP[index]이고
2차원이면 상태 값이 추가되서 DP[index][state] 처럼 사용되기도 하고,
DP[i][j] 처럼 i~j 범위 내의 값을 넣을 수도 있고, 당연하게도 문제마다 다르다.

결론적으로 메모이제이션을 위한 DP배열을 올바르게 정의내리는 것이 제일 중요하다.

※ 팁이 있다면 DP배열의 마지막값 DP[N]이 문제의 정답이 되도록 정의내리면 대부분의 문제가 풀리긴 한다.

구현

동적 계획법의 구현 방식에는 두 가지 방법이 있다.

Top-down 은 큰 문제를 작은 문제로 쪼개면서 풀어나가는 방식이다 ⇒ 재귀
Bottom-up 은 작은 문제부터 차례대로 풀어 나가는 방식이다. ⇒ for문

아래는 간단한 피보나치 문제 구현이다.

1. Top-down

public class Fibonacci {

    private int n;
    private int[] fibonacciMemory;

    public Fibonacci(int N){
        this.n = N;
        this.fibonacciMemory = new int[N + 1];
    }

    public int getFiboByTopdown(){
        return fibo(n);
    }

    private int fibo(int n) {
        if(n == 0) return 0;
        if(n == 1) return 1;
        if(fibonacciMemory[n] != 0) return fibonacciMemory[n];
        return fibo(n-1) + fibo(n-2);
    }
}

2. Bottom-up

public class Fibonacci {

    private int n;
    private int[] fibonacciMemory;

    public Fibonacci(int N){
        this.n = N;
        this.fibonacciMemory = new int[N + 1];
    }

    public int getFiboByBottomup(){
        if(n == 0) return 0;
        if(n == 1) return 1;

        fibonacciMemory[0] = 0;
        fibonacciMemory[1] = 1;
        for(int i = 2; i <= n; i++){
            fibonacciMemory[i] = fibonacciMemory[i-1] + fibonacciMemory[i-2];
        }
        return fibonacciMemory[n];
    }
}

➕ 그리디 알고리즘과 차이점

그리디 알고리즘은 현재 가능한 최선의 방법을 선택하여 문제를 해결하는 알고리즘이다. 그 순간의 최적의 해를 구할 수는 있지만 이 선택의 최종 결과도 “최적해”라는 보장은 없다.

Dijkstra(다익스트라), MST(최소 신장 트리) 등과 같이 최적해를 구할 수 있다는 것이 입증되어 있다면 DP보다 성능이 더 좋다.

그리디 알고리즘도 만족해야 하는 두 가지 특성이 있다.

탐욕 선택 속성(Greedy Choice Property) : 현재 선택이 이후의 선택에 영향을 주지 않는 경우
최적 부분 구조(Optimal Substructure) : 부분 문제들의 최적해를 모아 전체의 최적해를 구할 수 있는 경우

잘 보면 DP와 마찬가지로 최적 부분 구조 특성을 가지고 있다. 그래서 문제를 풀다보면 그리디와 비슷한 느낌을 받을 때가 있는데 이게 다 이런 이유에서이다.
그리디 알고리즘을 사용할 수 있을 것 같은데 “뭔가 부분 문제가 겹치는 것 같다”, “뭔가 다음의 선택에 영향을 주는 것 같다” 싶으면 DP 알고리즘이 적용되는 경우가 많다.

➕ 분할 정복과 차이점

동적계획법은 주어진 문제를 더 작은 문제들로 쪼갠 뒤 작은 문제의 답을 구하고, 그 답들로부터 주어진 문제를 구한다는 점에서 분할 정복(Divide & Conquer, D&C)와 비슷하다.

분할정복은 큰 문제를 해결하기가 어려워 단지 작은 문제로 나누어 푸는 방법이다. 여기서 가장 큰 차이점은 동적 계획법은 쪼개진 작은 문제가 중복되지만, 분할 정복은 중복되지 않는다는 점이다.

유형별 문제 추천

“부분 문제 반복”과 “최적 부분 구조”가 있는지 확인해서 DP가 가능한지 알아낼 수 있다. 하지만 코딩테스트를 보는데 이 문제가 부분 문제 반복이 있는지 최적 부분 구조가 있는지 확인하는 것이 쉽지는 않다.

그래서 DP를 잘 하기 위해서는 사실 개념보다도 유형을 좀 익히는 것이 중요하다. 즉, 다양한 유형의 문제를 많이 풀어봐야한다. 그래야 문제를 봤을 때 DP로 풀 수 있겠는데? 라는 발상이 떠오르기 때문이다. (DP는 발상이 떠오르는게 진짜 중요하다)

(최단 경로 문제 알고리즘인 다익스트라, 벨만-포드, 플로이드-워셜 알고리즘도 일종의 DP이지만 별개의 그래프 문제에 속한다고 생각하여 제외했습니다.)

동전 문제

동전 문제는 동전의 가치와 개수가 주어지고 원하는 값을 만드는 문제다.

동전의 개수가 무제한이면 쉽지만 개수가 주어지면 난이도가 올라간다.

살짝 그리디하고도 합쳐진 문제로 기본 풀이는 주어진 동전으로 만들 수 있는 가격을 DP 배열에 저장해주면 된다. 동전 간의 배수관계가 중요하다.

※ 예시 문제

동전 문제 G2 - 동전 개수, 동전 개수의 최솟값
동전 G3 - 동전 개수 정해져 있음, 사용하는 동전 개수를 최대로
동전2 G5 - 동전 무한대로 사용 가능, 사용하는 동전 개수를 최소로

누적합

이미 구해놓은 누적합을 이용해서 다음 누적합을 구할 수 있다.

1차원 누적합 공식 : S{i] = A[i] + S[i-1];

2차원 누적합 공식 : S[i][j] = A[i][j] + S[i-1][j] + S[i][j-1] - S[i-1][j-1];

차원이 늘어나면서 포함배제 개념이 들어간다.

대표적인 DP 유형의 문제이기에 2차원 누적합까지는 필수적으로 해둬야하고
3차원이나 대각선 누적합도 해보면 좋다. 기본 원리는 똑같기 때문에 더 어렵지도 않다.

※ 예시 문제

11660.구간 합 구하기 5 S1 - 2차원 누적합 기본 문제
25682.체스판 다시 칠하기 2 G4 - 2차원 누적합 살짝 응용
소형기관차 G3 - 누적합
2208.보석 줍기 G2 - 누적합
21757.나누기 G2 - 누적합
1028.다이아몬드 광산 P5 - 2차원 대각선 누적합

계단 수, 타일 채우기 (개수 세기)

점화식을 잘 세워서 풀어야 하는 문제

이전 상태에서 다음 상태로 가는 관계를 잘 파악해서 점화식을 세워주면 끝나는 문제지만
점화식을 못 세우면 못푼다.

※ 예시 문제

최소, 최대 비용 구하기

기본적으로 DP는 최소, 최대 비용(가치)를 구하는 문제에서 자주 쓰인다.

보통 이런 문제들이 부분 문제가 반복되고 최적 부분 구조로 되어있어서 잘 파악해서 DP배열 만들어서 저장해주면 된다.

※ 예시 문제

파일 합치기 G3 - 최소 비용 구하기

로봇 조종하기 G2 - 최대 가치

비트 마스킹 (비트필드)

DP배열을 비트마스킹을 활용하여 선언해주는 알고리즘이다.

DP배열에 비트값이 들어가서 수 하나로 여러 상태(비트)를 가지고 있을 수 있다.

예를 들어 DP[1024] 배열을 선언했다고 치면 1024 =2^10으로 10비트를 가지고 있으므로 10개의 상태를 들고 있는 것이다. 즉, 10차원 배열처럼 사용할 수 있다.
Long 자료형의 경우 64비트이므로 최대 64비트까지만 만들 수 있다는 한계점이 존재한다.

이런 배열을 비트필드라고 하고 이런 비트필드를 사용해야 하는 DP 문제들이 있다.

※ 예시 문제

1562.계단 수 G1 - 비트필드
1311.할 일 정하기 G1 - 비트필드
2098. 외판원 순회 G1 - 비트필드

KnapSack 알고리즘 (배낭 문제)

https://howudong.tistory.com/106

dp [K][W] = max(dp[K-1][W], K가치 + dp[K-1][W-K무게])
위 점화식처럼 dp[k][*]가 dp[k-1][*]에만 의존하는 경우 차원 하나를 줄일 수 있다.

⇒ dp[w] = max(dp[w], 가치+dp[w-무게])

하지만 이 경우 w를 0부터가 아니라 k부터 반대로 갱신해야 한다.

0부터 갱신해버리면 이미 갱신한 (w-무게)번째 값을 이용해 또 갱신을 해버리므로 안된다.

시간복잡도 = O(NK)

핵심 알고리즘 코드

// k: 가방(1개)이 담을 수 있는 최대 무게
for (int i = 0; i < n; i++) {
	for (int j = k; j >= w[i]; j--) {
		dp[j] = max(dp[j], dp[j - w[i]] + v[i]);
	}
*}*

전체 코드

import java.io.*;
import java.util.*;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());
    	int n = Integer.parseInt(st.nextToken());
    	int k = Integer.parseInt(st.nextToken());
    	int[] dp = new int[k+1];
    	int[] w = new int[n];
    	int[] v = new int[n];
    	for (int i = 0; i < n; i++) {
    		st = new StringTokenizer(br.readLine());
    		w[i] = Integer.parseInt(st.nextToken());
    		v[i] = Integer.parseInt(st.nextToken());
    	}
    	for (int i = 0; i < n; i++) {
    		for (int j = k; j >= w[i]; j--) {
    			dp[j] = Math.max(dp[j], dp[j - w[i]] + v[i]);
    		}
    	}
    	System.out.println(dp[k]);
	}
}