[세그먼트 트리] Lazy propagation (구간 합 구하기 2, C++)

beegle·2025년 2월 23일

자료구조&알고리즘

목록 보기

4/6

Lazy Propagation이란?

Lazy Propagation 알고리즘은 한국말로는 “느리게 갱신되는 세그먼트 트리”라고 불리는데요, 세그먼트 트리의 응용 알고리즘 중 하나입니다. 말 그대로 게으르게(Lazy) 전파(Propagation)한다는 의미를 가지고 있습니다. 게으르다는건 일을 미룬다는 뜻이고, 그 뜻대로 이 알고리즘 발상의 근본은 “업데이트를 미룬다” 라는 점에서 시작됩니다. 필요할 때에만 업데이트를 하고 필요하지 않은 업데이트는 모아두었다가 한 번에 하는 것이죠.

그럼 언제 쓸까?

이 알고리즘은 위에서 말씀 드렸다싶이 세그먼트 트리의 응용 알고리즘 중 하나이기 때문에, 기본적으로 세그먼트 트리를 사용하는 문제에서 사용됩니다. 그렇기 때문에 어떠한 구간 쿼리를 필요로 하는 문제에서 많이 쓰입니다.

근데 위에서 “업데이트”를 미루는 알고리즘이라고 말씀 드렸었죠? 그렇다면 당연하게도 업데이트가 자주 발생하는 문제에서 사용할 것이라고 짐작할 수 있을겁니다. 이 알고리즘은 그 중에서도 “구간 갱신”이 자주 일어나는 문제에서 사용하는 알고리즘입니다.

원리

void update_range(int node, int start, int end, int left, int right, long long diff) {
    if (left > end || right < start) {
        return;
    }
    if (start == end) {
        tree[node] += diff;
        return;
    }
    update_range(node*2, start, (start+end)/2, left, right, diff);
    update_range(node*2+1, (start+end)/2+1, end, left, right, diff);
    tree[node] = tree[node*2] + tree[node*2+1];
}

위는 구간 갱신을 해야할 경우 기존 세그먼트 트리의 업데이트 코드입니다.

left~right번째 수에 diff를 더하는 코드입니다. node 하나하나 diff를 더해주는 방식이죠.

만약 범위가 start~end라면 모든 수를 전부 변경해줘야 하므로 시간복잡도는 O(NlogN)이 됩니다. 만약 이런 갱신이 M번 발생한다면? 시간복잡도는 O(NMlogN)으로 M에 따라 다르겠지만 시간 초과가 날 확률이 높아 보입니다. 이럴 경우 구간 갱신을 효율적으로 처리해주는 알고리즘이 Lazy Propagation 알고리즘입니다.

원리를 먼저 간단하게 설명하자면,

구간 갱신을 할 때 갱신을 자식 노드 하나나하 전부 찾아가서 해주는 것이 아니라 부모 노드만 업데이트 해주고 lazy배열에 따로 저장을 해둠으로써 나중에 자식노드를 갈 일이 생긴다면 그 때 lazy배열을 확인하여 추가로 업데이트 해주는 방식입니다.

그래서 항상 lazy배열에 값이 0이 아닌지 확인하고, 0이 아니라면 추가로 업데이트 해줘야할 것이 있다는 뜻이므로 노드에 값을 추가로 더해주고, 자식 노드에 lazy값을 물려줍니다.

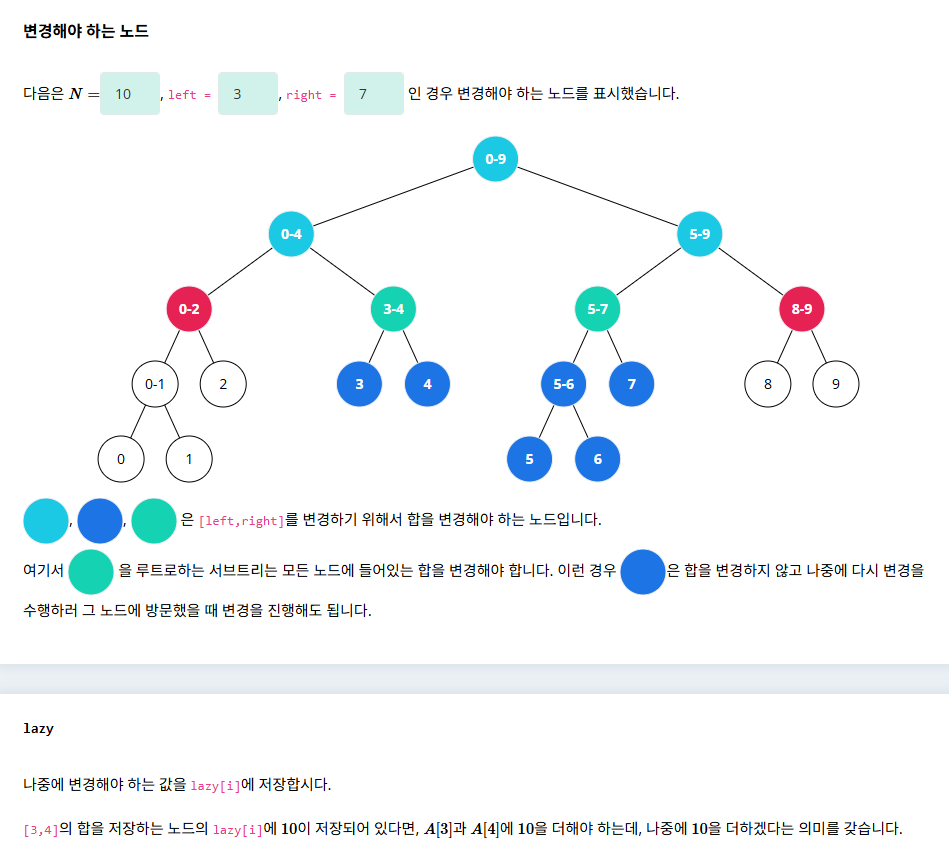
[3,7] 범위를 갱신하는 경우를 예시로 들어보겠습니다.

[0,9], [0,4], [5,9] 범위의 노드처럼 [3,7]보다 크거나 부분만 포함하는 경우는 갱신해야 하는 노드와 갱신하지 말아야 하는 노드가 섞여 있기 때문에 부모 노드만 업데이트할 수가 없습니다. 그렇기 때문에 lazy 전략을 사용하지 못하고 자식노드로 이동해야 합니다.

[3,4], [5,7] 범위의 노드는 [3,7] 범위에 모두 포함됩니다. 이 경우는 부모 노드만 갱신해두고 자식노드는 나중에 필요할 때 갱신할 수 있도록 lazy배열에 저장합니다.

그러면 lazy배열에는 갱신하려는 값인 diff 만큼만 갱신해주면 될 것 같은데, [3,4] 노드와 같은 부모 노드인 값 tree[node] 값은 어떻게 갱신해줘야 할까요? 직감적으로도 diff 만큼만 바꿔주면 안되겠죠?

범위가 [3,4]인 노드가 가지는 값의 뜻은 3~4 범위의 노드값의 “합”입니다. 그렇기에 diff가 아니라 갱신하는 범위 * diff 만큼 더해줘야 합니다.

tree[node] += (end-start+1) * diff

구현

구현 예시 코드는 백준의 구간 합 구하기 2 문제 코드입니다.

init

기본 세그먼트 트리 코드와 똑같습니다.

typedef long long ll;

ll init(int node, int start, int end){
    if(start == end){
        return tree[node] = arr[start];
    }
    return tree[node] = init(node*2, start, (start+end)/2)
        + init(node*2+1,(start+end)/2+1, end);
}

update

update 함수는 update_lazy함수와 update_range함수로 나뉘어집니다.

update_lazy함수는 lazy값이 있는지 확인한 후 업데이트하고 자식 노드에게 물려주는 역할을 합니다.

update_range함수는 기존 update함수와 비슷한 역할로 원하는 범위의 값을 업데이트 해주는 역할을 합니다.

void update_lazy(int node, int start, int end){
    if(lazy[node] != 0){ //lazy 값이 있으니까 추가로 업데이트 해야한다.
        tree[node] += (end-start+1) * lazy[node]; // 범위 * diff 만큼 더해준다.
        if(start != end){ // 자식에게 물려준다.
            lazy[node*2] += lazy[node];
            lazy[node*2+1] += lazy[node];
        }
        lazy[node] = 0; // 업데이트 완료
    }
}

void update_range(int node, int start, int end, int left, int right, ll diff){
    update_lazy(node, start, end); // 항상 lazy값이 있는지 확인

    if(left>end || right<start){ // 범위 초과
        return;
    }
    if(left<=start && end<=right){ // 범위 포함, lazy 전략으로 부모만 갱신 후 lazy값 저장
        tree[node] += (end-start+1) * diff;
        if(start!=end){
            lazy[node*2] += diff;
            lazy[node*2+1] += diff;
        }
        return;
    }
    update_range(node*2, start, (start+end)/2, left, right, diff);
    update_range(node*2+1, (start+end)/2+1, end, left, right, diff);
    tree[node] = tree[node*2] + tree[node*2+1];
}

sum

sum함수는 기존 sum함수에 update_lazy함수만 추가로 호출해주면 됩니다.

ll sum(int node, int start, int end, int left, int right){
    update_lazy(node,start,end);
    if(left > end || right < start) return 0;
    if(left <= start && right >= end){
        return tree[node];
    }
    return sum(node*2, start, (start+end)/2, left, right)
        + sum(node*2+1, (start+end)/2+1, end, left, right);
}

전체 코드

#include <bits/stdc++.h>

using namespace std;

typedef long long ll;
typedef vector<ll> vll;
typedef vector<int> vi;

const int N = 1001000; 
int n,m,k; 

vll tree, arr,lazy;

ll init(int node, int start, int end){
    if(start == end){
        return tree[node] = arr[start];
    }
    return tree[node] = init(node*2, start, (start+end)/2)
        + init(node*2+1,(start+end)/2+1, end);
}
void update_lazy(int node, int start, int end){
    if(lazy[node] != 0){ 
        tree[node] += (end-start+1) * lazy[node]; 
        if(start != end){ 
            lazy[node*2] += lazy[node];
            lazy[node*2+1] += lazy[node];
        }
        lazy[node] = 0;
    }
}

void update_range(int node, int start, int end, int left, int right, ll diff){
    update_lazy(node, start, end);

    if(left>end || right<start){ 
        return;
    }
    if(left<=start && end<=right){ 
        tree[node] += (end-start+1) * diff;
        if(start!=end){
            lazy[node*2] += diff;
            lazy[node*2+1] += diff;
        }
        return;
    }
    update_range(node*2, start, (start+end)/2, left, right, diff);
    update_range(node*2+1, (start+end)/2+1, end, left, right, diff);
    tree[node] = tree[node*2] + tree[node*2+1];
}
ll sum(int node, int start, int end, int left, int right){
    update_lazy(node,start,end);
    if(left > end || right < start) return 0;
    if(left <= start && right >= end){
        return tree[node];
    }
    return sum(node*2, start, (start+end)/2, left, right)
        + sum(node*2+1, (start+end)/2+1, end, left, right);
}

int main(){
    ios::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);

    cin >> n >> m >> k ;

    arr = vll(n+10);
    tree = vll(4*(n+10));
    lazy = vll(4*(n+10));
    
    
    for(int i=1;i<=n;i++){
        cin >> arr[i];
    }
    init(1,1,n);
    for(int i=0;i<m+k;i++){
        int a,b,c;
        cin >> a >> b >> c;
        if(a==1){// add
            ll d; cin >> d;
            update_range(1,1,n,b,c,d);
        }
        else{// sum
            cout << sum(1,1,n,b,c) <<'\n';
        }
    }
    
    return 0;
}