구간 합 알고리즘 (2차원 배열)

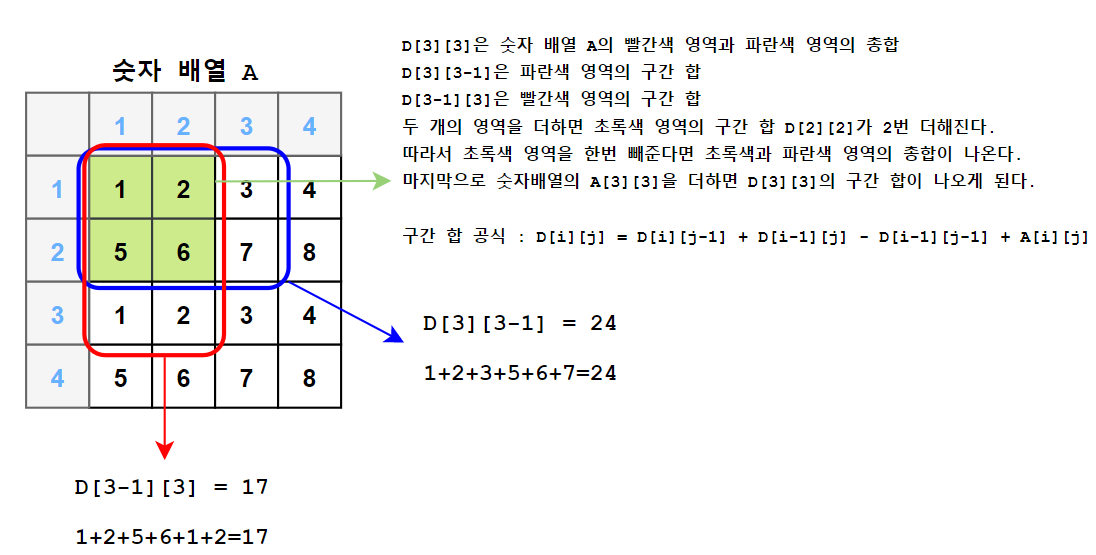
2차원 배열의 값을 채우는 구간 합 공식

만들어본 코드

public class PrefixSum2_example {
    public static void main(String[] args){
        int[][] A = {
            {0, 0, 0, 0, 0},
            {0, 1, 2, 3, 4},
            {0, 5, 6, 7, 8},
            {0, 1, 2, 3, 4},
            {0, 5, 6, 7, 8}
        };

        System.out.println("숫자 배열 A");
        for(int i = 0; i < A.length; i++) {
            for(int j = 0; j < A.length; j++) {
                System.out.print(A[i][j] + " ");
            }
            System.out.println();
        }

        int[][] D = new int[A.length][A.length];
        // 구간 합 배열 채우기
        for(int i = 1; i < A.length; i++) {
            for(int j = 1; j < A.length; j++) {
                D[i][j] = D[i][j-1] + D[i-1][j] - D[i-1][j-1] + A[i][j];
            }
        }

        System.out.println("\n구간 합 배열 D");
        for(int i = 0; i < D.length; i++) {
            for(int j = 0; j < D.length; j++) {
                System.out.print(D[i][j] + " ");
            }
            System.out.println();
        }
    }
}

실행 결과

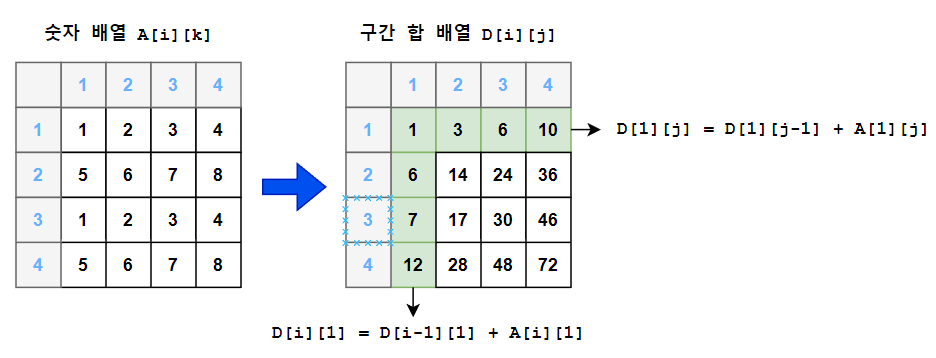
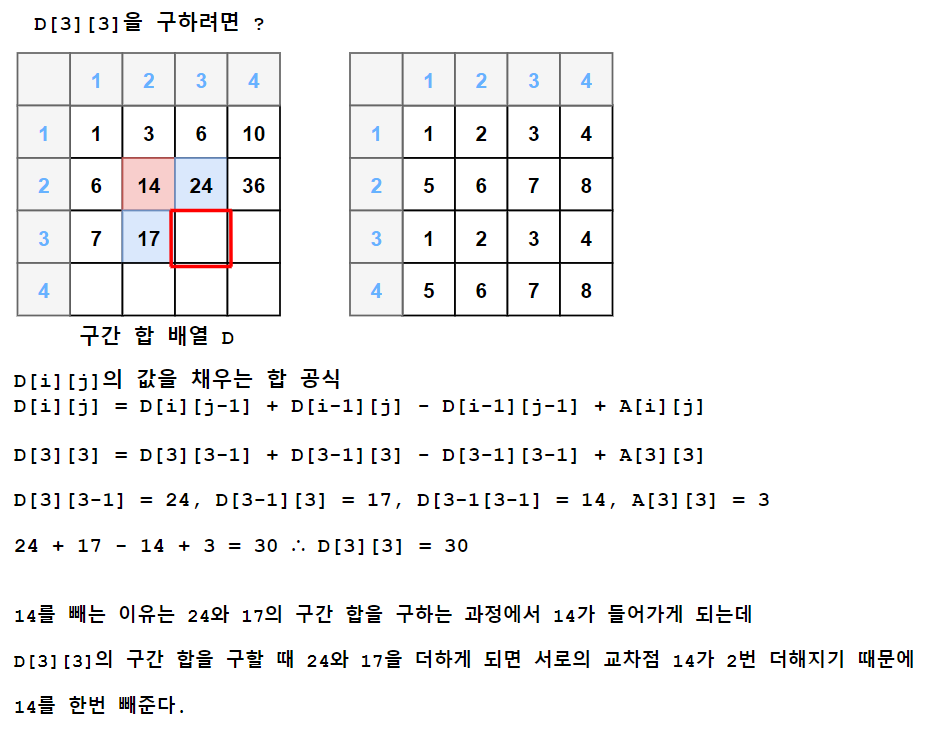
D[i][j]를 채우는 구간 합 공식
D[i][j] = D[i][j-1] + D[i-1][j] - D[i-1][j-1] + A[i][j]를 할 때
0이 없다면 위 공식에서 약간 변형을 해야하고 기존 0의 공간이 없어지면 해당 영역들을 모두 예외처리 시켜야한다.

단, 꼭 0을 넣어주지 않아도 된다. 하지만 나는 0으로 채워 넣게 되면 예외처리나 코드 자체가 간단해지기 때문에 넣게 되었다.

---

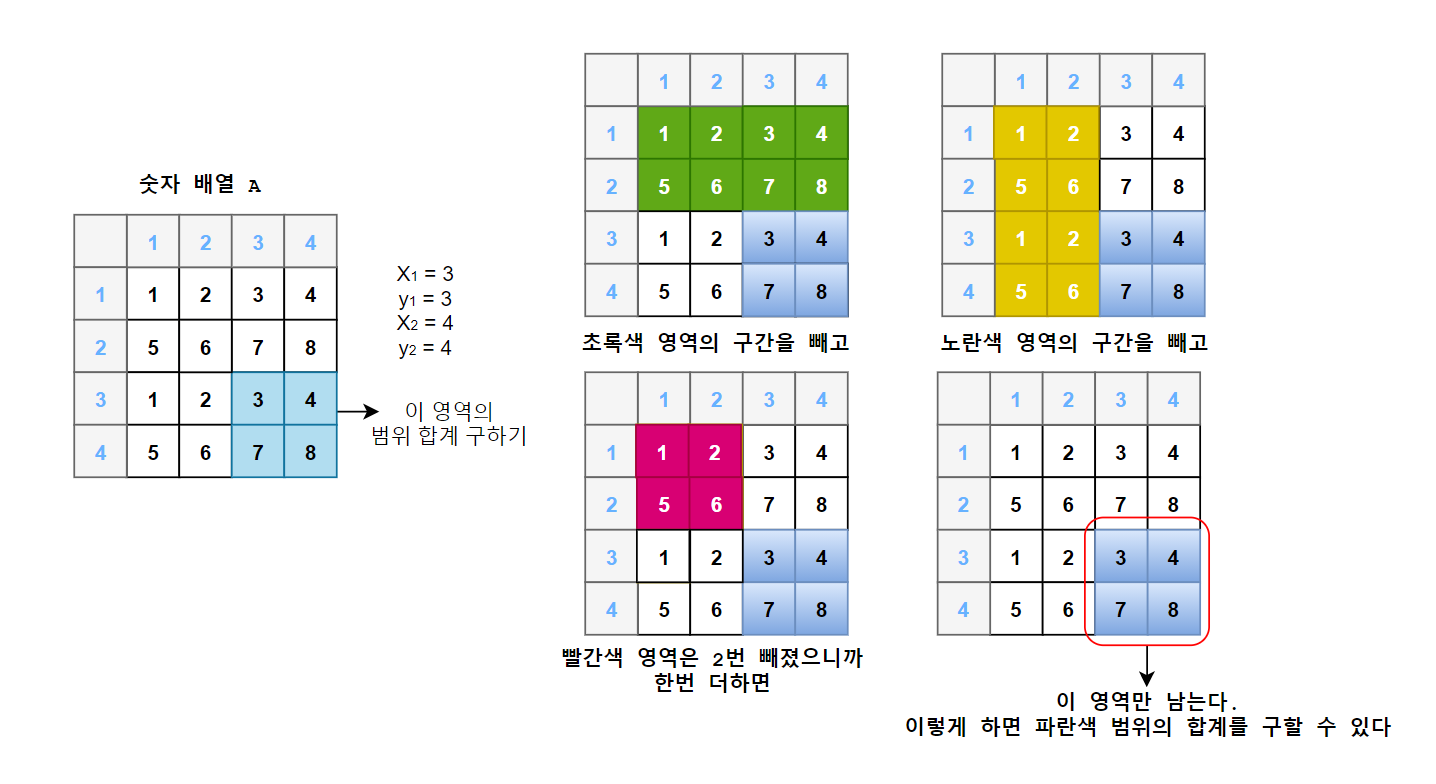
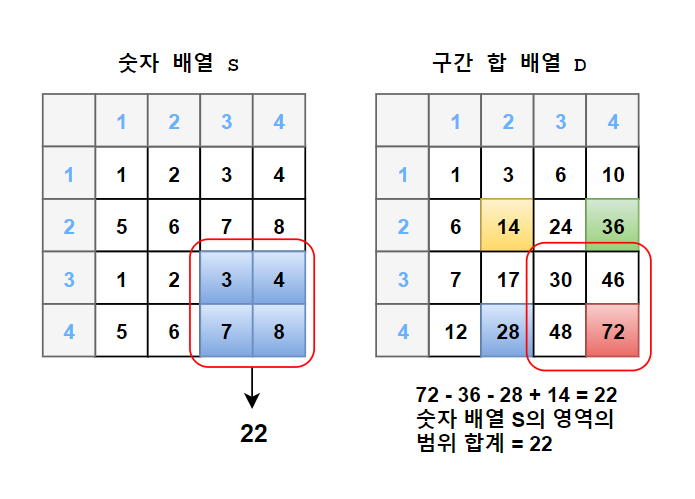
숫자배열 A의 지정된 영역의 범위 합계 구하기

구간 합 배열을 이용해 지정된 영역의 범위 합계 구하기 ?
1. 구하고자 하는 영역의 구간 합 D[4][4]에서
2. 초록색 영역의 영역의 총합은 구간 합 배열에서 D[4][2]를 빼고
3. 노란색 영역의 영역의 총합은 구간 합 배열에서 D[2][4]를 빼고
4. 그리고 중복되서 빠진 빨간색 영역의 구간 합 배열 D[2][2]를 한번 더 더해준다면
--> 숫자 배열 A의 파란색 범위의 합계를 구할 수 있다.
--> 공식 D[x2][y2] - D[x2][y1-1] - D[x1-1][y2] + D[x1-1][y1-1];