🪄 Definition
- A random variable X(u) is a mapping from the sample space to the real line.
In other words, an assginment of a number to every possible outcomes.
X(u):U→R
⭐ We can have several random variables defined on the same sample space
- Discrete RV
X(fi)=10i, in die experiment
X∈{10,20,30,40,50,60} ~ Discrete RV
- case1 f2=f3=20 is okay.
- case2 f2=20,f2=30 is not function.
- Continuous RV
U=(0,12], X(u)=u2, X∈(0,144] ~ Continuous RV 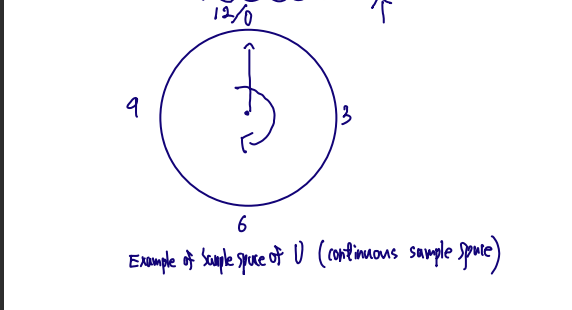
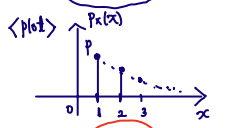
■ Probability Mass Function a.k.a. PMF
- X(u)→ When we define the RV, describe what kind of experiment it was.
In PMF, we describe the RV, all we have to give is Probability.
PX(x)=P{X=x}, each of elements have probability
- X: Random Variable
- x: Any number of set
📙Note
- PX(x)≥0
- ∑i=xPX(x)=1
■ Probability Density Function a.k.a. PDF
- A continuous RV X is described by a probability density function, fX(x)
- −∞∫∞fX(x) dx=1
- b∫afX(x) dx=P[a≤x≤b]
- P(X∈B)=B∫fx(x) dx
- P(X≤X≤x+δ)=x∫x+δfX(x) dx
If δ is very small, δ=0→ P(X=x)
■ Probability Distribution Function (Cumulative Distribution Function, a.k.a. CDF)
FX(x)=P[X≤x]=−∞∫xfX(θ) dθfX(x)=dxdFx(x)→ Find to the density function using the CDF

■ Properties of Probability Distribution Function
- FX(∞)=P[X≤∞]=1
FX(−∞)=P[X≤−∞]=0
- FX(x) is a non-decreasig function of x
In other words, if x1<x2, then FX(x1)≤FX(x2)
- P[X>x]=1−FX(x)
- FX(x) is right-continuous
- P[x1<X≤x2]=FX(x2)−FX(x1)
- Proof ) {X≤x2}={x1<X≤x2}⋃{X≤x1} P{X≤x2}=P{x1<X≤x2}+P{X≤x1} (∵ 상호배반) FX(x2)=P{x1<X≤x2}+FX(x1) ∴P[x1<X≤x2]=FX(x2)−FX(x1)
- P[X=x]=P[x−<X≤x]=FX(x)−FX(x−)

✏️ Example
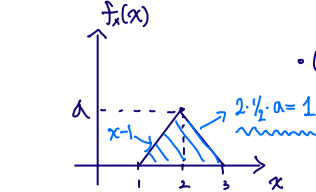
Question. What is the FX(x)= ?
According to the definition, FX(x)=−∞∫xfx(θ) dθ
Then,
- x<1→Fx(x)=0
- 1≤x<2→Fx(x)=1∫x(θ−1) dθ=2x2−x+21
- 2≤x<3→FX(x)=21+2∫x(3−θ) dθ=2−x2+3x−27
- x≥3→FX(x)=1
■ Typical Density Function
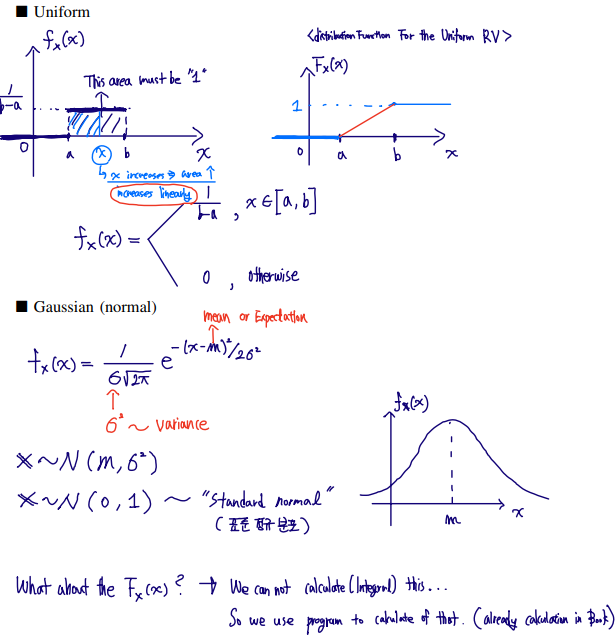
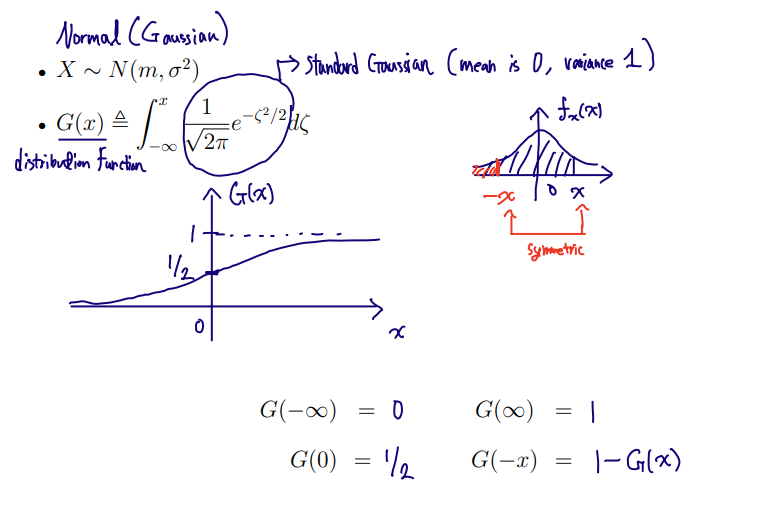
- Q(x)=1−G(x)
✏️ Example
- Let's suppose that X ~ (−3,22)
P[∣X+3∣<2]=P{−5≤X≤−1}
⇔FX(−1)−FX(−5)⇔G(2−1+3)−G(2−5+3)⇔G(1)−G(−1)⇔G(1)−(1−G(1))⇔2×G(1)−1∴1−2×Q(1)
■ Exponential
fX(x) of Exponential
- λ×e−λx, x≥0
- 0, otherwise
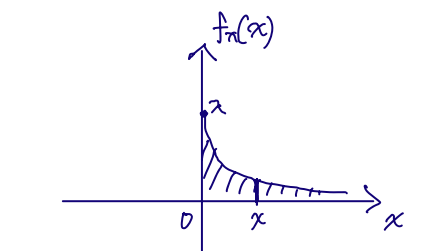
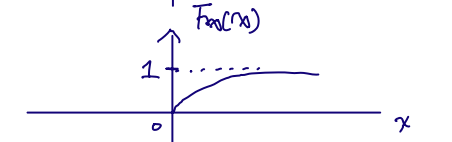
FX(x)=0∫xλe−λθ dθ
=[−e−λθ]0x
=1−eλx, x≥0
■ Poisson

- PX(k)= (kn)×pk×qn−k, At that time (p=Tτ,q=1−Tτ)
- Assume T→∞, n→∞, while n/T→λ
(n/T means that "expected number of points in length 1")
- PX(k)≃e−λτ×k!(λτ)k ~ Poission RV
🪄 Question : What is the density of distance between adjacent points?
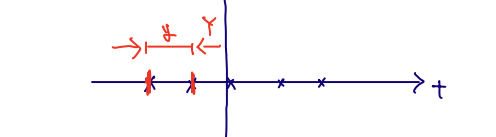
FY(y)=P[Y≤y]
⇔P[Y>y]=P{ No Point in Interval with Length y }
⇔1−FY(y)=e−λy
⇔FY(y)=1−e−λy
∴fY(y)=λ×e−λy, y≥0
본 글은 HGU 2023-2 확률변수론 이준용 교수님의 수업 필기 내용을 요약한 글입니다.