신장트리(Spanning Tree)

신장트리의 정의

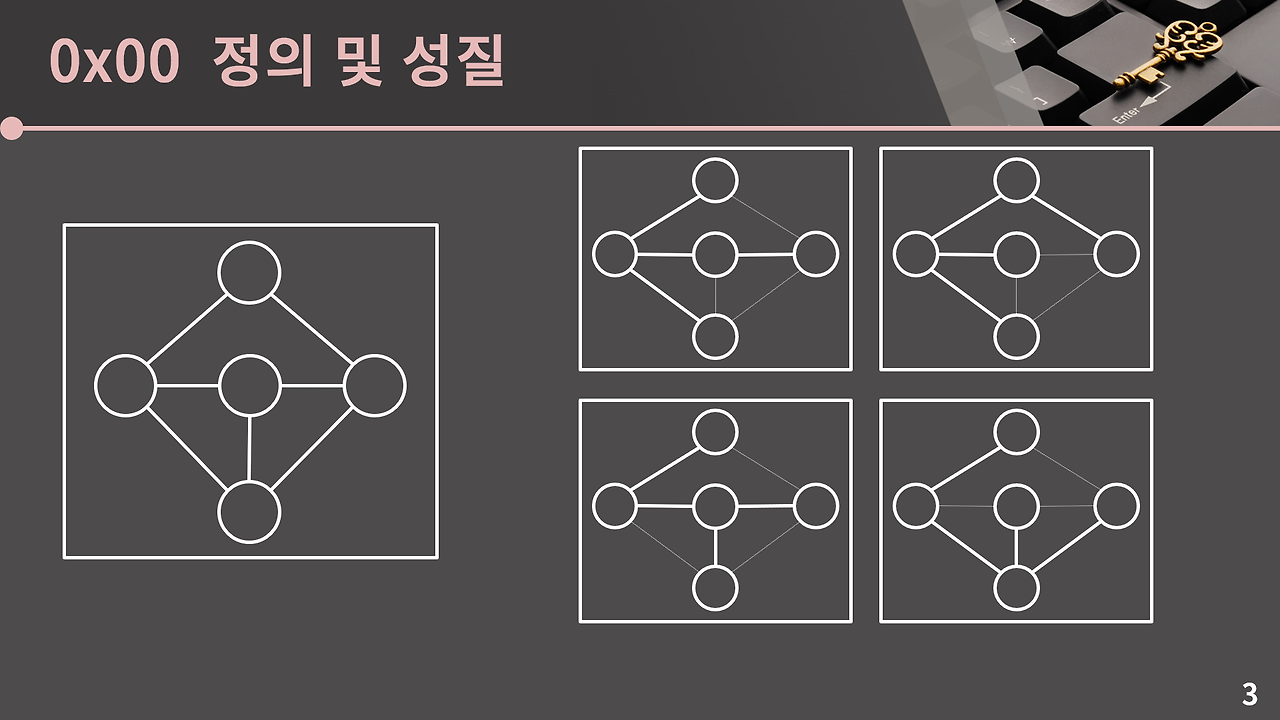
신장트리는 그래프 내의 모든 노드를 포함하면서 사이클이 없는 부분 그래프를 신장트리라고 한다.

트리의 성질로부터 주어진 그래프의 정점이 V개일 때 신장 트리는 V-1개의 간선을 가지고 있음을 알 수 있습니다.

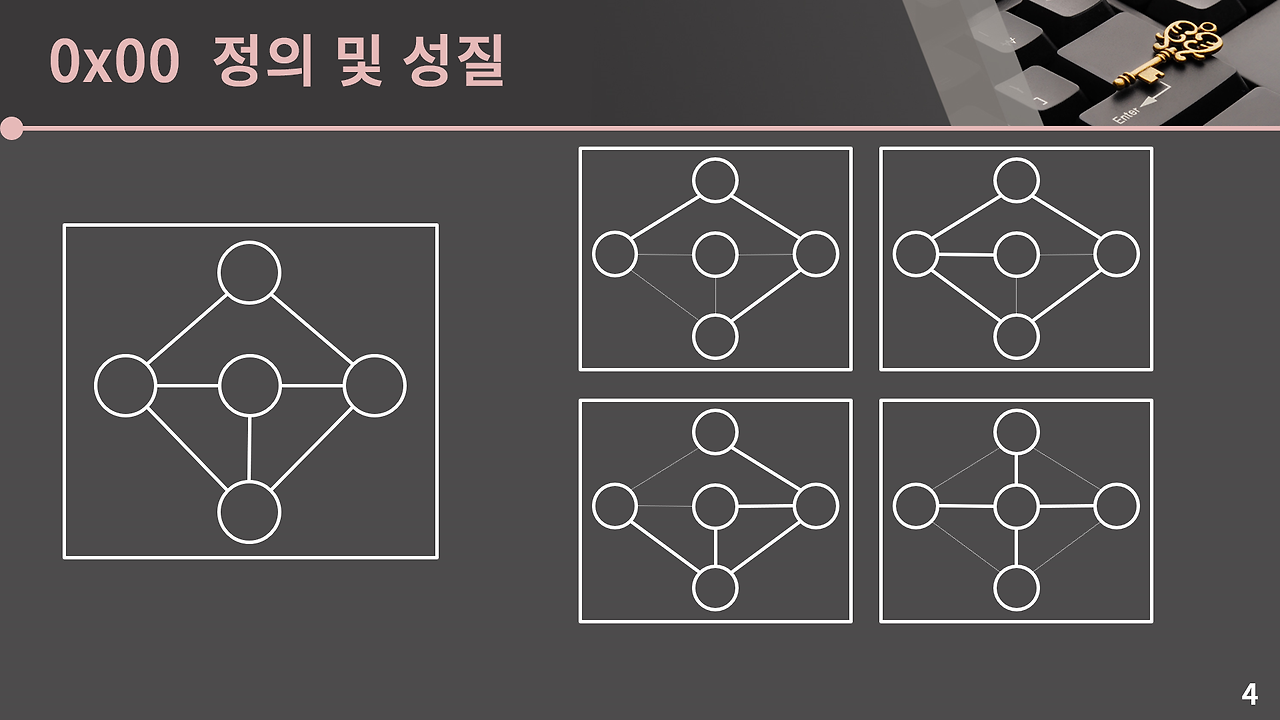
위에서의 오른쪽에 있는 그래프들은 간선이 없는 노드가 있다던가, 사이클이 있는 그래프, 혹은 원래 없던 간선들이 있는 그래프로 신장트리의 예가 아니다.

최소신장트리

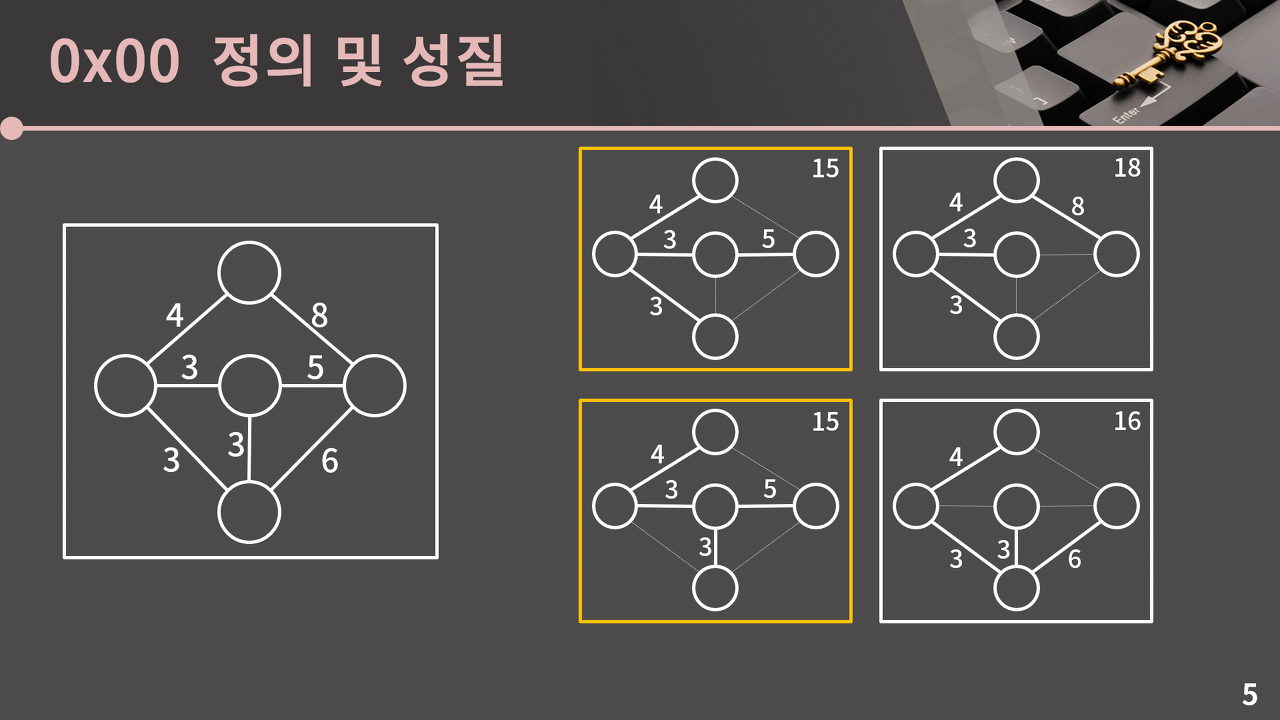
최소신장트리는 신장트리 중에서 간선의 합이 최소인 신장트리를 의미한다.
위에서 간선의 합이 15인 트리가 최소신장트리이고, 사진을 보면 알 수 있듯이 최소신장트리는 무조건 한개가 아니다.

최소신장트리 알고리즘

크루스칼 알고리즘과 프림알고리즘은 그리디 알고리즘을 기반으로 최소 신장 트리를 구하는 알고리즘이다.

크루스칼 알고리즘(Kruskal)

크루스칼 알고리즘은 쉽게 요약을 하면 가장 비용이 낮은 간선부터 시작해 간선을 크기 순으로 살펴보며 서로 떨어져 있던 정점들을 합쳐나가서 총 V-1개의 간선을 택하는 알고리즘이다.

하지만 무작정 작은 가중치의 간선을 구하다 보면 사이클을 형성하는 그래프가 될 수 있으므로 유의해야 한다.

하지만 Union Find알고리즘을 알고 있어야 하므로 상세 설명은 우선 생략한다.

프림 알고리즘(Prim)

간선을 중심으로 최소신장트리를 구하는 크루스칼 알고리즘과 달리 노드를 중심으로 최소신장트리를 구하는 알고리즘이다.

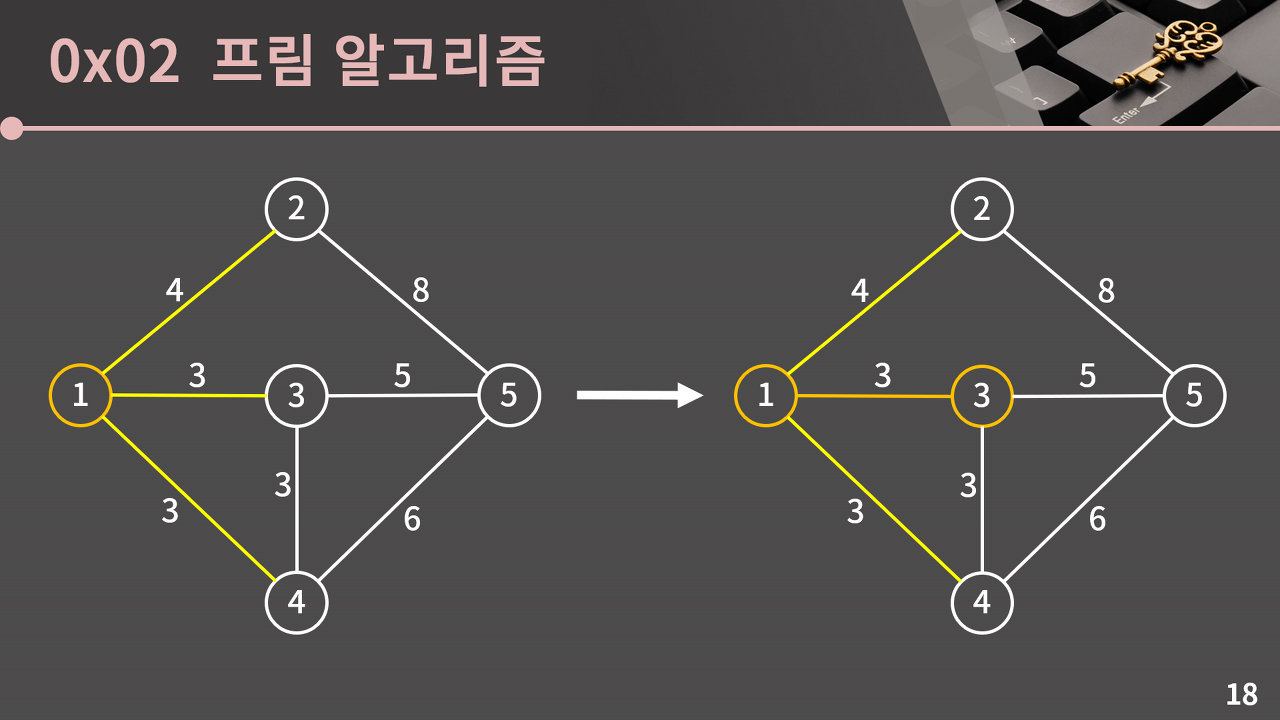
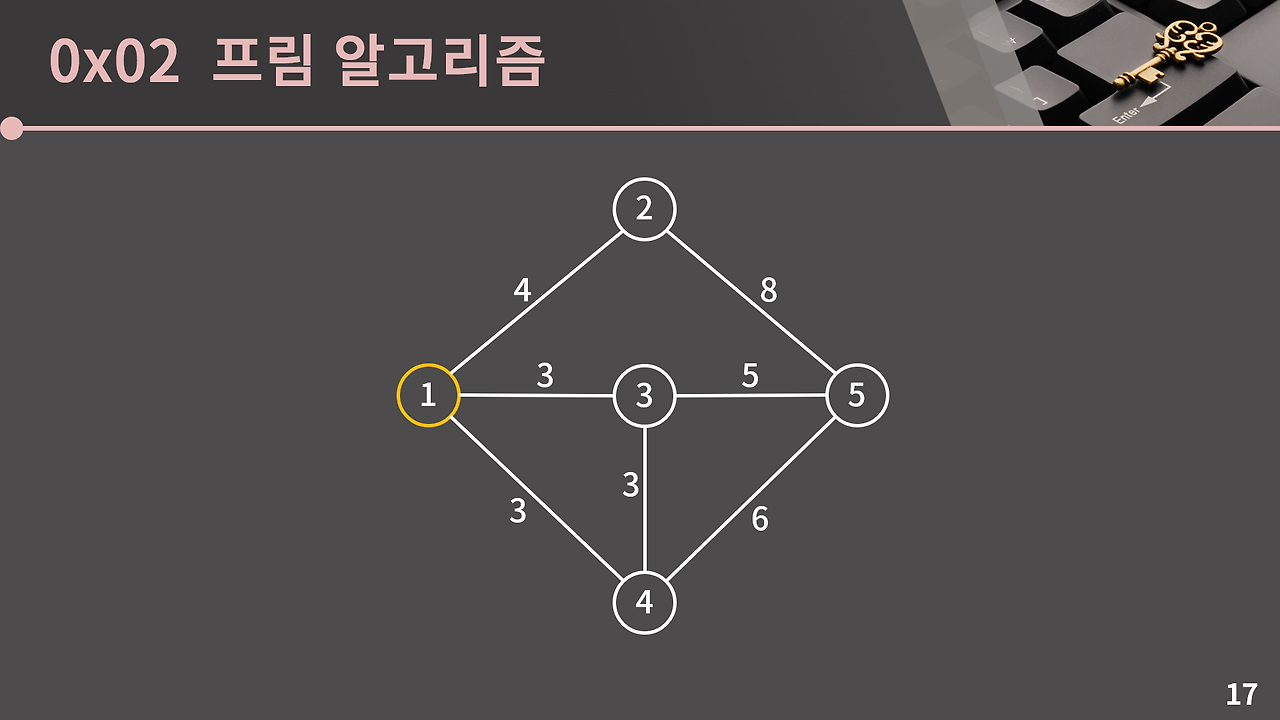
임의의 정점 1을 선택해 최소 신장 트리에 넣는다.

임의의 정점 1과 연결 된 노드 중에서 최소 신장트리에 들어가지 않은 2,3,4중 가중치가 낮은 3과 4중에서 임의로 3을 선택하여 최소 신장 트리에 추가한다.

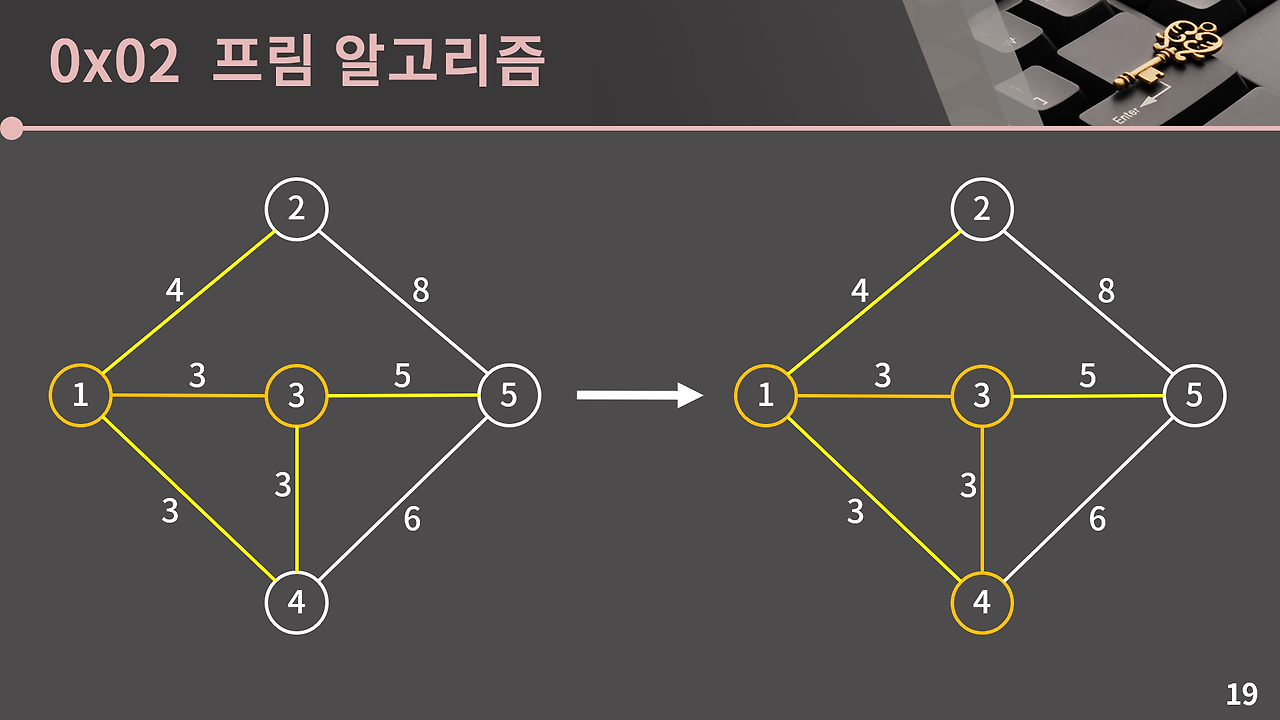
현재 최소 신장 트리에 포함된 정점과 포함되지 않은 정점을 연결하는 간선은 1과 2, 3과 5, 3과 4, 1과 4의 네개가 있고, 이 중 가중치가 낮은 3과4, 1과 4의 간선 중 임의로 3과 4를 잇는 간선을 선택하고, 최소 신장트리에 4를 추가한다.

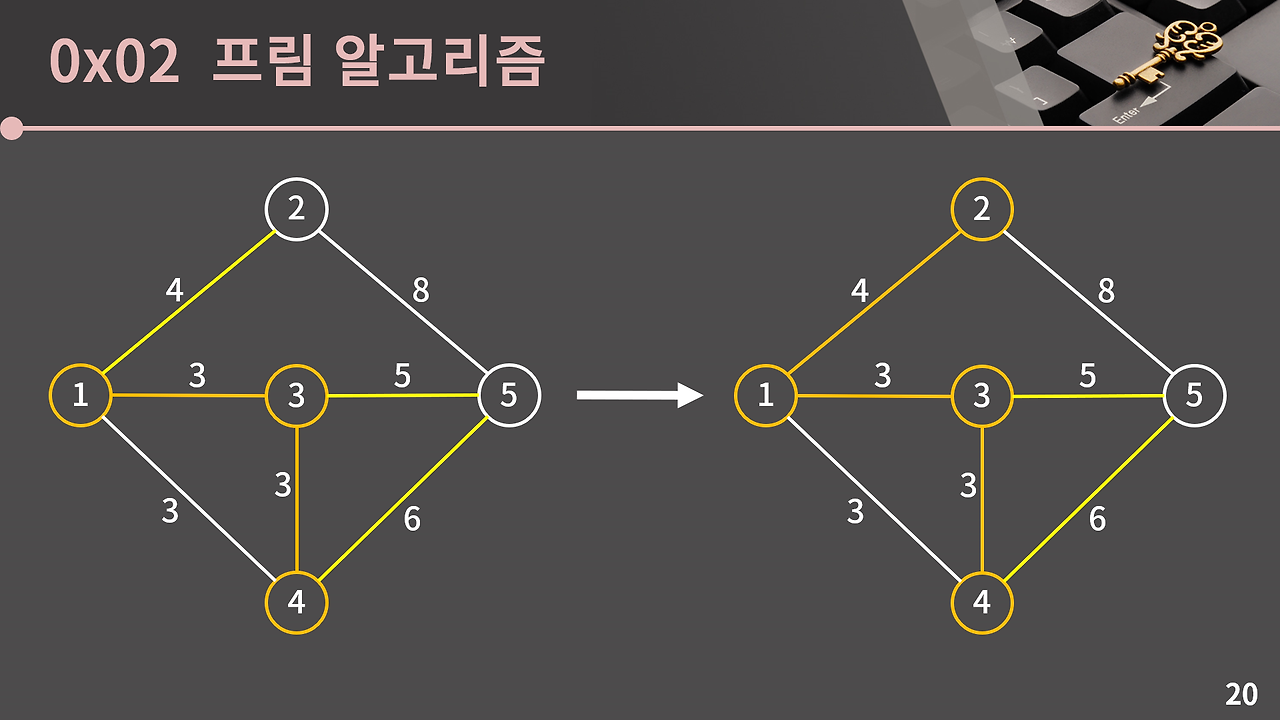
이번엔 1과 2, 3과 5, 4와 5를 연결하는 간선 중 1과 2를 연결하는 간선을 선택하고 최소 신장 트리에 2를 추가한다.

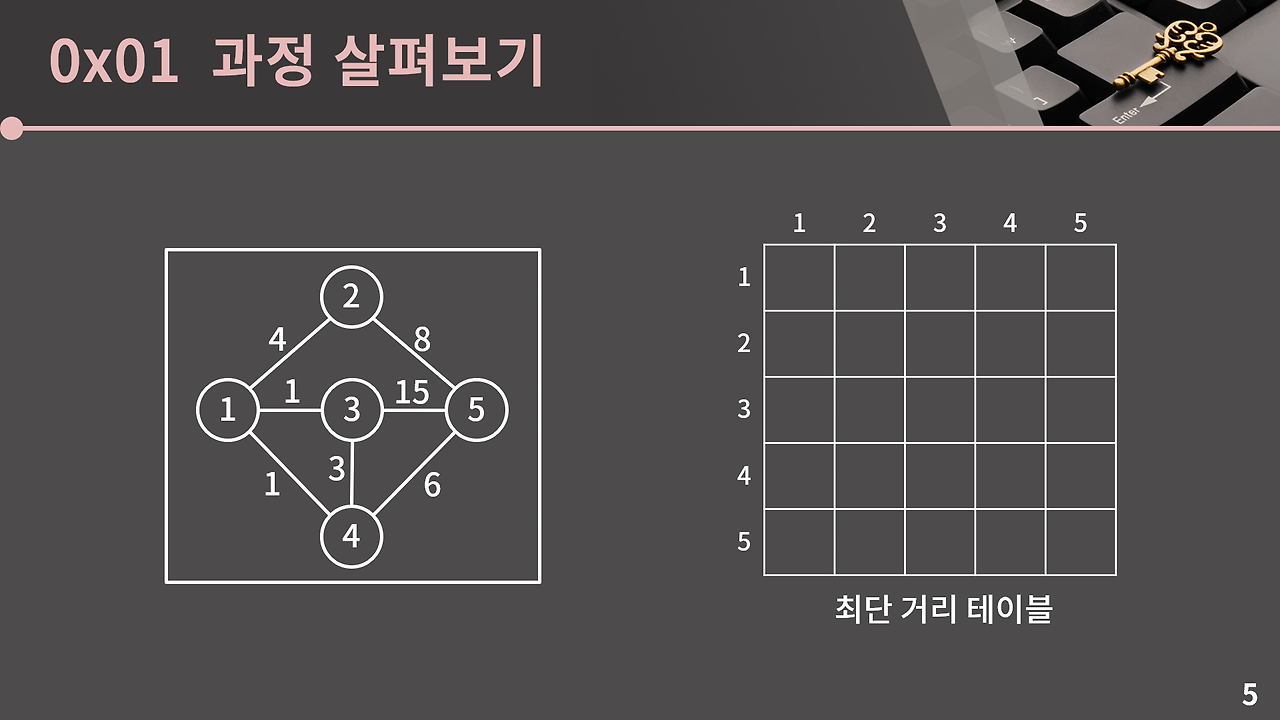
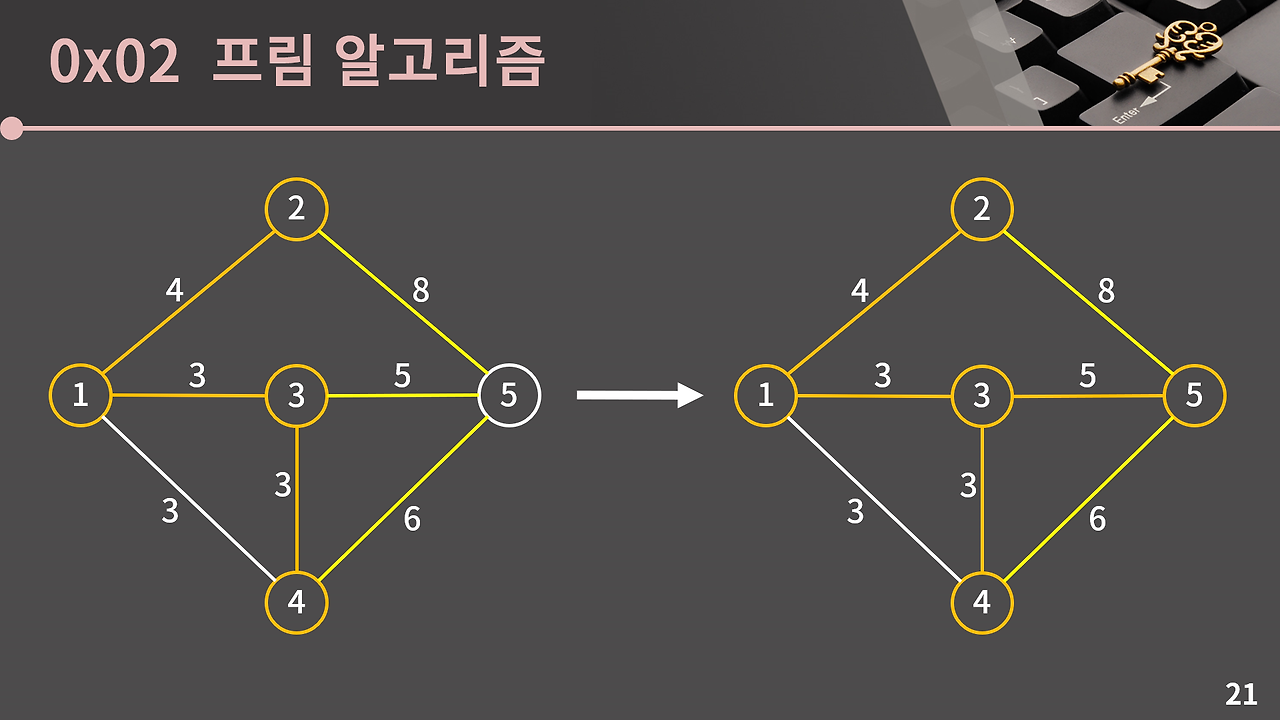
마지막으로 3과 5의 간선을 선택하고, 최소 신장 트리에 5을 추가하고, 최소 신장 트리를 만들어내는데 성공한다.

프림 알고리즘 구현

프림 알고리즘을 구현 할 때에는 매번 최소인 간선을 선택하고, 선택할 수 있는 간선이 늘어 나는 경우가 있다. 이런 경우에는 우선 순위 큐를 사용해서 구현 할 수 있다.

import heapq

def prim(graph, start):
    mst = []  # 결과 트리
    visited = set() # 방문 여부를 저장하는 집합
    edges = []  # 우선순위 큐
    count = 0
    cost = 0

    # 시작 노드를 우선순위 큐에 추가
    heapq.heappush(edges, (0, start))

    # 이동 가능한 노드가 없거나 모든 노드를 방문하여 이용한 간선의 갯수가 v - 1이 될때까지 반복
    while edges and count < len(graph) - 1:
        # 가장 가중치가 작은 에지를 선택
        w, node = heapq.heappop(edges)

        # 이미 방문한 노드는 건너뛴다.
        if node not in visited:
            cost += w
            count += 1
            # 방문하지 않은 노드라면 결과 트리에 추가
            visited.add(node)
            mst.append((node, w))
            # 현재 노드와 연결된 에지를 우선순위 큐에 추가
            for edge, w in graph[node].items():
                heapq.heappush(edges, (w, edge))
    # 고립 노드 존재시 모두 연결할 수 없으므로 체크
    if count == len(graph) - 1:
        return mst, cost
    return False

if __name__ == "__main__":
    # 그래프 정의 (노드와 가중치)
    graph = {
        'A': {'B': 1, 'C': 4},
        'B': {'A': 1, 'C': 2, 'D': 5},
        'C': {'A': 4, 'B': 2, 'D': 1},
        'D': {'B': 5, 'C': 1}
    }

    # 프림 알고리즘 실행
    result = prim(graph, 'A')
    print(result)  # ([('A', 0), ('B', 1), ('C', 2)], 3)

플로이드

모든 정점 쌍 사이의 최단 거리를 구하는 알고리즘이다. 플로이드 알고리즘의 실행 방법을 살펴보자

플로이드 알고리즘 과정

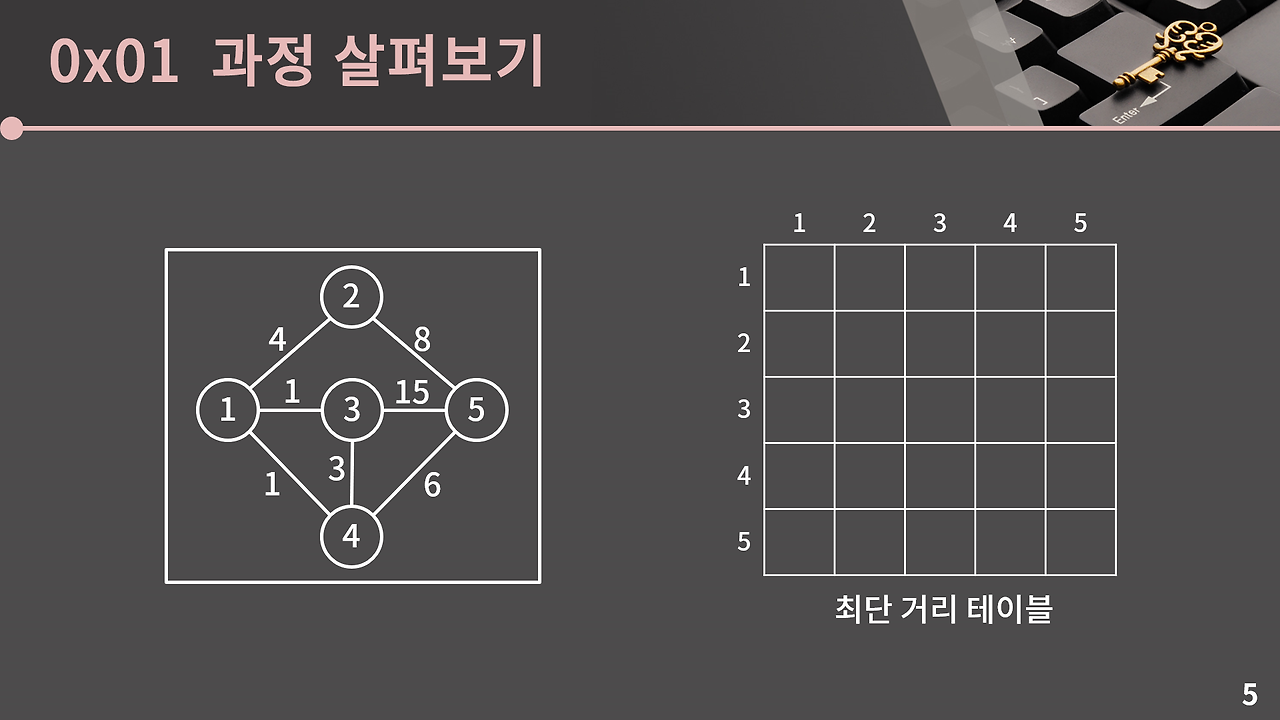
그래프와 빈 테이블이 있다.

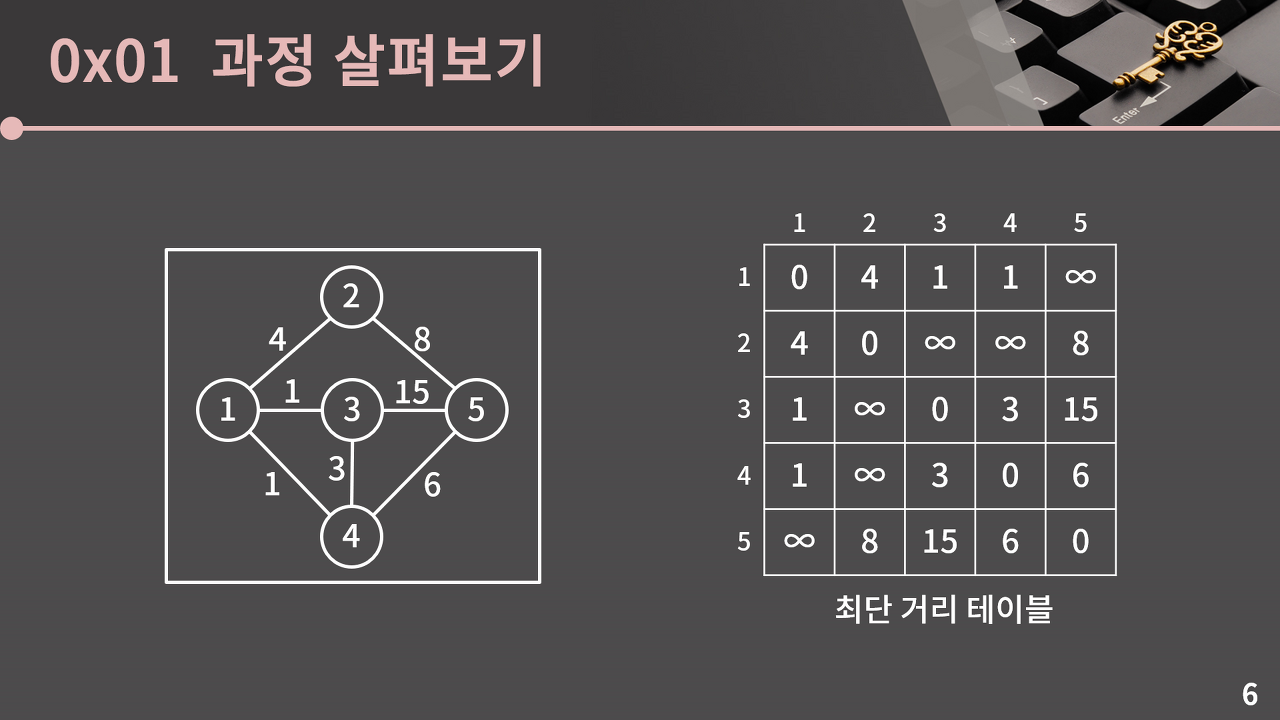
우선적으로 다른 정점을 거치지 않고 연결되어 있는 간선들 중 한번의 단계로 갈 수 있는 간선의 가중치를 테이블에 남겨보면 (3, 5)의 경우 15가 담기고 거리를 알아내지 못한 곳들은 ∞로 채워 놓을 수 있다.

현재 2에서 4로 가는 거리가 ∞인데, 2에서 1을 거쳐 4로 간다면 5의 거리로 갈 수 있기 때문에 수정을 할 수 있다.

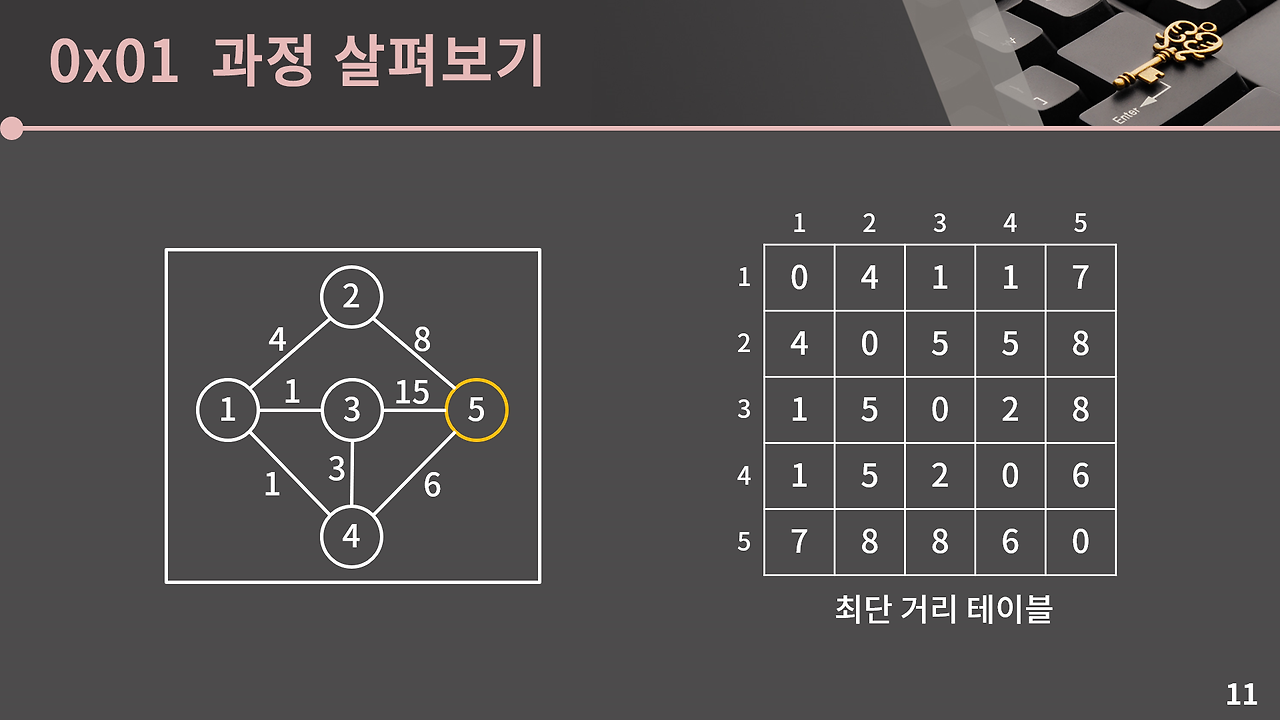
해당 테이블을 D라고 합시다. s에서 t로 갈 때 1번 정점을 거쳐가는 최단 거리는 D[s][1] + D[1][t]입니다. D[s][1] + D[1][t]가 의미하는 바는 s에서 1까지 최단 경로로 가고, 그 후 1부터 t까지 다시 최단 경로로 갔을 때의 값이기 때문입니다. 그렇기 때문에 각 s, t에 대해 만약 D[s][t]보다 D[s][1] + D[1][t]가 작을 경우, 즉 1번 정점을 거쳐가는 것이 효율적일 때에만 D[s][t]를 D[s][1] + D[1][t]로 갱신해주면 됩니다. 결과적으로 주어진 테이블에서는 D[2][3], D[2][4], D[3][2], D[3][4], D[4][2], D[4][3]이 갱신된다.

이렇게 각 정점을 거쳐가는 최단 거리를 구해서 테이블을 작성해보면 다음과 같습니다.

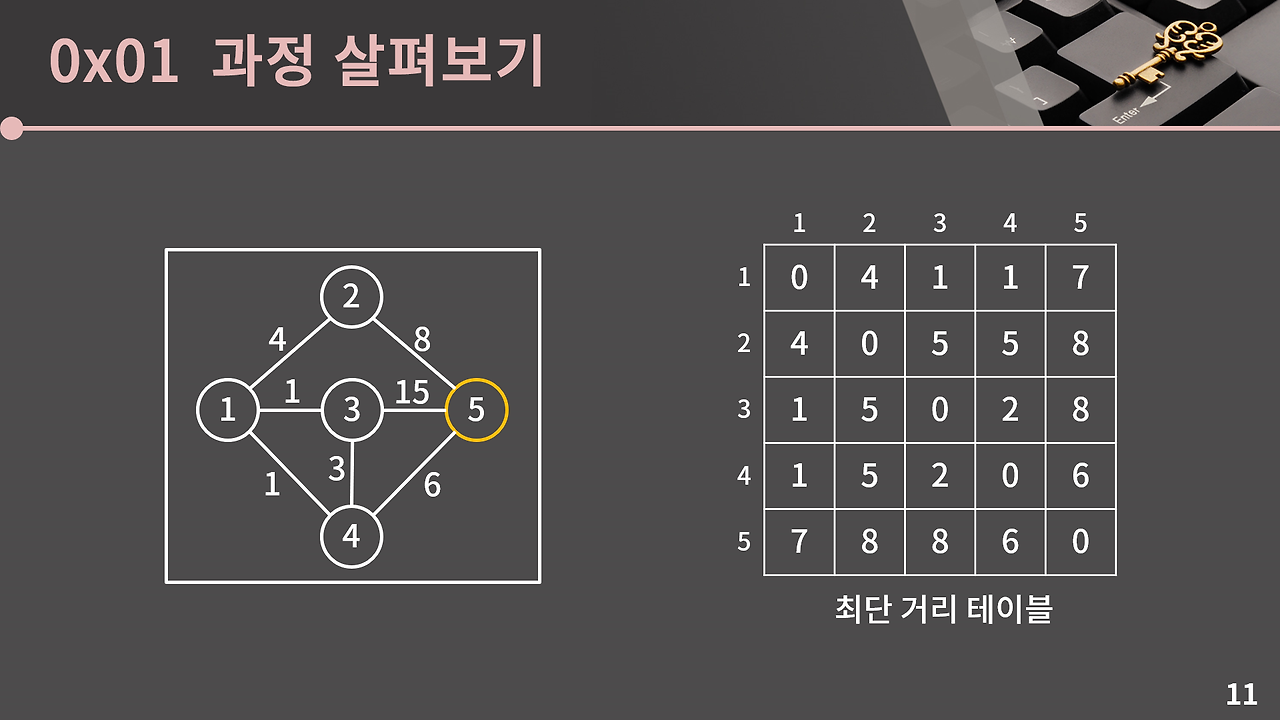
이렇게 플로이드 알고리즘이 종료되었습니다. 정점이 V개라고 할 때 총 V단계에 걸쳐 갱신이 이루어지고 각 k=1,2,3,…,V번째 단계마다 총 V2개의 모든 D[s][t]값을 D[s][k]+D[k][t]값과 비교하므로 플로이드 알고리즘의 시간복잡도는 O(V3)입니다.

플로이드 구현

boj11404에 따른 플로이드 문제의 파이썬 구현 코드입니다.

import sys

city = int(input())
bus = int(input())
graph = [[float("inf")] * (city + 1) for _ in range(city + 1)]

for _ in range(bus):
    s, e, cost = map(int, sys.stdin.readline().split())
    graph[s][e] = cost if graph[s][e] == 0 else min(graph[s][e], cost)

for i in range(1, city + 1):
    graph[i][i] = 0
    for j in range(1, city + 1):
        for k in range(1, city + 1):
            graph[j][k] = min(graph[j][i] + graph[i][k], graph[j][k])

for i in range(1, city + 1):
    for j in range(1, city + 1):
        if graph[i][j] == float("inf"):
            graph[i][j] = 0
        print(graph[i][j], end=' ')
    print()