BOJ 10254 | 고속도로

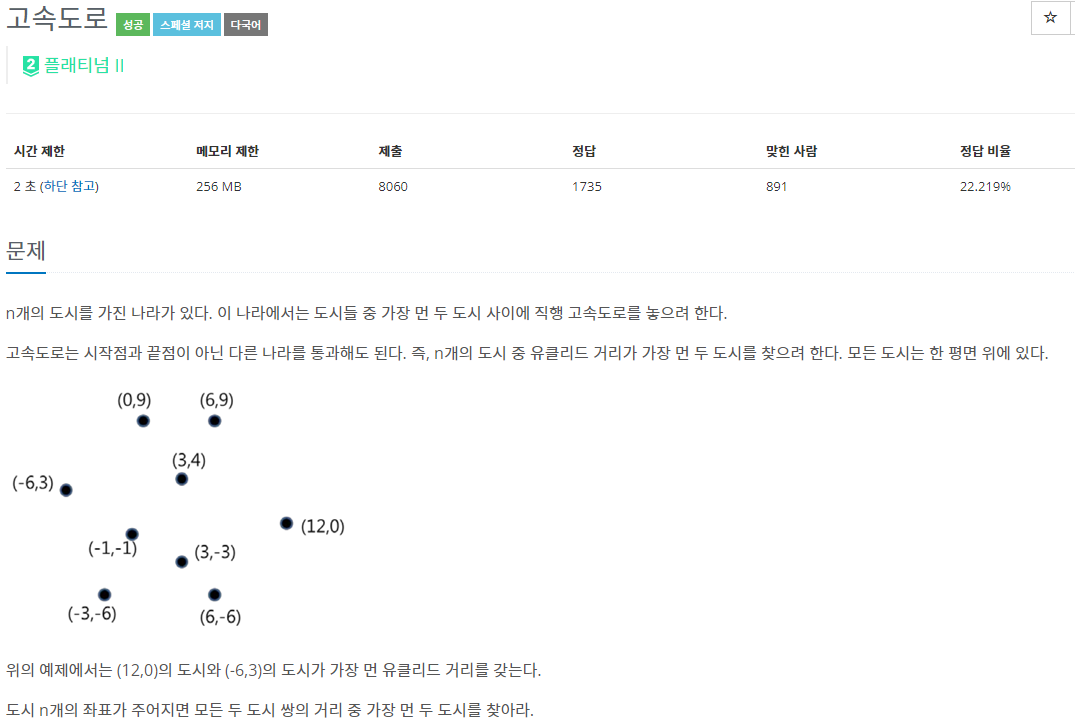
요구하는 조건은 아주 간단하지만 구현이 생각보다 어려운 문제다.

2차원 평면 위에 놓여진 도시들 중 가장 먼 도시를 찾아라. 즉 N개의 점을 전부 비교해서 $O(N^2)$에 해결하는 솔루션이 제일 먼저 떠오른다.

그러나 도시의 개수가 최대 200,000이므로 절대 $O(N^2)$는 해결할 수 없다. 특별한 방법이 필요하다.

이러한 검은 점들이 주어진 도시라고 해보자.
이 중에서 걸러낼 수 있는 도시들은 몇 개가 있을까?

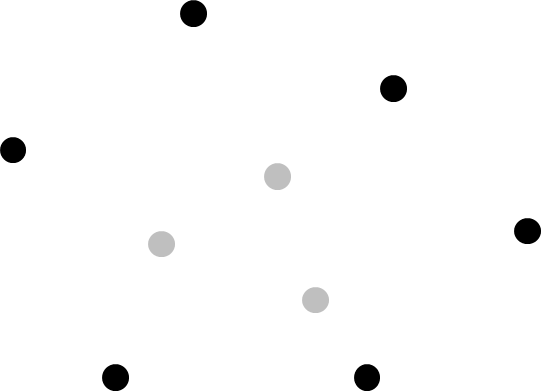
바로 안쪽의 회색 점들이다. 어떤 점에서 연결하더라도 이 점보다 먼 점을 찾을 수 있다.

결국 볼록 껍질을 구성하는 점들만 따져보면 된다.

볼록 껍질을 구하는 알고리즘은 $O(NlogN)$에 가능하므로 그 이후를 생각해보자.

모든 점이 볼록 껍질을 구성하는 점으로 주어지면 가장 먼 도시를 찾는 과정을 $O(N^2)$으로는 해결할 수 없을 것이다.

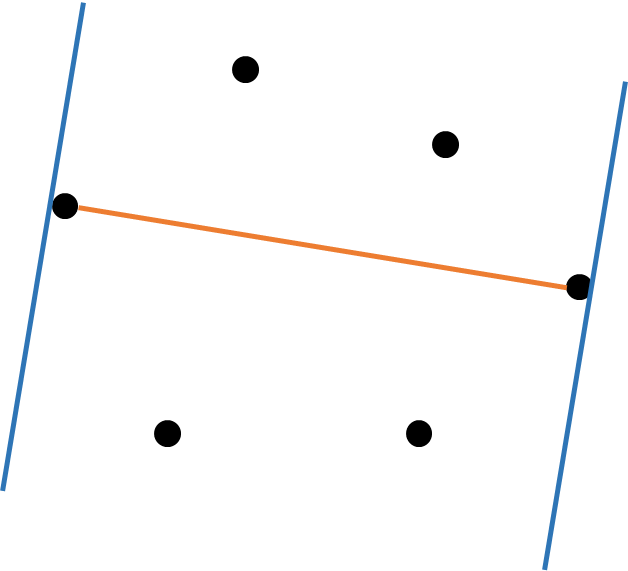
다음과 같이 어떤 점을 잡고, 그 점에 대해 가장 먼 점의 거리를 주황색 선으로 나타냈다. 파란색 선은 주황 선에 대해 수직이다.

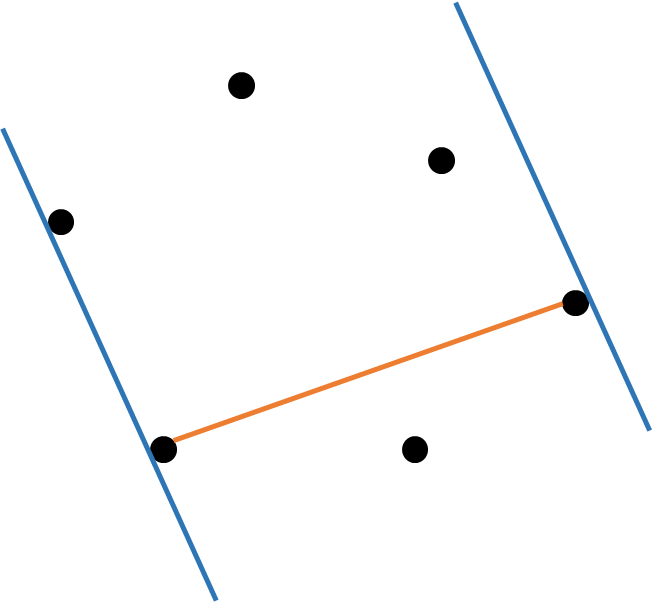
이후 저 파란 선들을 회전시키면서 다음 점에 닿을 때 대상 점을 옮겨서 거리를 잰다.

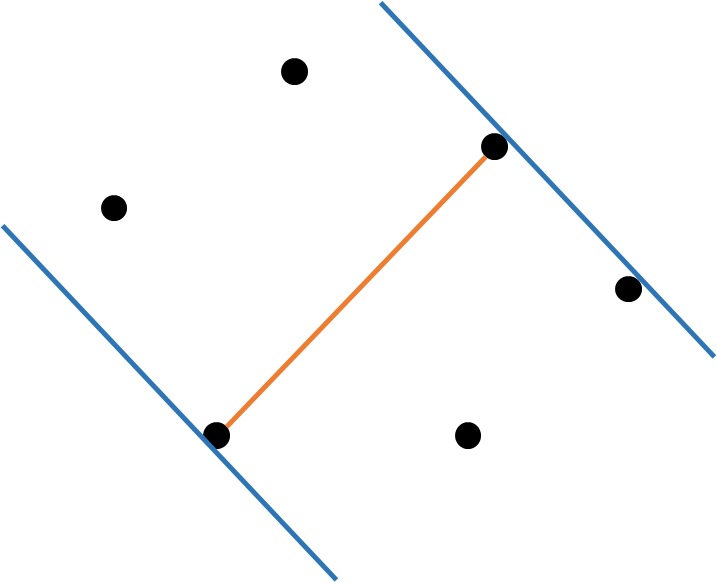
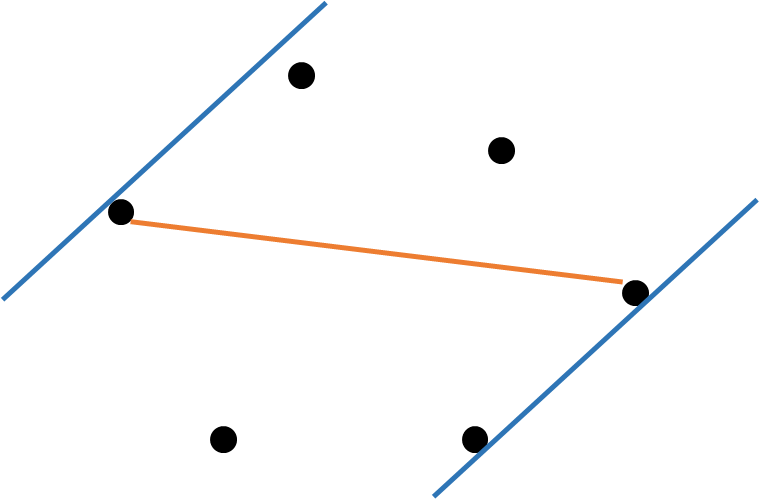
이렇게 다시 원래 점으로 돌아올 때까지 수행하면 $O(N)$에 가장 먼 거리를 구할 수 있다.

그렇다면 이걸 어떻게 코드로 구현할까?
이론은 알았지만 막상 코드로 구현하자니 저 파란 캘리퍼스를 어떻게 구현할지 아이디어가 떠오르지 않을 것이다.

여기서도 CCW가 사용된다.

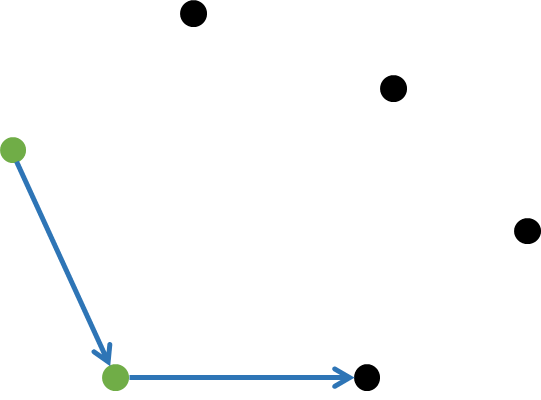
먼저 시작점을 2개 잡는다.
시작점은 어디로 잡든 상관없으니 보통 dot[0]으로 시작한다.
나머지 하나의 시작점은 반시계방향의 점으로 잡는다.

dot[0]은 첫 번째 파란 선의 점이고, dot[1]은 두 번째 파란 선의 점이다.

이제 저 두 선에 대해 CCW를 써보자.

만약 구하려고 하는 두 선이 떨어져 있더라도 $(a, b)$와 $(c,d)$ 의 두 벡터를 $(a, b)$와 $(b, d-(c-b))$로 옮겨주면 구할 수 있다.

CCW가 양수면, 두 선이 반시계방향으로 위치하고 있기 때문에 아직 두 번째 선이 준비되지 않은 것이다. 두 번째 선을 다음으로 옮기자.

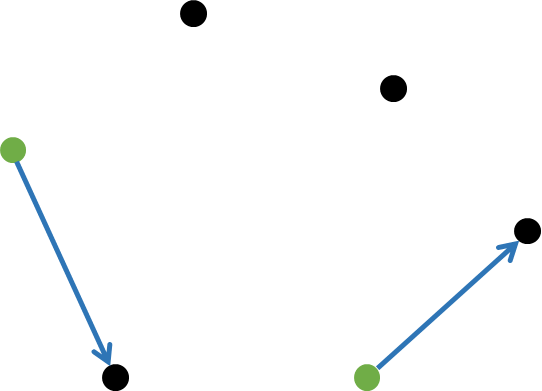
여전히 CCW가 양수다. 다시 한번 옮기자.

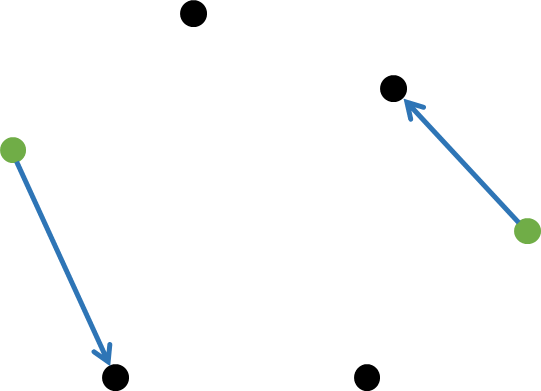
이제 CCW가 음수가 되었다. 두 선분을 이렇게 옮겨서

보면 확실하게 시계방향으로 꺾여있는 것을 볼 수 있다.
정확히 이 시점에 초록 점 2개가 캘리퍼스의 대상 점이 된다.

위에서 설명한 회전하는 캘리퍼스는 항상 두 선이 평행했다. 그러므로 두 파란 선이 평행해야 거리를 잴 수 있는 것이다.

그러니까 여기서도 처음에 파란 선의 CCW가 반시계방향이었으니 초록 점을 한 칸씩 옮겨가며 돌리다 보면, 어느 순간에 반시계 => 평행 => 시계 로 CCW가 변할 것이다. 그 평행한 시점에 거리를 재면 된다.

그런데 우리가 정확히 캘리퍼스가 평행한 시점을 알 수는 없다. 우리는 초록 점을 한 칸씩 옮기고 있기 때문에 CCW는 연속적으로 변하지 않고 파란 선이 두 점과 만나는 시점만을 보여준다.

그래서 이 파란 선이 처음으로 시계방향을 이룰 때, 반시계 => 시계로 변한 것이므로 그 중간 어느 시점에 평행했음을 짐작할 수 있다.

잘 모르겠다면 긴 자를 가져다가 두 파란 선에 놓고 하나를 돌려가면서 움직여보자.

회색 선에서 파란 선으로 움직이는 어느 순간에 평행을 이룰 것이다.

그렇기 때문에 처음 시계방향이 된 두 파란 선의 대상 점의 거리를 잴 수 있다.

이제 거리를 재는 작업 1개를 완료했으므로 첫 번째 파란 선을 한 칸 옮긴다.

이제 다시 CCW가 반시계 방향이 되었으므로 위 작업을 반복하면 회전하는 캘리퍼스를 구현할 수 있다!

코드

#include <bits/stdc++.h>
using namespace std;

#ifdef LOCAL
constexpr bool local = true;
#else
constexpr bool local = false;
#endif

#define ll long long
#define FASTIO ios_base::sync_with_stdio;cin.tie(nullptr);cout.tie(nullptr);

#define debug if constexpr (local) std::cout
#define endl '\n'

ll fx, fy;
vector<pair<ll, ll>> dot;
vector<pair<ll, ll>> edges;

bool cmp(pair<ll, ll> a, pair<ll, ll> b){
	if (a.second != b.second) return a.second < b.second;
	return a.first < b.first;
}

bool _cmp(pair<ll, ll> a, pair<ll, ll> b){
	ll l = (b.first - fx) * (a.second - fy);
	ll r = (a.first - fx) * (b.second - fy);
	if (l != r) return l < r;
	
	if (a.second != b.second) return a.second < b.second;
	return a.first < b.first;
}

ll ccw(pair<ll, ll> a, pair<ll, ll> b, pair<ll, ll> c){
	return (b.first-a.first)*(c.second-b.second)-(c.first-b.first)*(b.second-a.second);
}

void solve(){
	int N; cin >> N;
	dot.clear();
	for (int i = 0; i < N; i++){
		ll x, y; cin >> x >> y;
		dot.push_back({x, y});
	}
	stable_sort(dot.begin(), dot.end(), cmp);
	fx = dot[0].first; fy = dot[0].second;
	
	stable_sort(dot.begin()+1, dot.end(), _cmp);
	
	//for (auto &i : dot) debug << i.first << ' ' << i.second << endl;
	stack<int> task;
	task.push(0);
	task.push(1);
	
	
	int next = 2;
	while (next < N){
		while (task.size() >= 2){
			ll A, B;
			B = task.top(); task.pop();
			A = task.top();
			
			// if ccw(A, B, next) > 0 => B is edge
			if (ccw(dot[A], dot[B], dot[next]) > 0){
				task.push(B);
				break;
			}
		}
		task.push(next);
		next++;
	}
	
	//cout << task.size() << endl;
	
	edges.clear();
	while (!task.empty()){
		int t = task.top(); task.pop();
		edges.push_back({dot[t].first, dot[t].second});
	}
	reverse(edges.begin(), edges.end());
	
	
	//rotating callippus
	pair<ll, ll> a, b, c, d;
	
	/*ll mnx = edges[0].first, mxx = edges[0].first;
	ll mni = 0, mxi = 0;
	for (int i = 0; i < edges.size(); i++){
		if (mnx >= edges[i].first){
			mnx = edges[i].first;
			mni = i;
		}
		if (mxx <= edges[i].first){
			mxx = edges[i].first;
			mxi = i;
		}
	}*/
	
	int pa=0, pb=1, pc=1, pd=2;
	a = edges[pa]; b = edges[pb]; c = edges[pc]; d = edges[pd];
	int flag = 0;
	double mxv = 0;
	pair<ll, ll> d1, d2;
	while (!flag){
		double dist = sqrt((c.first - a.first)*(c.first - a.first) + (c.second - a.second)*(c.second - a.second));
		//debug << "DBG " << dist << endl;
		if (mxv <= dist){
			mxv = dist;
			d1 = a; d2 = c;
			//debug << "UPDATE " << dist << endl;
			//debug << d1.first << ' ' << d1.second << ' ' << d2.first << ' ' << d2.second << endl;
		}
		
		if (ccw(a, b, {d.first-(c.first-b.first), d.second-(c.second-b.second)}) > 0){
			pc = (pc+1) % edges.size();
			pd = (pd+1) % edges.size();
		}
		else {
			pa = (pa+1) % edges.size();
			pb = (pb+1) % edges.size();
			if (pa == 0) flag++;
		}
		a = edges[pa]; b = edges[pb]; c = edges[pc]; d = edges[pd];
	}
	
	cout << d1.first << ' ' << d1.second << ' ' << d2.first << ' ' << d2.second << endl;
	
}

int main(){
	FASTIO;
	int T; cin >> T;
	for (int i = 0; i < T; i++){
		solve();
	}
}