BOJ 18440 | LCS 7

LCS 6을 풀었다면 LCS 5와 조합해서 풀 수 있다.
나는 이걸 LCS 6을 풀고도 시간 초과때문에 한참을 더 풀었지만 기본적인 아이디어는 LCS 6과 같으므로 LCS 6은 생략한다.

우선 LCS는 최장 공통 부분 수열이다. 보통은 $O(NM)$으로 구할 수 있지만 이 문제는 $N, M$이 최대 50,000이므로 그렇게 풀 수는 없다.

그렇다고 LCS를 일반적인 상황에서 $O(NM)$ 미만으로 구하기도 어렵다. 대체 어떤 테크닉이 필요한걸까.

• 이 글은 https://koosaga.com/245 을 참고하여 작성되었습니다. (구사과 그는 신이야)

Bitset을 이용한 $O(NM/64)$ 로 LCS를 해결하는 방법에 대해 알아보자.

문자열 $S, T$를 입력받고, 그 LCS를 구해야 한다.

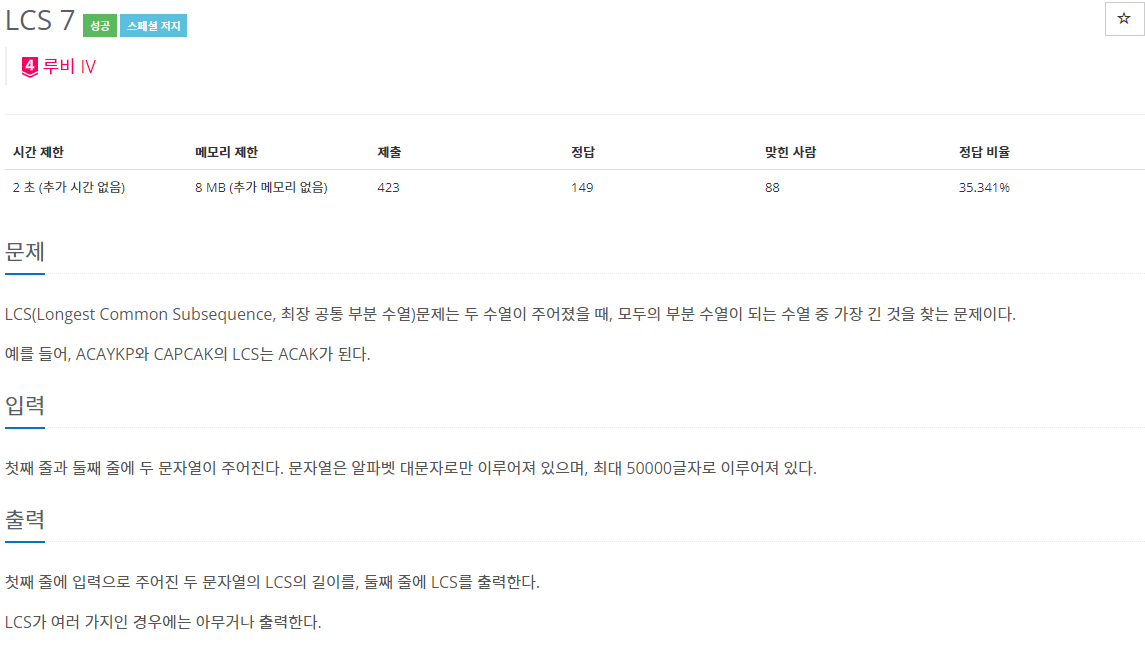
LCS를 구하기 위한 표를 살펴보자.

LCS 5에서 소개했지만 LCS는 토글링을 통해 공간복잡도 O(M)으로 해결할 수 있다. 위 표는 이해를 돕기 위해 전부 그린 것이다.

저 표를 $DP$라고 하고, $i$번째 줄의 $j$번째 칸이 $DP[i][j]$이다.
이 때, $DP[i][j]$는 다음과 같은 점화식으로 나타낼 수 있다.

$DP[i][j] = \begin{cases} 0\ (i == 0\ or \ j == 0)\\ DP[i-1][j-1] +1\;(S[i] == T[j])\\ max(DP[i][j-1],\ DP[i-1][j])\ (S[i]\ != T[j]) \end{cases}$

따라서 다음과 같은 부등식 두 개가 성립한다.
$0\leq DP[i][j] - DP[i][j-1] \leq 1$,
$0\leq DP[i][j] - DP[i-1][j] \leq 1$

$DP[i][j] - DP[i][j-1]$ 값은 0과 1로만 표현되므로 bitset으로 나타낼 수 있다.
이제 bitset으로 나타낼 수 있게 $DP$를 변형해보자.

$B[i][j] = DP[i][j] - DP[i][j-1]$로 두면, $B[i]$는 bitset이다.

이제 $DP$가 아닌 $B$로 그려진 표를 보자.

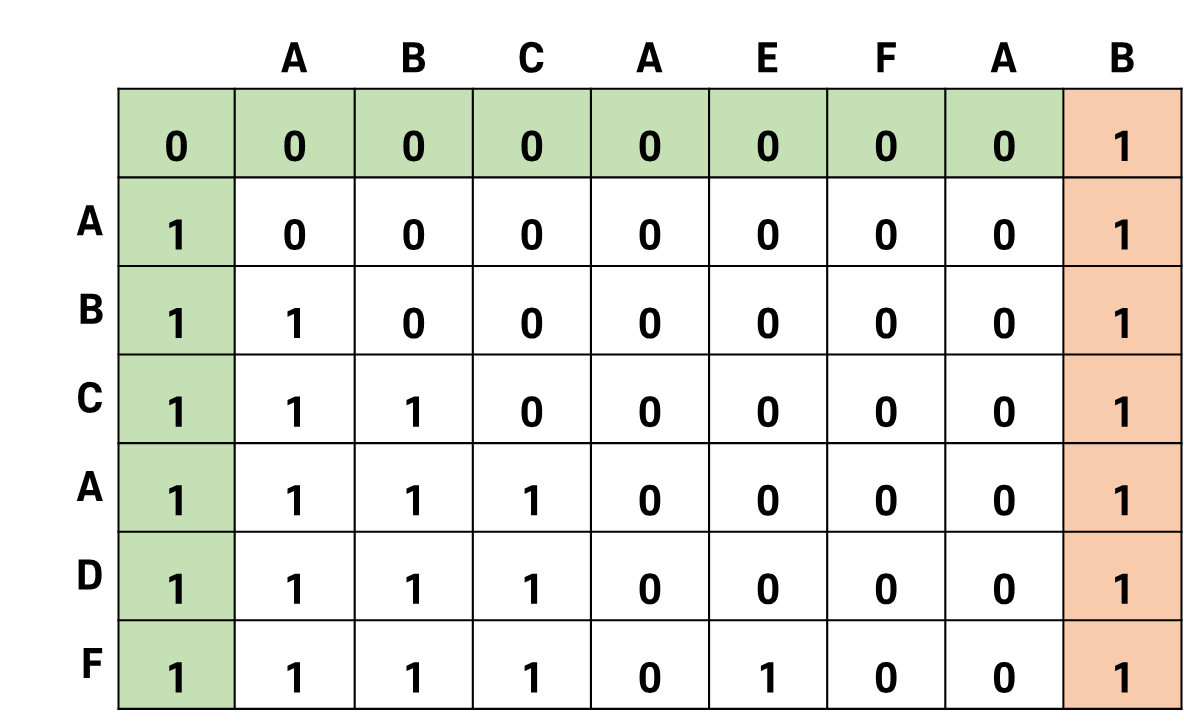
저 오른쪽의 빨간색 칸들의 $B[i][j]$ 값은 정의상 구할 수 없으므로 임의로 전부 1로 설정했다고 하자.

만약 $B[i]$를 이용해서 $B[i+1]$을 구할 수만 있다면 이제 아무 문제 없이 LCS를 구할 수 있다!

비트 연산을 이용하기 위해 $Match[k][x]$ 를 정의하자.
$Match[k][x] = (T[x+1] == k)$이고, $k$는 알파벳이므로 $0 \leq k \leq 25$이다.
값이 true와 false로 나타내지기 때문에 $Match[k]$는 bitset으로 쓸 수 있다.

$B[i+1]$을 구하는 과정에서, $Match[S[i+1]]$을 사용하면 조건문 없이도 $S[i+1] == T[j+1]$인 $j$를 구할 수 있다.

위 그림은 $i=3$일 때 $Match[S[i+1]]$을 나타낸 것이다.
파란색으로 칠해진 부분은 1, 칠해지지 않은 부분은 0이다.
이 때 가지고 있는 정보로는 $B[i] = 100000111$, $Match[S[i+1]] = 001001001$ 이 있다.

이제 이걸 활용해서 $B[i+1]$를 구하는 연습을 해보자.
우선 범위를 잡아보자.

$Match[S[i+1]][j] = 1$이라고 해서 무조건 $B[i+1][j]$가 $1$이 되는 것은 아니다.
파란색 $(A,\ F)$ 칸을 보면 알겠지만 그 다음 칸에서 $S$와 $T$ 모두 $[A]$로 같아도 이미 구간 내에서 1회 증가했기 때문에 증가가 반영되지 않았다.
$AAAAA$와 $AA$의 LCS도 $AAAAAAA$와 $AA$의 LCS도 모두 $AA$로 같다는 점을 생각해보면 이해가 쉬울 것이다.

여기서 구간은 $B[i][j_n] = 1$인 모든 $j_0, j_1, ..., j_m$에 대해 $[j_{x-1}+1, j_x]$를 의미한다.
0에서는 예외로 $[0,\ j_0]$이고, 나머지는 $[j_0 + 1, j_1]$, $[j_1 + 1, j_2]$, ... 로 진행하는 각각의 구간 안에는 무조건 1이 존재한다.

$B[i]$에서 각각의 구간에는 정확히 $1$이 1개 존재하고, 나머지는 $0$으로 채워진다.

구간을 나눠서 표시한 그림을 보자.

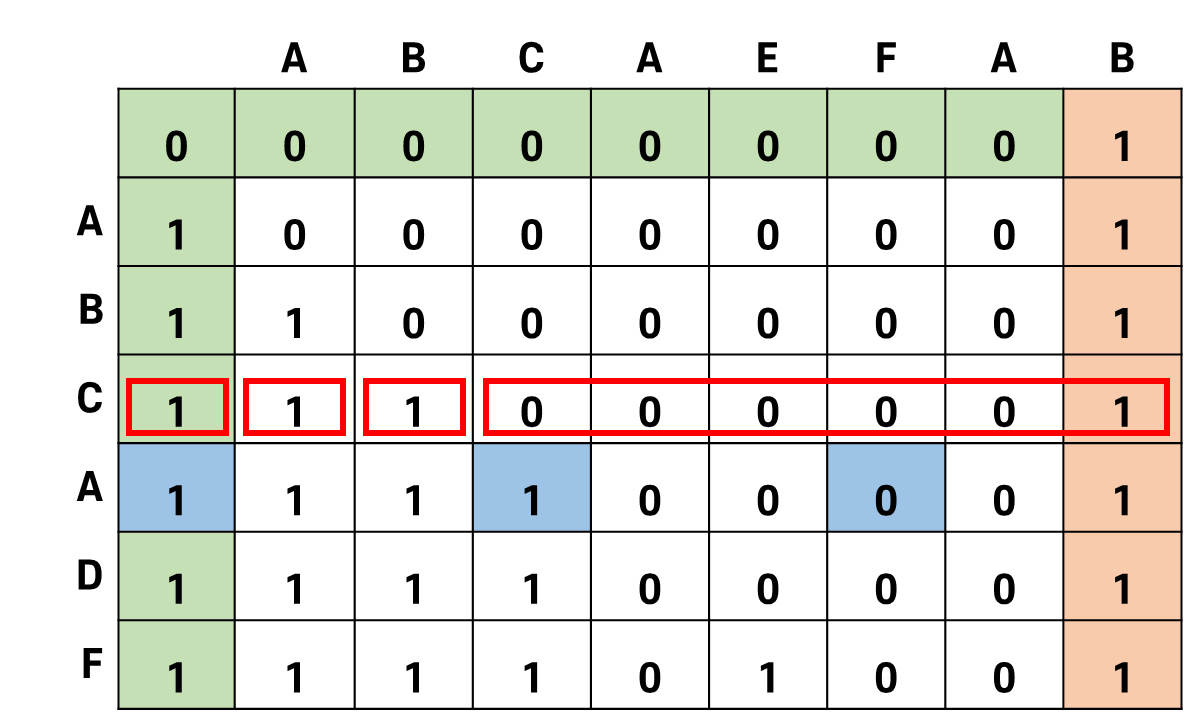
$Match[S[i+1]]$을 반영해줄 때, 이 구간 내에서 $B[i][j] = 1$인 $j$는 단 하나여야 하기 때문에 구간 내부에서 가장 작은 비트로 $B[i][j_x]$를 옮겨주면 된다.

이것을 구현하기 위해서 먼저 $X = Match[S[i+1]]$ | $B[i]$ 를 만들어서 살펴보자.

같은 색깔이 하나의 구간이다.
각 구간마다 $1$은 하나여야 하는데, 파랑 구간에서는 3개의 $1$이 발견되었다.
LCS 배열은 왼쪽부터 작성되기 때문에 각 구간마다 가장 왼쪽의 $1$을 남겨야 한다.

그러므로 각 구간마다 가장 낮은 비트만 살려주면 되는데, 어떤 정수 x에서 가장 낮은 비트에 있는 1만을 남길 때는 x ^ (x & (x-1))로 할 수 있다.
그러므로 각 구간 x에 대해 (x-1)을 해줘야 한다.
$X = 101001\ 1\ 1\ 1$이고, 각 구간마다 1이 들어가 있는 bitset $S = 000001\ 1\ 1\ 1$만 있다면 $X-S$로 각 구간에 대해 (x-1)을 해 줄 수 있다.

그런데 $B[i]$의 각 구간이 $1$로 시작한다는 걸 생각하면 $S = (B[i] << 1)$ | $1$ 이다.
( 10000 1000 100 1000 10000 .... 10 같은 $B[i]$가 있다고 가정하면 $(B[i] << 1)$ | $1$은 00001 0001 001 0001 00001 ... 01 이 된다. )

따라서 $B[i+1]$을 이제 구할 수 있다.
$X = Match[S[i+1]]$ | $B[i]$
$Y = (B[i] << 1)$ | $1$
일 때,
$B[i+1] = X$ ^ $(X$ & $(X - Y))$

드디어 비트 연산과 bitset만을 사용해서 $B[i]$로 $B[i+1]$을 구할 수 있음을 알아냈다!

bitset끼리 빼는 연산은 내장되어 있지 않으므로 직접 구현해야 한다.
나는 cgiosy님의 bitset subtraction을 가져와 사용했다.
https://gist.github.com/cgiosy/a441de545c9e96b1d7b02cc7a00561f9?fbclid=IwAR0N3Woe8GwzAsxMapbEE9b7rrE_XArl50BRdQ9ZOTCxk-2X5BRrm-HBVpo

여기까지 구현했다면 LCS 6을 맞을 수 있다.

LCS 7은 bitset<50000>을 사용했더니 LCS를 수행할 때마다 초기화 해 주는 시간이 생각보다 긴지 시간초과가 계속 났다.

bitset은 resize도 지원하지 않아 직접 bitset을 구현하다가 몇 번 구현이 꼬여 멘붕이 왔다.
(새벽시간에 PS하면 한번 뇌정지가 왔을 때 되살아나기가 좀 어렵다.)

그래서 누군가 bitset 구현해놓은걸 찾아보다가 jinhan님의 풀이를 봤다.
https://blog.naver.com/PostView.naver?blogId=jinhan814&logNo=222546054891&parentCategoryNo=52&categoryNo=11&viewDate=&isShowPopularPosts=false&from=postView

솔직히 천재라고 생각했다.
template<std::size_t sz>를 이용해서 LCS 함수를 호출하는 _LCS 함수를 만든 뒤
_LCS 함수에서 적당히 문자열 b의 크기를 검사해서 LCS<200>, LCS<1000>, LCS<2000> 등 적절하게 분류해서 bitset의 크기를 만들어줬다.
bitset이 동적 할당이 안되는걸 저렇게 처리하다니...

저 방법을 채용해서 맞았고, 추후에 bitset을 직접 구현해서도 풀어볼 예정이다.

코드

#define private public
#include <bitset>
#undef private

#include <bits/stdc++.h>
#include <x86intrin.h>
using namespace std;

#ifdef LOCAL
constexpr bool local = true;
#else
constexpr bool local = false;
#endif

#define FASTIO ios_base::sync_with_stdio;cin.tie(nullptr);cout.tie(nullptr);
#define short unsigned short

#define debug if constexpr (local) std::cout
#define endl '\n'

// https://gist.github.com/cgiosy/a441de545c9e96b1d7b02cc7a00561f9?fbclid=IwAR0N3Woe8GwzAsxMapbEE9b7rrE_XArl50BRdQ9ZOTCxk-2X5BRrm-HBVpo
// Bitset Subtraction
template<size_t _Nw> void _M_do_sub(_Base_bitset<_Nw> &A, const _Base_bitset<_Nw> &B) {
	for(int i=0, c=0; i<_Nw; i++)
		c=_subborrow_u64(c, A._M_w[i], B._M_w[i], (unsigned long long*)&A._M_w[i]);
}
template<> void _M_do_sub(_Base_bitset<1> &A, const _Base_bitset<1> &B) {
	A._M_w-=B._M_w;
}
template<size_t _Nb> bitset<_Nb>& operator-=(bitset<_Nb> &A, const bitset<_Nb> &B) {
	_M_do_sub(A, B);
	return A;
}
template<size_t _Nb> inline bitset<_Nb> operator-(const bitset<_Nb> &A, const bitset<_Nb> &B) {
	bitset<_Nb> C(A);
	return C-=B;
}	

string a, b;
string result;

template<size_t sz> 
vector<int> _LCS(string a, string b){
	bitset<sz> Match[26], x, B;
	for (int i = 0; i < b.length(); i++){
		Match[b[i]-65][i] = 1;
	}
	for (int i = 0; i < a.length(); i++){
		x = Match[a[i]-65] | B; B <<= 1; B |= 1;
		B = x ^ (x & (x-B));
	}
	
	//debug << "B[i] " << B << endl;
	vector<int> ans(b.length()+2);
	for (int i = 0; i < b.length(); i++){
		ans[i+1] = ans[i] + B[i];
	}
	return ans;
}

vector<int> LCS(string a, string b){
	if (b.length()+5 < 100) return _LCS<200>(a, b);
	if (b.length()+5 < 500) return _LCS<1000>(a, b);
	if (b.length()+5 < 1000) return _LCS<2000>(a, b);
	if (b.length()+5 < 5000) return _LCS<10000>(a, b);
	if (b.length()+5 < 10000) return _LCS<20000>(a, b);
	return _LCS<50005>(a, b);
}

void solve(int s1, int e1, int s2, int e2){
	if (s1 == e1){
		for (int i = s2; i <= e2; i++){
			if (a[s1] == b[i]){
				result += a[s1];
				break;
			}
		}
		return;
	}
	
	int mid = (s1 + e1) / 2;
	string upside = a.substr(s1, mid-s1+1);
	string downside = a.substr(mid+1, e1-mid);
	
	string brange = b.substr(s2, e2-s2+1);
	
	//debug << upside << ' ' << downside << ' ' << brange << "#\n";
	
	vector<int> upper = LCS(upside, brange);
	
	reverse(downside.begin(), downside.end());
	reverse(brange.begin(), brange.end());
		
	vector<int> lower = LCS(downside, brange);
	reverse(lower.begin(), lower.end());
	
	//for (auto &i: upper) debug << i << ' '; debug << endl;
	//for (auto &i: lower) debug << i << ' '; debug << endl;
	
	int mxv = -1; int idx = 0;
	for (int i = s2-1; i <= e2; i++){
		if (mxv <= upper[i-s2+1] + lower[i-s2+2] ){
			mxv = upper[i-s2+1] + lower[i-s2+2];
			idx = i;
		}
	}
	
	solve(s1, mid, s2, idx);
	solve(mid+1, e1, idx+1, e2);
	
}

int main(){
	FASTIO;
	//ifstream cin("test.in");
	cin >> a >> b;
	
	solve(0, a.length()-1, 0, b.length()-1);
	cout << result.length() << '\n' << result;
}