deep-learning (4)

오늘의 주제

오늘은 '밑바닥부터 시작하는 딥러닝' chapter 5 오차역전파법에 대해서 다뤄보도록 하겠다.

계산 그래프

계산 그래프란 계산 과정을 그래프로 나타낸 것이다. 여기서 그래프는 자료구조 그래프를 의미하며, 여러개의 노드와 에지로 구성된다.

하나의 문제를 계산 그래프로 나타내 보았다.

A학생은 마트에서 사과를 2개, 귤을 3개 샀습니다. 사과는 1개에 100원, 귤은 1개에 150원입니다. 소비세가 10%일 때 지불 금액을 구하세요.

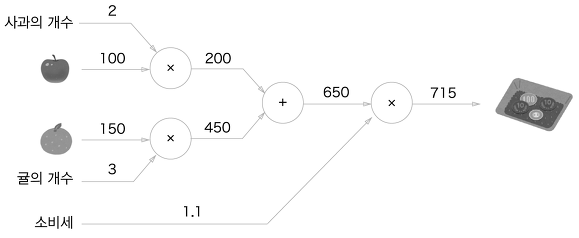
출처 : 밑바닥부터 시작하는 딥러닝

계산 그래프는 왼쪽에서 오른쪽으로 계산을 진행한다. 이렇게 계산을 왼쪽에서 오른쪽으로 진행하는 단계를 순전파 라고 한다. 출발점부터 종착점으로의 전파를 의미하기도 한다. 반대로, 오른쪽에서 왼쪽으로 진행하는 역전파도 존재한다. 이 역전파는 미분 계산에 사용한다.

국소적 계산

계산 그래프의 특징은 국소적 계산을 전파하여 최종 결과를 얻는다는 것이다.

국소적 계산은 전체에서 어떤 일이 벌어지든 상관 없이 자신과 관계된 정보만으로 결과를 출력할 수 있다는 것이다.

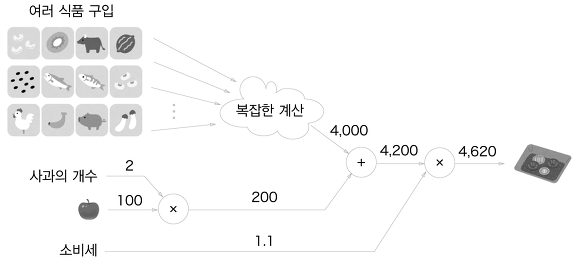
출처 : 밑바닥부터 시작하는 딥러닝

위 그림에서 보면 계산 그래프에서 여러가지 식품을 구입하고, 복잡한 계산 후에 총금액이 4000원이 되었지만, 사과와 다른 값을 더하는 계산은 다른 계산과 상관없이 자신 계산에만 신경쓰면 된다. 그러므로 각 노드는 자신과 관련한 계산 외에는 아무것도 신경 쓸 게 없다.

계산 그래프를 사용하는 이유

계산 그래프는 국소적 계산이라는 특징을 가지고 있어, 각 노드에서 단순한 계산에만 집중하여 문제를 단순화 할 수 있다. 또한 중간 계산 결과를 모두 보관할 수 있다. 이런 장점이 있지만, 진짜 목적은 역전파를 통해 미분을 효율적으로 계산할 수 있다는 것이다.

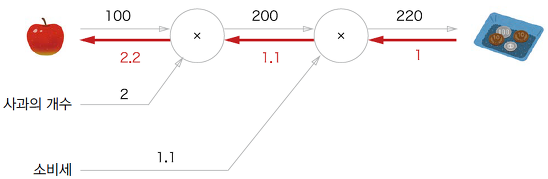
역전파는 반대 방향의 화살표를 이용해 표현한다. 역전파는 국소적 미분 값을 전달하고 화살표 아래에 그 미분 값을 적는다. 역전파를 확인해보면 사과 가격에 대한 지불 금액의 미분값은 2.2인 것을 확인할 수 있다. 여기서는 사과 가격에 대한 미분만 구했지만, 소비세, 사과 개수에 대한 미분 값도 구할 수 있다.

연쇄법칙

위에서 설명한 역전파를 이용한 국소적 미분을 전달 하는 원리는 연쇄법칙을 활용한 것이다.

계산 그래프의 역전파

계산 그래프를 사용한 역전파의 예를 하나 살펴보자.

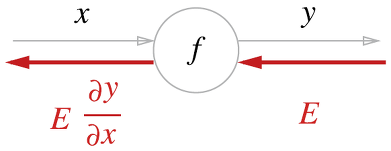
신호 E에 노드의 국소적 미분을 곱한 후, 다음 노드로 전달하는 것이다. 여기서 국소적 미분은 순전파때의 y=f(x) 계산의 미분을 구하는 것이며, x에대한 y의 미분을 구한다는 뜻이다.

연쇄법칙이란?

일단 합성 함수에 대해서 알아보자. 합성 함수란 여러 함수로 구성된 함수이다.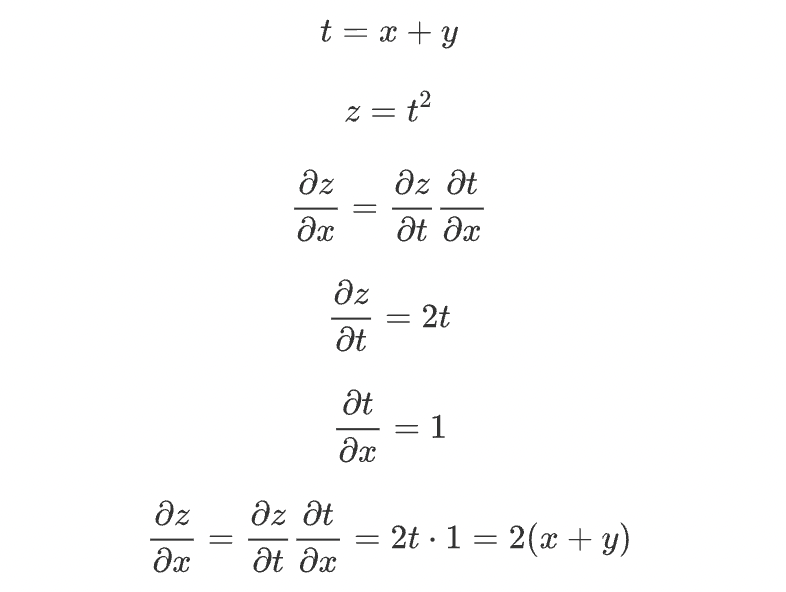

연쇄법칙이란 합성 함수의 미분에 대한 성질이며, 다음과 같이 정의된다.

합성 함수의 미분은 합성 함수를 구성하는 각 함수의 미분의 곱으로 나타낼 수 있다.

위 수식은 합성함수와 연쇄법칙을 이용해서 미분한 식이다.

연쇄법칙과 계산 그래프

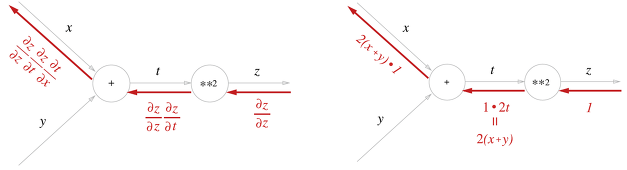
위에서 나타낸 연쇄 법칙 계산을 그래프로 나타낸 그림이다. 오른쪽에서 왼쪽으로 입력 신호에 국소적 미분을 곱하여 다음 노드로 전달하는 모습을 볼 수 있다. 결국 역전파가 끝나면 x에 대한 z의 미분값이 나오게 된다.

역전파

덧셈과 곱하기 등의 연산을 예로 들어 역전파의 구조를 설명하도록 하겠다.

덧셈 노드의 역전파

z = x + y라는 식을 대상으로 그 역전파를 살펴보자.

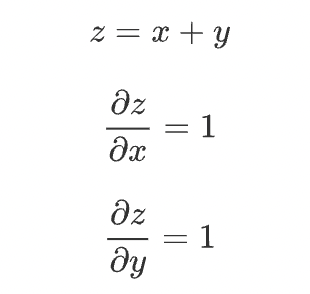
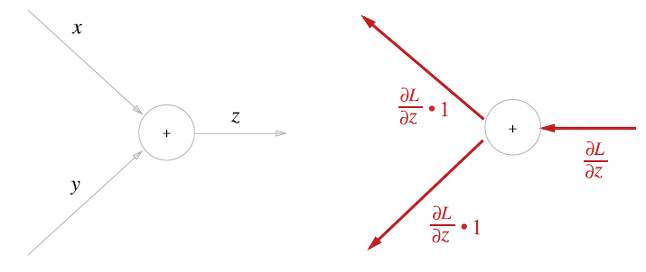
덧셈 노드에서는 상류에서 전해진 미분값에 1을 곱하여 하류로 흘린다. 즉 덧셈 노드의 역전파는 1을 곱하기만 할 뿐이므로 입력된 값을 그대로 다음 노드로 보내게 된다.

곱셈 노드의 역전파

곱셈 노드 역전파를 알아보자. z = xy 라는 식을 예로 들어보자.

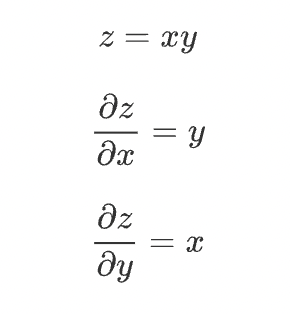
계산 그래프는 다음과 같이 그릴 수 있다.

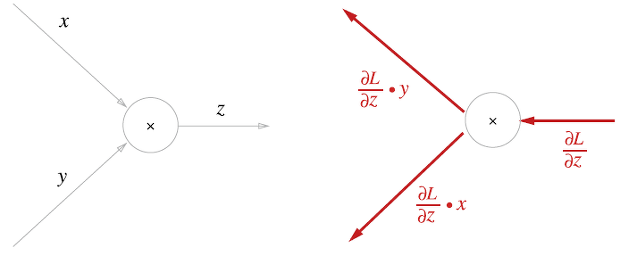
곱셈 노드 역전파는 상류의 값에 순전파 때의 입력 신호들을 서로 바꾼 값을 곱해서 하류로 보낸다. 위 그림처럼 순전파 때 x였다면 역전파에서는 y, 순전파 때 y 였다면 역전파에서는 x로 바꾼다는 의미이다.

단순한 계층 구현하기

곱셈 계층

class MulLayer:    
	def __init__(self):        
    	self.x = None        
        self.y = None            
    def forward(self, x, y):        
    	self.x = x        
        self.y = y        
        out = x * y                
        return out        
     def backward(self, dout):        
     	dx = dout * self.y  # x와 y를 바꾼다.        
        dy = dout * self.x                
        return dx, dy

출처 : 밑바닥부터 시작하는 딥러닝

init 에서는 인스턴스 변수인 x, y를 초기화한다. forward에서는 x와 y를 인수로 받고 두 값을 곱해서 반환한다. backward 상류에서 넘어온 미분에 순전파 때의 값을 서로 바꿔 곱한 후 하류로 흘린다.(역전파)

덧셈 계층

class AddLayer:
	def __init__(self):
    	pass
    def forward(self, x, y):
    	out = x + y
        return out
    def backward(self, dout):
    	dx = dout * 1
        dy = dout * 1
        return dx, dy

덧셈 계층에서는 초기화가 필요 없으니 초기화 함수에서는 아무 일도 하지 않는다. forward에서도 두 인수를 더해서 반환하고, backward에서는 상류에서 내려온 미분 값을 그대로 하류로 흘린다.

활성화 함수 계층 구현하기

신경망을 구성하는 층 각각을 클래스 하나로 구현한다. 일단 활성화 함수 계층을 구현해 보자.

ReLU 계층

활성화 함수로 사용되는 ReLU의 수식은 다음과 같다.

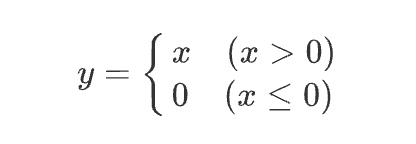
순전파 떄의 입력인 x가 0보다 크면 역전파는 상류의 값을 그대로 하류로 흘린다. 반면 순전파 때 x가 0 이하면 역전파 때는 하류로 신호를 보내지 않는다.

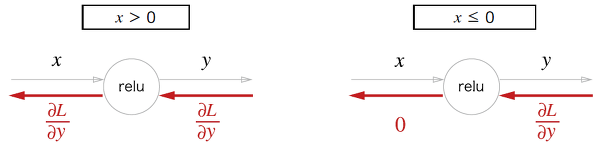
코드는 다음과 같다.

class Relu:
	def __init__(self):
    	self.mask = None
    def forward(self, x):
    	self.mask = (x <= 0)
        out = x.copy()
        out[self.mask] = 0
        
        return out
    def backward(self, dout):
    	dout[self.mask] = 0
        dx = dout
        
        return dx

Relu 클래스는 mask 라는 인스턴스 변수를 가진다. mask는 true/false로 구성된 넘파이 배열로 순전파의 입력인 x의 원소 값이 0 이하인 인덱스는 true, 그 외는 false로 유지한다.

Sigmoid 계층

시그모이드 함수의 식은 다음과 같다.

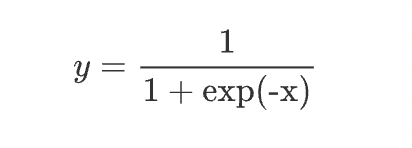
그래프는 다음과 같이 나타낼 수 있다.

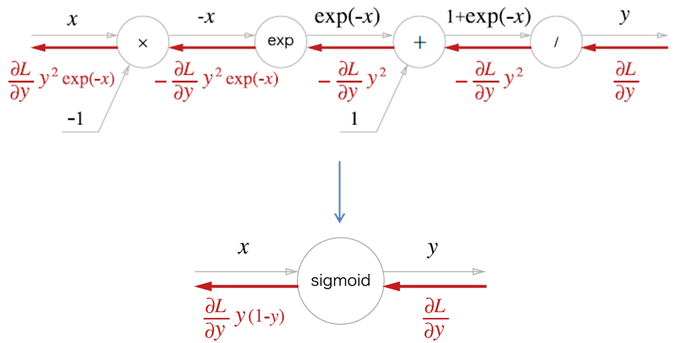
위의 긴 과정을 sigmoid 하나로 묶어서 표현할 수 있다.

여기서 exp 노드는 y=exp(x) 계산을 수행하고 / 노드는 y=1/x 계산을 수행한다.

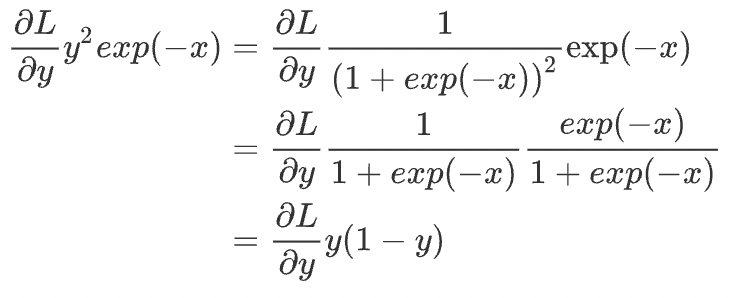
코드는 다음과 같다

class Sigmoid:
	def __init__(self):
    	self.out = None
    def forward(self, x):
    	out = 1 / (1 + np.exp(-x))
        self.out = out
        
        return out
        
    def backward(self, dout):
    	dx = dout * (1.0 - self.out) * self.out
        
        return dx

Affine 계층

우리가 이전 시간에서 배웠던 것에서, 행렬의 곱 계산은 대응하는 차원의 원소 수를 일치시키는 게 핵심이다. 이렇게 신경망의 순전파 때 수행하는 행렬의 곱을 Affine 변환이라고 하며, 이 Affine 변환을 수행하는 처리를 Affine 계층이라는 이름으로 구현한다.

계산 그래프로 나타내면 다음과 같다.

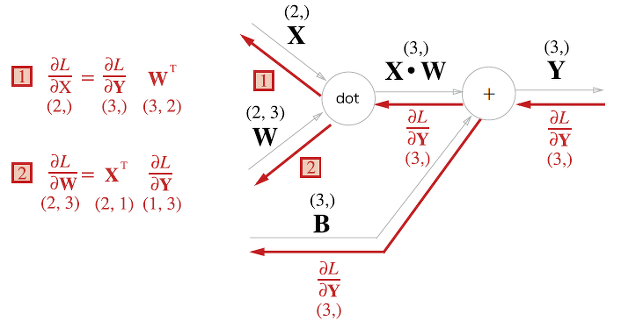
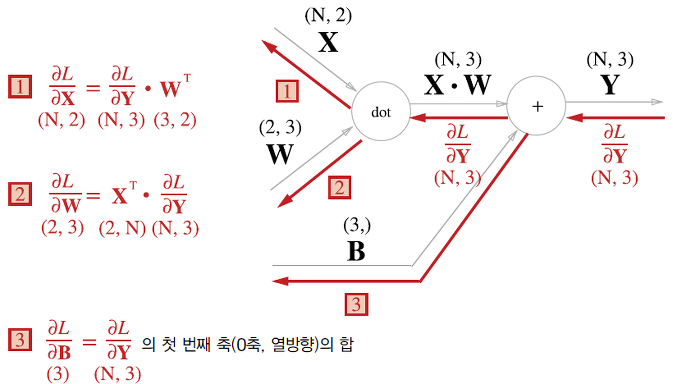
배치용 Affine 계층

위에서 다뤘던 Affine 계층은 입력 데이터로 X 하나만을 고려한 것이다. 이번에는 데이터 N개를 묶어 순전파하는 경우에 사용하는 배치용 Affine 계층에 대해서 알아보자

Softmax-with-Loss 계층

이 전에 다뤘던 것 처럼 소프트맥스 함수는 입력 값을 정규화하여 출력한다.

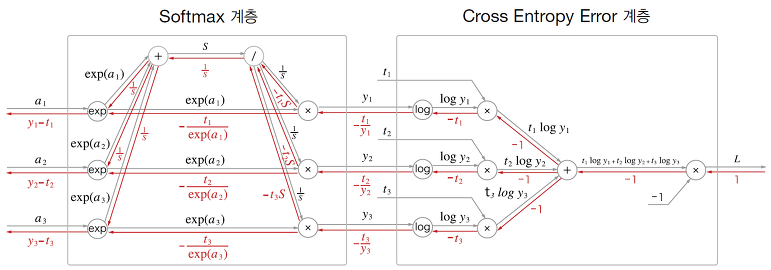
Softmax 계층의 출력과 정답 레이블의 차이를 계산하여, 신경망의 현재 출력과 정답 레이블의 오차를 있는 그대로 드러내는 것이다.

코드는 다음과 같다.

class SoftmaxWithLoss:
	def __init__(self):
    	self.loss = None
        self.y = None
        self.t = None
    def forward(self, x, t):
    	self.t = t
        self.y = softmax(x)
        self.loss = cross_entropy_error(self.y, self.t)
        return self.loss
    def backward(self, dout=1):
    	batch_size = self.t.shape[0]
        dx = (self.y - self.t) / batch_size
        
        return dx

오차역전파법 구현하기

위에 배운 계층들을 조합하면 신경망을 구축할 수 있다.

신경망 학습의 순서

순서는 다음과 같다.

1단계 - 미니배치 : 훈련 데이터 중 일부를 무작위로 가져온다.
2단계 - 기울기 산출 : 미니배치의 손실 함수 값을 줄이기 위해 각 가중치 매개변수의 기울기를 구한다.
3단계 - 매개변수 갱신 : 가중치 매개변수를 기울기 방향으로 아주 조금 갱신한다.
4단계 - 반복 : 위 단계를 반복한다.

마무리

이번 장에서는 계산 그래프, 계산 그래프에서의 순전파와 역전파, 신경망의 구성요소를 계층으로 구현하여 기울기를 효율적으로 계산하는 오차역전파법에 대해서 알아보았다. 다음에는 밑바닥부터 시작하는 딥러닝 chapter 6 학습 관련 기술에 대해서 알아보도록 하겠다.