데이터베이스 인덱스

파일 조직

순차 방법

파일(엔트리순차) 파일
S4 S1 S2 S5 S3 이라면
key(학번) 순차 파일
S1(100) S2(200) S3(300) S4(400) S5(500)
이렇게 ASC로 정렬되어 있다.

정렬이 되어있어야 값을 빨리 찾을 수 있음

인덱스 파일에 키 값대로 정리를 하고 순차 데이터 파일에서는 주소를 넣어 순서대로 정리하는것

역화일

데이터 레코드 파일을 만들어서 K1을 찾으면 그 레코드의 RID를 제공함

다중리스트

키값으로 애트리뷰트 하나에 대해서 테이블을 만들고
하나의 레코드를 저장하고 Pointer를 통해 동일 키 값의 다음 데이터로 이동 할 수 있게 설계함

인덱스 레코드의 값 K1, RID 에 레코드가 여러 개 저장이 된다. K1 {1, 2, 3}

RID리스트가 길수도 짧을수도 있어서 길이가 가변적임

키 순차 파일의 경우 B+트리 사용한다. (클러스터링)

인덱스의 종류

기본 vs 보조 인덱스

• 기본키가 인덱스인가?

집중 비집중

• 데이터 코드가 키 값 순으로 정렬되어 있는가

밀집 희소

• 모든키에 인덱스 엔트리가 있는가

인덱스 엔트리

• <레코드 키 값, 포인터(레코드 주소, RID)>

탐색트리의 종류

2-원 탐색트리

Binary Search Tree
루트가 있고
키값보다 작은게 왼쪽 큰게 오른쪽
inorder를 통해 전부 순회 가능

3-원 탐색트리

기존의 이원탐색트리에서 자식노드를 3개로 늘린 트리이다.
작은값 왼쪽, 사이값 가운데, 큰값 오른쪽 이다,

같은 높이에서도 2-원 탐색보다 더 많은 양의 데이터를 담고 있다.

트리에서의 저장 원리

메모리에 데이터를 저장하는 형태가 될 수 밖에 없음
디스크에 어떻게 저장하는가?

• 페이지 단위로 저장한다 .

하나의 페이지 크기만큼의 노드를 만들고 그 아래에 자식이 여러 개 있는 형태이다. 따라서 1노드는 1페이지.

m-원 탐색 트리

m개의 자식이 있다면 m원 탐색트리이다.

B 트리

M원 탐색트리에서 루트에서 노드까지 깊이가 일정한 것을 균형 탐색트리라고 함

조건

1. 공백이거나 높이가 1이상인 m-원 탐색 트리
2. 루트와 리프를 제외한 내부 노드는 최소 m/2, 최대 m개의 서브트리를 가짐
   (적어도 m/2-1개의 키 값을 가짐)
3. 루트는 그 자체가 리프가 아닌 이상 적어도 두 개의 서브트리를 가짐
4. 모든 리프는 같은 레벨에 있음

디스크 I/O는 H만큼 일어남 (H개의 페이지를 읽기 떄문)
따라서 균형을 유지해야 일정한 시간으로 검색이 가능함

• 어떤 연산을 수행하더라도 균형을 유지해야 함

B 트리 연산

삽입 연산

노드가 오버플로우되면 노드 분할을 시행한다. (split) (m개를 넘으면)
분할을 실행하게되면 상위 노드로 전파됨
최종적으로 루트 노드의 분할로 트리가 깊어짐

삭제 연산

노드가 언더플로우되면 노드 합병(merge) (삭제했더니 n/2보다 작아지면)
합병을 상위 노드로 전파됨
최종적으로 루트의 자식이 병합되면 트리가 얕아짐

삽입 연산

조건 : m개가 저장되어 있을 때

1. m+1 이 되면서 오버플로 발생
2. (m+1) / 2로 분할하고 부모노드에 링크를 추가해서 연결해준다.

예시)
1. 59를 삽입한다 한다.
삽입할 노드에 이미 50 58이 있어서 삽입 후, 50 58 59
3개의 데이터가 된다고 하면 가운데 58을 빼고

실제로는 100개이상의 원소가 있기에 100개에서 가운데 뺴고 반반

반으로 나눠서 작은쪽 반은 원래 노드에 놔두고 나머지 반을 새로 할당된 노드에 놔둔다.
그리고 가운덱 값을 부모노드에 올리게 된다. 이 올라간 가운데 값은 링크의 역할을 한다.

PID 58 RID 59 RID … PID
링크는 이런 형태로 구성되어 있다

2. 54의 경우 들어갈 장소가 없다
   따라서 들어가야하는 노드를 반으로 나누고 가운데값은 부모에 넣는다. (54)

하지만 부모도 삽입을 받았더니 공간이 가득찬다면?
(54 58 60)

1. 똑같이 54 60 으로 나누고 58을 그 부모노드에 넣어서 링크 걸기
2. 또 걸리면 또 분할에서 또 부모노드에 넣기
3. 만약 루트까지 올라와서 부모가 더 이상 없다면 새로운 부모를 만들어서 거기에 넣어야 함

이러한 과정을 통해 루트가 분할하고 트리가 깊어지게 된다.

삭제 연산

60을 지운다고 할 때, 바로 다음 값과 위치를 변경 하고 60을 삭제함 (62)

만약 말단노드에 있는 경우 :
바로 지움 (50 -> 49개가 된다)
n/2보다 작아졌기에 부모와 형제노드를 합한다.
그 후, 삽입때와 마찬가지로 1/2 하고 가운데값을 부모로 두고 나머지를 각각 나눠가진다.

이 과정을 재분배라고 함

B트리의 단점과 B+트리

• 순차접근시 과도한 디스크 IO 발생
• B+트리는 인덱스 세트와 순차 세트로 분리해서 구성함
  • 인덱스 세트는 단순히 리프까지 따라가는 경로만 만드는 것
  • RID는 순차세트 맨 아래 리프노드에만 있음

따라서 B+트리에서는 리프노드까지 가야지 RID를 받아올 수 있음. 중간 인덱스들을 통해서 리프까지 갔더니 리프에는 없을 수도 있다. (근데 이러면 시간 날린거 아닌지?)

밀집인덱스 희소인덱스

모든 데이터 레코드에 대한 링크가 있는 것이 아니라 희소인덱스이다. 순차세트의 인덱스는 모든 데이터에 대한 RID를 가지고 있기 떄문에 밀집인덱스이다.

노드에 대한 것을 더 정확하게 그리면 PID KEY RID KEY RID … PID (이중연결리스트처럼 이전과 이후를 모두 가리킬 수 있게 설계되어있음)

Where 40 <= id <= 90 같은 질의를 빠르게 처리 가능함(말단에서 왔다갔다만 하면 된다)

1) Point Query : select 40
2) Range Query: 40 <= id <= 90

B+트리의 연산

삽입

B트리와 유사
항상 리프노드에서만 삽입 삭제가 일어남

삭제

B트리와 유사
항상 리프노드에서만 삽입 삭제가 일어남

삭제 예시)

• 43을 삭제 (그대로 삭제하면 된다)

• 125 삭제

  • 125를 삭제하고 나면 반 이상 차있지않음
    따라서 재분배 시행
  • 70 90 110 120 을 제분배하면 부모포인터 값을 조정해줘야함
  • 90 ~ 110 사이의 값을 부모의 값으로 설정함
    그 후 값을 분할 7090 ---- 110120

• 55를 삭제

  • 언더플로우 발생, 재분배도 1.5개라서 불가
    이럴떄는 merge해서 35 40 69로 합해지고 링크를 하나 지워줌(링크의 경우 지워도 크게 영향없다)

Sqlite의 경우 key rid가 들어가지 않고
Key datarecord를 넣어둠 > 키 순차파일이 형성된다

해시, 비트맵

해싱 방법

다른 레코드참조 없이 목표 레코드의 접근을 직접 지원한다.
키 값과 레코드 주소 사이의 사상 관계를 함수로 설정

해싱 함수

키 값으로부터 레코드 주소를 계산

버킷 해싱

키 -> 버킷 주소
버킷 하나가 여러 페이지로 구성되어서 여러 레코드가 들어갈 수 있다. 이때, 서로다른 key가 동일한 버킷에 들어 갈 수 있음. 실제로는 10000 / n 개가 평균적으로 버킷에 들어가고 가득차게 될 수 있음.
--> 충돌 발생

충돌 : 상이한 레코드들을 같은 주소(버킷)로 변환

• 동거자
• 버킷 만원 (오버플로)
• 한번의 I/O추가

확장성 해싱

충돌에 대처하기 위해 제안된 기법
레코드 검색은 최대 2번의 디스크 접근

• 모조키
  • 모조키를 통해서 해싱의 충돌을 막는다
• hash prefix
  • 해시값을 읽을 때 몇 비트를 읽을것인가

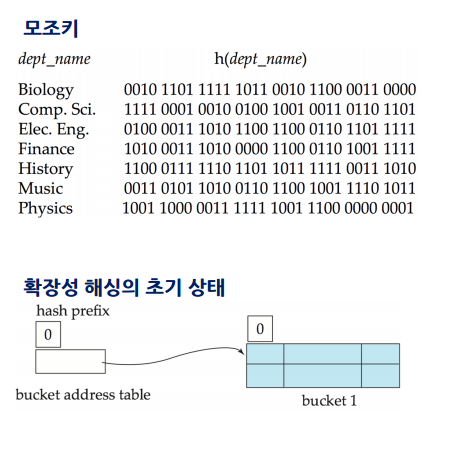
    확장성 해싱에서의 삽입

    초기상태
    prefix = 0
• 버킷에는 Key Rid가 아니라 Key Record 이렇게 레코드 자체가 들어감
• 만약 공간이 없다면 분할을 실행하고 prefix 0비트를 1로 바꿈
• 카테고리별 모조키의 값을 확인하고 모조키 자리수의 값에 따라서 0 혹은 1에 맞춰 저장함
• 하지만 이렇게 나눴지만 또 저장장소가 없다면, 가득 찬 저장버킷을 또 나누고 bit를 하나씩 올림. prefix도 하나 올림.

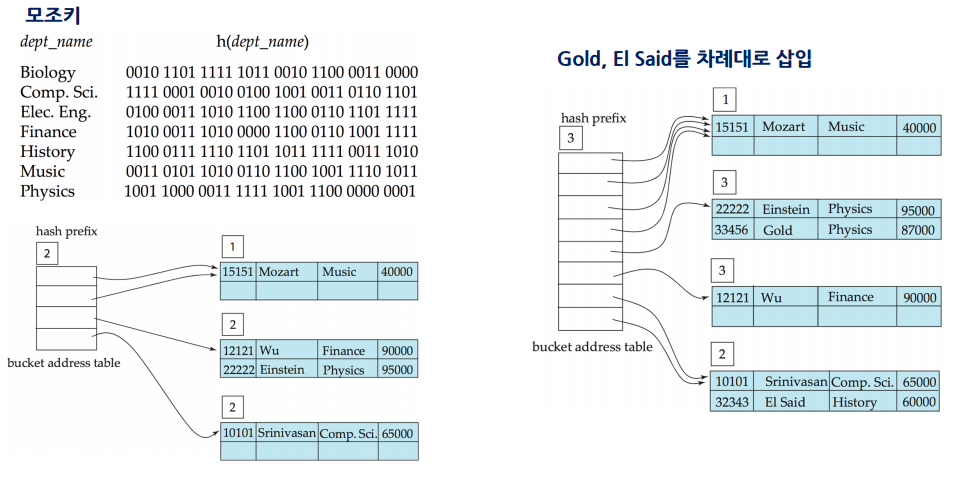
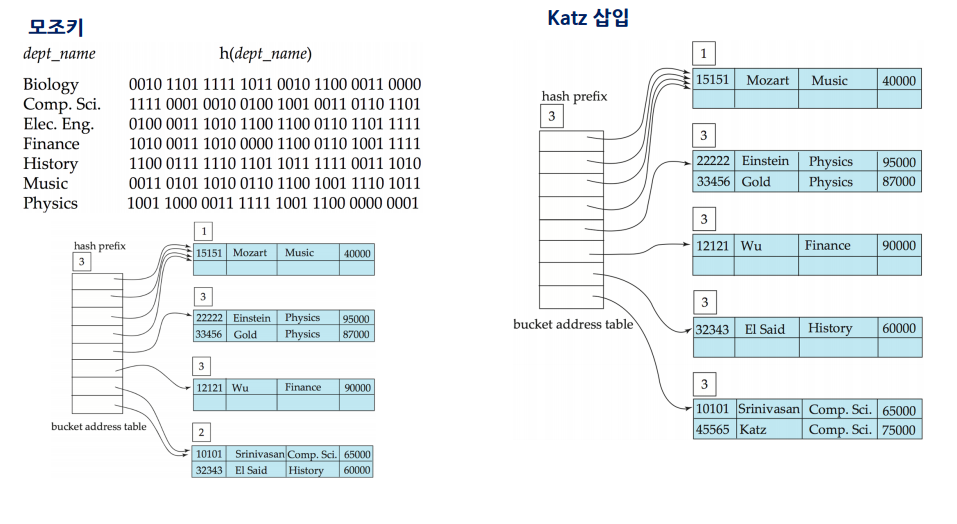
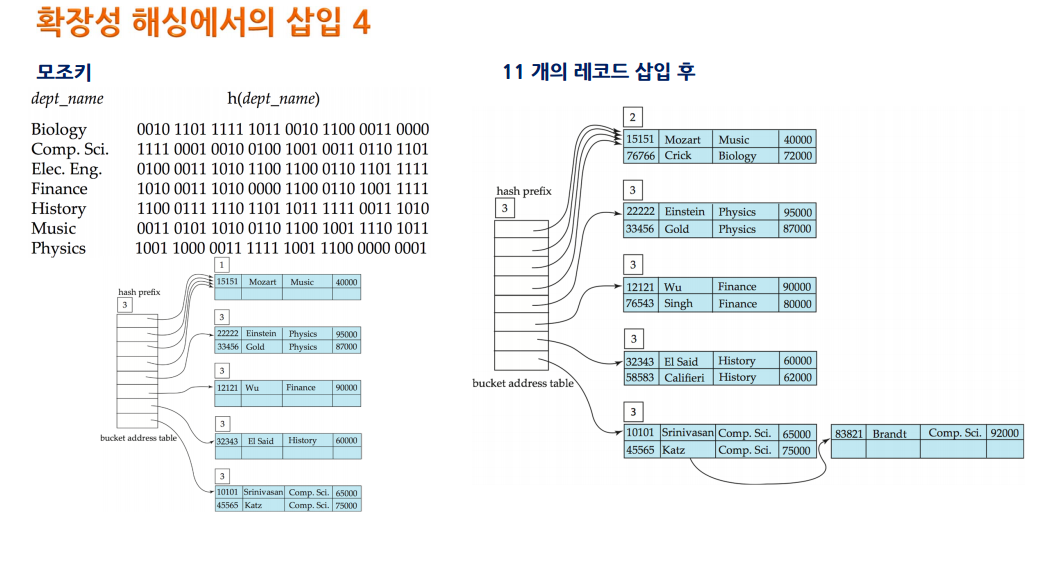
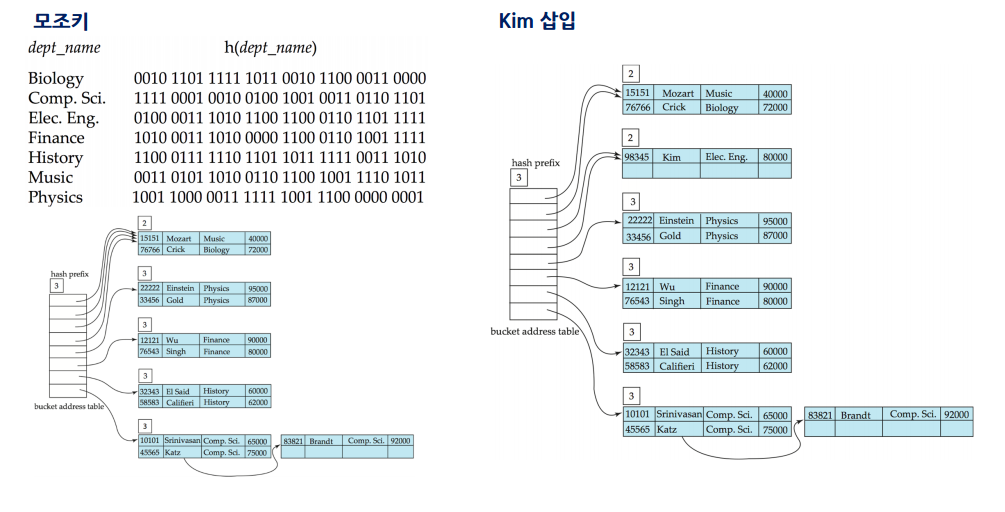
1 50 60 --> 2 50 50 60 60 이런식으로 늘어남 (각 주소는 이진수로 찾음) --> 3 50 50 50 50 60 60 80 70 이런식으로 복사해서 늘어나면서 새로 만든 주소를 하나 끼워넣음 그 후 앞에 prefix 숫자의 비트수만큼 모조키 앞 비트를 보고 맞는 위치에 자료를 넣음.

비트맵 인덱스

애트리뷰트 값이 얼마 안되는 경우
소득수준, 성별, 국가 등

있는 위치 1, 없는 것 0 하고 AND OR NOT 연산 이용해서 풀이한다.
출처

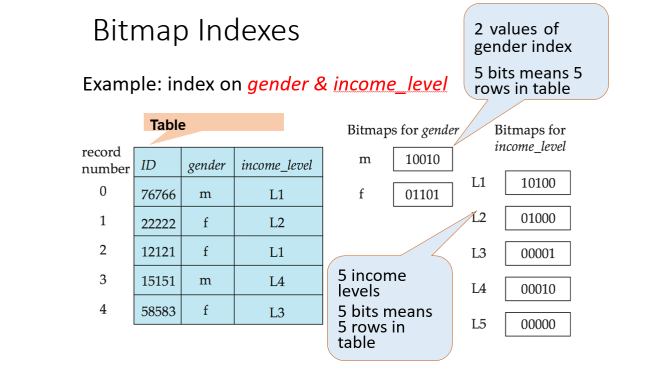
질의 예

• gender = ‘m’ AND income_level = ‘L1’
  • 10010 AND 10100 = 10000
• income_level = ‘L1’ OR income_level = ‘L2’
  • 10100 OR 01000 = 11100
• income_level != ‘L1’
  • NOT 10100 = 01011

비트맵 인덱스에서의 삭제

존재 비트맵

• 유효한 레코드 기록
  • ex) 5개 모두 유효 11111

2번 레코드 삭제 11011 (인덱스 번호 2번임)

질의 실행 시 존재 비트맵과 항상 AND연산 수행

• income level != L1
  • 10100 and 11011 = 10000 삭제

Null 값이 있는 경우 Null 비트맵을 따로 두어서 해결 가능 00001 00000

다중 키 파일 R TREE
GIS 데이터에서 사용함.

인덱스를 만들어야하는 이유
인덱스가 레코드와 같이 있어서 삽입 삭제 탐색 유일값 검사 이런게 엄청 빠름

10^8 개 정도의 데이터가 있다면 높이는 3
4개의 디스크 페이지를 읽으면 찾을 수 있음 40 밀리세컨

만약 인덱스 없이 그냥 찾는다고 하면
페이지가 1억개면 1억개를 다 읽음 10억 미리세컨 100만초

해쉬 인덱스에서는 무작위로 골고루 나오게 해야 충돌이 덜 발생함