혼공 ML+DL #8

myeong·2022년 9월 22일

규제 다중 회귀

ML+DL

목록 보기

6/23

📌 다중 회귀 Multiple Regression

여러개의 특성을 사용 -> 길이, 높이, 무게
특성 추가, 변경, 조합 = 특성 공학

📍 판다스로 Data Set

csv 파일 -> 판다스 데이터 프레임 -> 넘파이 배열

import pandas as pd

df = pd.read_csv('https://bit.ly/perch_csv_data')
perch_full = df.to_numpy()
print(perch_full)

length, height, width
[[ 8.4 2.11 1.41]

[13.7 3.53 2. ]

[15. 3.82 2.43] ...]

from sklearn.model_selection import train_test_split

train_input, test_input, train_target, test_target = train_test_split(
	perch_full, perch_weight, random_state=42
)

📍 사이킷런의 변환기

fit() 으로 데이터를 입력받으면 어떻게 변환시킬지 파악
trainsform() 으로 데이터를 변환하여 새로운 특성을 생성
PolynomialFeatures의 기본 degree = 2 (제곱)

from sklearn.preprocessing import PolynomialFeatures

poly = PolynomialFeatures(include_bias=False)

poly.fit(train_input)
train_poly = poly.transform(train_input)

print(train_poly.shape)

(42, 9) // shape으로 (sample, feature) 크기 출력

poly.get_feature_names()  // 특성 생성 방식

['x0', 'x1', 'x2', 'x0^2', 'x0 x1', 'x0 x2', 'x1^2', 'x1 x2', 'x2^2']

📍 다중 회귀 모델 훈련

test_poly = poly.transform(test_input)

from sklearn.linear_model import LinearRegression

lr = LinearRegression()
lr.fit(train_poly, train_target)

print(lr.score(train_poly, train_target))
print(lr.score(test_poly, test_target))

0.9903183436982124 // 훈련 set
0.9714559911594134 // 테스트 set

📍 더 많은 특성 만들기

degree = 5 로 설정

poly = PolynomialFeatures(degree=5, include_bias=False)
poly.fit(train_input)
train_poly = poly.transform(train_input)
test_poly = poly.transform(test_input)

print(train_poly.shape)

(42, 55) // 특성 55개로 증가

lr.fit(train_poly, train_target)

print(lr.score(train_poly, train_target))
print(lr.score(test_poly, test_target))

0.9999999999991097 // 훈련 set
-144.40579242684848 // 테스트 set

-> 극도의 과대적합

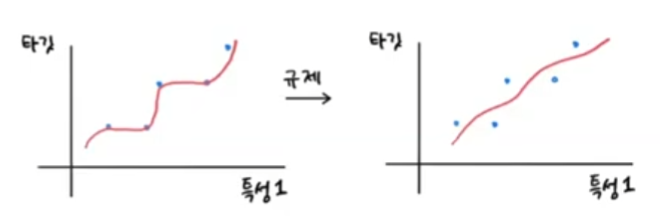
📌 규제 Regularization (정규화)

릿지 회귀 (선호) / 라쏘 회귀
극도의 과대적합을 완화. 훈련 set 에 과적합되는 것을 막음
가중치(기울기)를 줄여줌

📍 규제 전에 표준화 (변환) 필요

from sklearn.preprocessing import StandardScaler

ss = StandardScaler()
ss.fit(train_poly)

train_scaled = ss.transform(train_poly)
test_scaled = ss.transform(test_poly)

📍 릿지 회귀 Ridge Regression

L2 규제 : 가중치² 를 벌칙으로 사용
alpha 값에 비례하여 규제 강도 조절
가중치² : 모델 파라미터 / alpha : 하이퍼 파라미터

from sklearn.linear_model import Ridge

ridge = Ridge() # alpha = 1 (default)
ridge.fit(train_scaled, train_target)
print(ridge.score(train_scaled, train_target))
print(ridge.score(test_scaled, test_target))

0.9896101671037343 // 훈련 set
0.9790693977615391 // 테스트 set

📍 적절한 규제 강도 찾기

np.log10(alpha_list) 를 x 값으로 설정
0.001, 0.01 등 작은 변수 사이의 변화량을 가시적으로 표현

import matplotlib.pyplot as plt

train_score = []
test_score = []
alpha_list = [0.001, 0.01, 0.1, 1, 10, 100]

for alpha in alpha_list:
  ridge = Ridge(alpha= alpha)
  ridge.fit(train_scaled, train_target)
  train_score.append(ridge.score(train_scaled, train_target))
  test_score.append(ridge.score(test_scaled, test_target))

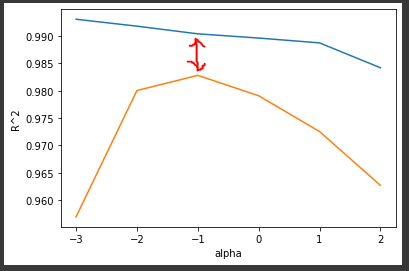
plt.plot(np.log10(alpha_list), train_score)
plt.plot(np.log10(alpha_list), test_score)
plt.xlabel('alpha')
plt.ylabel('R^2')
plt.show()

<-과대적합 ------------------------------ 과소적합->

훈련 set 그래프와 테스트 set 그래프의 차이가 작을수록 적합
👉 alpha = 0.1

📍 라쏘 회귀 Lasso Regression

L1 규제 : |가중치| 를 벌칙으로 사용
alpha 값에 비례하여 규제 강도 조절
일부 특성에 대한 가중치를 0으로 만들어서 아예 사용하지 않을 수도 있음

from sklearn.linear_model import Lasso

lasso = Lasso(alpha=10)
lasso.fit(train_scaled, train_target)

print(lasso.score(train_scaled, train_target))
print(lasso.score(test_scaled, test_target))
print(np.sum(lasso.coef_ == 0)) # 사용 안한 특성 갯수