✏️벡터

벡터(Vector)란?

• 공간에서의 한 점 - 1차원(수직선)에선 scalar, 2차원(좌표평면)에선 (x,y)축의 point
• 원점으로부터의 상대적 위치
• 벡터에 숫자를 곱하면 길이만 변한다.
• 두 벡터의 덧셈은 상대적 위치이동을 표현
• 뺄셈은 방향을 뒤집은 덧셈이다.
  
  
  

벡터의 norm이란?

• 원점에서부터의 거리
• 임의의 차원 d에 대해 성립
• L1-norm(Manhattan norm) : 각 성분 변화량의 절대값을 모두 더한다.

  $\left||x\right||_1 = \sum^d_{i=1}\left|x_i\right|$

• L2-norm(Euclidean norm) : 피타고라스의 정리를 이용, 유클리드 거리를 계산한다

  $\left||x\right||_2 = \sqrt{\sum^d_{i=1}\left|x_i\right|^2}$

두 벡터 사이의 거리

• L1, L2-norm 활용
• 벡터의 뺄셈을 이용 (뺄셈을 거꾸로 해도 거리는 같다.)

  $\left||y-x\right|| = \left||x-y\right||$

두 벡터 사이의 각도

• L2-norm으로만 구할 수 있다. (L1-norm으론 불가능) → 내적(정사영)을 이용한 계산이기 때문
• 제 2 코사인 법칙에 의해 두 벡터 사이의 각도를 계산할 수 있다.

  $cos\theta = {2<x,y>\over2\left||x\right||_2\left||y\right||_2}$, $<x,y> = \sum^d_{i=1}x_iy_i$

내적

• 두 벡터의 유사도(similarity) 측정 가능

  $<x,y> = \left||x\right||_2\left||y\right||_2cos\theta$

---

✏️행렬

행렬(Matrix)이란?

• 벡터를 원소로 가지는 2차원 배열 (반드시 행벡터를 원소로 가지는 2차원 배열로 인식해야 편하다)
• 벡터 표현: 소문자 볼드체, 행렬 표현: 대문자 볼드체
• 벡터공간에서 사용되는 연산자(operator)
  → 행렬곱을 통해 벡터를 다른 차원의 공간으로 보낼 수 있다
  → 패턴 추출, 데이터 압축 가능
  

행렬 곱셉(Matrix multiplication)

• i 번째 행벡터와 j 번째 열벡터 사이의 내적
• XY에서 X의 열의 개수와 Y의 행의 개수가 같아야 한다!(중요)
• numpy에서 @ 사용 ex) X @ Y
• numpy.inner() ≠ @ = numpy.dot()
  

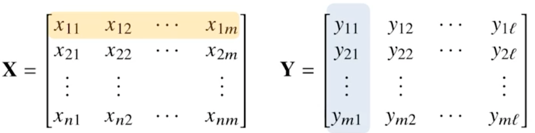
역행렬(Inverse Matrix)

1. 행과 열의 수가 같아야 존재
2. 행렬식(determinant)가 0이 아니어야 존재

   $AA^{-1} = A^{-1}A = I$

유사역행렬(pseudo-inverse) = 무어-펜로즈(Moore-Penrose) 역행렬

• 역행렬을 계산할 수 없을 때 이용 ex) n ≠ m

  $n \geqq m$인 경우, $A^+ = (A^TA)^{-1}A^T$  $A^+A = I$ 성립
  $n \leqq m$인 경우, $A^+ = A^T(A^TA)^{-1}$  $AA^+ = I$ 성립

---

✏️경사하강법(gradient descent)

미분(differentiation)이란?

• 변수의 움직임에 따른 함수값의 변화를 측정하기 위한 도구
• 최적화에서 제일 많이 사용하는 기법
• 연속함수(매끄러운 함수의 모양)에서 가능
• 한 점에서 접선의 기울기(=미분 값)를 알면 어느 방향으로 점을 움직여야 함수값이 증가/감소하는지 알 수 있다.
  → 증가시키고 싶다면 미분값을 더한다. = 경사상승법(gradient ascent)
  → 감소시키고 싶다면 미분값을 뺀다. = 경사하강법(gradient descent)
• 극값에 도달하면 움직임을 멈춘다 → 극값에선 미분값이 0이므로 업데이트 안 된다. 목적함수 최적화 자동종료

편미분(partial differentiation)이란?

• 벡터가 입력인 다변수 함수의 경우 사용
• 주어진 변수의 개수만큼 계산해 볼 수 있다.
• 한 변수의 방향으로만 변화, 나머지는 상수처리로 변화 X
• gradient vector : 각 변수 별로 편미분을 계산한 벡터

경사하강법 - 선형회귀분석

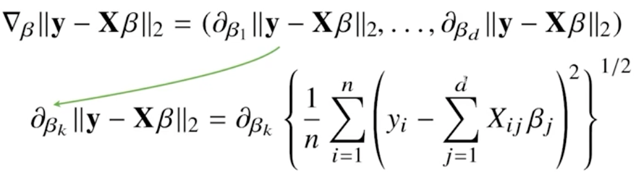
• β(coefficient)를 찾는 것이 선형회귀분석의 목적이기에, 목적식을 β로 미분, 주어진 β에서 미분값을 빼주면 경사하강법으로 최소값을 찾을 수 있다.
• L2-norm과 약간의 차이점 : 평균값을 계산하기 위해 1/n을 추가한다.

확률적 경사하강법(Stochastic gradient descent)

• 비선형(non-convex)한 함수에서는 gradient descent 수렴이 항상 보장되지 않는다.
• 데이터 한개 또는 일부 활용하여 경사하강을 진행

  데이터 모두 : Gradient Descent
  데이터 일부 : Mini-batch Stochastsic Gradient Descent (요즈음 가장 많이쓰이는 기법)
  데이터 한개 : Stochastic Gradient Descent (비효율적)

• 알고리즘 효율성과 리소스(하드웨어) 연산량 고려했을 때 아주 좋은 선택이다.
• 학습횟수(step)과 학습률(learning-rate) hyperparameter 초기설정 중요!