✏️통계학(Statistics)

모수(parameter)

• 통계적 모델링은 적절한 가정 위에서 확률분포를 추정(inference)하는 것이 목표
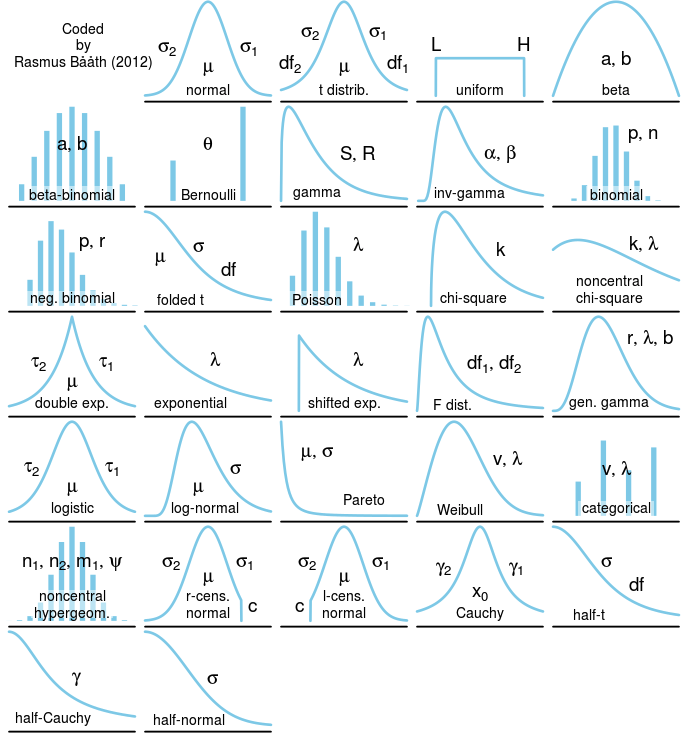  (출처 : https://priorprobability.com/2016/09/18/taxonomy-of-univariate-distributions/)
  
  
• 유한한 개수의 데이터만 관찰해서 모집단의 분포를 정확히 알아내는 것은 불가능 → 근사적으로 확률분포 추정
• 예측모형의 목적: 분포를 정확하게 맞추는 것 데이터와 추정 방법의 불확실성을 고려, 예측 위험 최소화
• ⭐️ 모수적(parametric) 방법론: 데이터가 특정 확률분포를 따른다고 선험적으로(a priori) 가정한 후 그 분포를 결정하는 모수(parameter)를 추정 ex) 정규분포의 중요한 모수 : 평균과 분산
• ⭐️ 비모수적(non-parametric) 방법론: 특정 확률분포를 가정하지 않고 데이터에 따라 모델의 구조 및 모수의 개수가 유연하게 바뀜(무수히 많다) → 비모수 방법론에도 모수는 존재

확률분포(Probability Distribution)

• 기계적으로 확률분포를 가정해서는 안된다.
• 데이터를 생성하는 원리를 먼저 고려하는 것이 원칙
• 각 분포마다 검정하는 방법 존재, 모수를 추정한 후에는 반드시 통계적 검증 필요
• 추정된 모수로 데이터의 성질 & 정보들을 취합해 예측 & 의사결정에 사용 가능

  정규분포 표본평균 : $\bar{X} = {1 \over N} \sum^N_{i=1}X_i$,     $\mathbb{E}[\bar{X}] = \mu$
  정규분포 표본분산 : $S^2 = {1 \over N-1} \sum^N_{i=1}\left(X_i-\bar{X}\right)^2$,     $\mathbb{E}[S^2] = \sigma^2$

• 표본분산 구할 떄 N이 아니라 N-1로 나누는 이유는 불편(unbiased) 추정량을 구하기 위해서이다.
  (출처: https://m.blog.naver.com/sw4r/221021838997)

표집분포(Sampling distribution)

• 통계량(표본평균/표본분산)의 확률분포
• ⭐️⭐️ 중심극한정리(Central Limit Theorem): 표본평균의 표집분포는 N이 커질수록 정규분포 $\mathcal{N}(\mu,\sigma^2/N)$ 를 따른다.
  → 모집단의 분포가 정규분포를 따르지 않아도 성립, 표본분포는 데이터를 많이 모아도 정규분포가 될 수 없다.
• 표집분포 ≠ 표본분포(표본들의 분포)