4장 에지와 영역

에지(edge)는 물체 경계에 있는 점이다.

💡 에지를 검출함으로서 물체의 위치, 모양, 크기 등에 대한 정보를 쉽게 찾을 수 있다.

4.1 에지 검출

에지 검출 알고리즘은 물체 내부는 명암이 서서히 변하고 물체 경계는 명암이 급격히 변하는 특성을 활용한다.

4.1.1 영상의 미분

미분은 변수 x의 값이 미세하게 증가했을 때 함수의 변화량을 측정한다. 미분 연산을 디지털 연상에 어떻게 적용할까? 정수 좌표를 쓰는 디지털 영상에서는 x의 최소 변화량이 1이므로 델타 x = 1로 한다.

4.1.2 에지 연산자

다음 사진은 필터 u = ( -1, 1)로 컨볼루션 한 결과이다. 1차 미분은 에지가 어떤 방향을 향하는지(양수, 음수)에 대한 정보를 제공하지만 에지의 정확한 위치를 정하는 위치 찾기 문제가 생겼다.

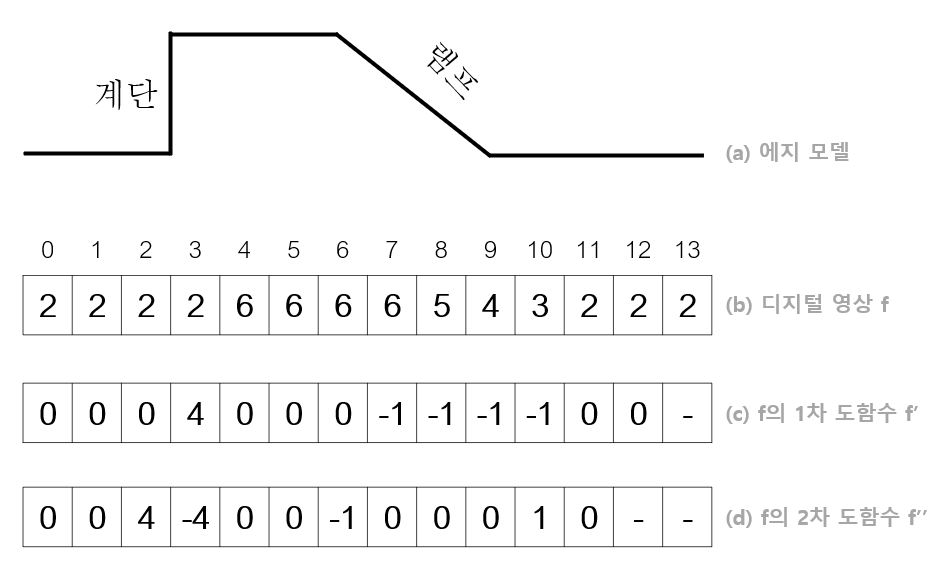
u로 컨볼루션한 영상을 u로 한 번 더 컨볼루션하면 원래 영상을 두 번 미분한 2차 미분 영상 f’’로 볼 수 있다.

1차 미분 영상에서는 봉우리가 발생하고 2차 미분 영상은 영교차가 발생한다. 영교차란 왼쪽과 오른쪽에 부호가 다른 반응이 나타나고 자신은 0을 갖는 위치를 뜻한다.

💡 에지 검출은 1차 미분에서 봉우리를 찾거나 2차 미분에서 영교차를 찾는 일이라고 정의할 수 있다.

에지 연산자 (-1, 1)은 너무 작고 대칭이 아니다. ( -1, 0, 1)로 확장해서 사용한다.

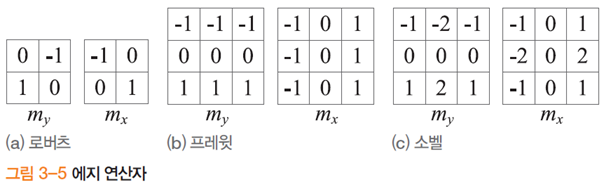
소벨이 가장 많이 쓰인다.

4.2 캐니 에지

캐니 에지는 에러율이 낮다는 장점이 있지만 구현이 복잡하고 수행 시간이 길다.

import cv2 as cv

img = cv.imread('soccer.jpg')
gray = cv.cvtColor(imag, cv.COLOR_BGR2GRAY)

canny1 = cv.Canny(gray, 50, 150)
canny2 = cv.Canny(gray, 100, 200)

cv.imshow('Canny1', canny1)
cv.imshow('Canny2', canny2)

다음은 예시 코드이다. 캐니 알고리즘은 거짓 긍정을 줄이기 위해 2개의 이력 임곗값 T(low), T(high)를 이용한 에지 추적을 추가로 적용한다. 거짓 긍정이란 실제 에지가 아닌데 에지로 검출된 화소를 뜻한다. 캐니는 T(high)를 T(low)의 2~3배로 설정할 것을 권고했다.

4.3 직선 검출

앞에서 에지로 검출된 에지 화소는 1, 에지가 아닌 화소는 0으로 표시한다. 이들을 연결하여 경계선으로 반환하고 경계선을 직선으로 변환하면 이후 단계인 물체 표현이나 인식에 무척 유리하다.

4.3.1 경계선 찾기

에지 맵에서 이웃한 에지를 연결하여 경계선을 검출한다.(p.128 ~ 129)

4.3.2 허프 변환

허프변환은 이미지에서 모양을 찾는 가장 유명한 방법이다. 에지를 연결하여 경계선을 검출하는 방법은 에지가 자잘하게 끊겨 나타나는 경우 문제가 발생한다. 이런 상황에 허프 변환을 적용하여 끊긴 에지를 모아 선분 또는 원 등을 검출할 수 있다.

한 점을 지나는 직선은 다음과 같이 표현할 수 있습니다.

그럼 각 점(x,y)에 대해서 삼각함수를 이용하여 𝜃 값을 1 ~ 180까지 변화를 하면서 원점에서 (x,y)까지의 거리(r)을 구합니다. 그러면 (𝜃, r)로 구성된 180개의 2차원 배열을 구할 수 있다. 동일한 방법으로 두번째 점에 대해서도 𝜃값을 변화해 가면서 2차원 배열을 구한다.

💡 edge를 모아 직선인 확률이 가장 높은 직선을 구한다.

허프 변환 — gramman 0.1 documentation

위 설명을 참고했습니다.

4.3.3 RANSAC

데이터 분포로부터 현저히 벗어난 점을 outlier라고 한다. 허브 변환, 최소제곱평균오차(MSE)는 outlier가 섞여 있는 데이터셋에서는 좋은 성능을 발휘하지 못한다.

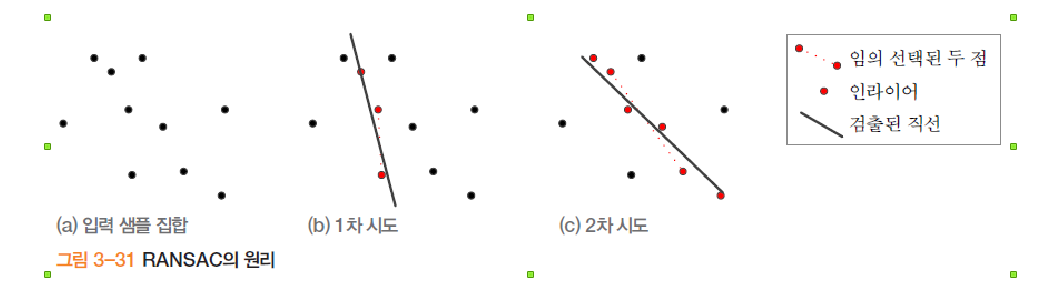
Hypothesis - 가설 단계

전체 데이터에서 N개의 샘플을 선택하고, 선택된 샘플을 통해 모델을 예측한다.

Verification - 검증단계

데이터셋에서 모델과 일치하는 데이터의 수를 센 후, 최대 값일 경우 모델 파라미터를 새롭게 저장한다.

💡 위 두 단계를 N번 반복하며, 그 중 최고의 모델을 출력해준다.

4.4 영역 분할

영역 분할은 물체가 점유한 영역을 구분해주는 작업이다. 에지가 완벽하다면 영역 분할이 필요하지 않지만 명암 변화가 낮은 곳에서 뚫려 폐곡선을 형성하지 못하는 경우 많다.

4.4.1 배경이 단순한 영상의 영역 분할

Watershed는 비가 오면 오목한 곳에 웅덩이가 생기는 현상을 모방하는 연산이다. 워터세드를 확장해 영역 분할에 활용할 수 있다.

[Image Processing] Watershed(워터쉐드) 적용하기

4.4.2 슈퍼 화소 분할

때론 영상을 아주 작은 영역으로 분할해 다른 알고리즘의 입력으로 사용하는 경우가 있다. 작은 영역은 화소보다 크지만 물체보다 작기 때문에 슈퍼 화소라 한다.

SLIC 알고리즘

k-means clustering과 유사하게 작동한다. (R, G, B, x, y)로 5차원 벡터를 형성하고 군집 중심 C(n)을 군집 중심이 물체 경계에 놓이지 않도록 그레디언트가 가장 낮은 이웃 화소로 이동시킨다. 화소 각각에 대해 주위 4개 군집 중심(k=8인 경우)과 자신까지 거리를 계산해서 가장 유사한 군집 중심에 할당한다. 화소 할당이 끝나면 각 군집 중심은 자신에게 할당된 화소를 평균해 군집 중심을 갱신한다. 모든 군집 중심의 이동량의 평균을 구하고 평균이 임계치보다 작으면 수렴했다고 판단하고 알고리즘을 멈춘다.

[머신러닝] K-평균(K-Means) 알고리즘

4.4.3 최적화 분할

앞선 알고리즘은 지역적 명암 변화만 살핀다. 배경색과 물체의 색이 비슷한 경우 경계가 형성되지 않을 수 있다. 이 문제를 해결하기 위해 지역적 명암 변화를 보되 전역적 정보를 같이 고려하는 방법을 사용한다. 이 방법을 사용하기 위해서는 주로 영상을 그래프로 표현하고 분할을 최적화 문제로 푼다.

앞서 언급한 5차원 벡터 v = (R, G, B, x, y) 사이의 거리가 사용자가 지정한 r 이내면 참이다.

정규화 절단 알고리즘: cut(C1, C2)라는 함수를 사용해 영역 분할의 좋은 정도를 측정한다.

4.5 대화식 분할

지금까지 다룬 분할 알고리즘은 영상 전체를 여러 영역으로 나눈다. 한 물체의 분할에만 관심이 있는 경우 초기 정보를 가지고 사용자의 의도에 맞게 물체를 분할한다.

4.5.1 능동 외각선

사용자가 물체 내부에 초기 곡선을 지정하면 곡선을 점점 확장하면서 물체 외곽선으로 접근하는 방법이다. 곡선이 꿈틀대면서 에너지가 최소인 상태를 찾아가기 때문에 스네이크라는 별명을 얻었다.

4.5.2 GrabCut

GrabCut 알고리즘은 이미지에서 배경이 아닌 전경에 해당하는 이미지를 추출해 내는 방법이다. 이미지에서 한번에 전경을 추출해 내는 것이 아닌 사용자와의 상호 작용을 통해 단계적으로 전경을 추출한다. 이 상호작용은 크게 2가지 단계로 진행되는데, 첫번째는 이미지에서 전경이 포함되는 영역을 사각형으로 대략적으로 지정한다. 그리고 두 번째는 첫 번째에서 얻어진 전경 이미지의 내용중 포함되어진 배경 부분은 어디인지, 누락된 전경 부분은 어디인지를 표시하면 이를 이용해 다시 전경 이미지가 새롭게 추출된다.

4.6 영역 특징

텍스처 특징

텍스처는 영상의 질감(반복되는 일정 패턴)이다. 텍스처가 세밀하면 많은 에지가 발생하고 거칠면 적게 발생한다. busy는 에지 화소 수를 전체 화소 수로 나누어 세밀함을 측정한다. mag는 에지 강도를 q 단계로 양자화하여 구한 히스토그램이고 dir은 에지 방향을 8단계로 양자화해 구한 히스토그램이다.

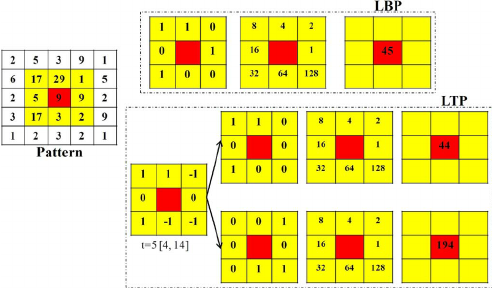
LBP(local binary pattern)는 빨간색 화소보다 큰 화소는 1 작은 화소는 0으로 표시한다.

LTP(local tenary pattern) (빨간색 화소 - 임계값 t)보다 작은 화소 -1 큰 화소 1

💡 컴퓨터 비전과 딥러닝 책을 요약한 내용입니다. 코드는 책을 참고해주세요 😀