Training Models

최승훈·2023년 10월 1일

머신러닝 모델과 그들의 훈련 알고리즘을 대부분 black box처럼 취급했습니다. ch03을 통해 어떻게 했는지 모르고도 회귀 시스템을 최적화하고, 숫자 이미지 분류기를 개선하고, 심지어 스팸 분류기를 처음부터 구축할 수 있었던 것이 놀라웠습니다. 실제로 많은 상황에서는 구현 세부 사항을 알 필요가 없다고 합니다.

그러나 어떻게 작동하는지 이해하는 것이 적절한 모델, 사용할 훈련 알고리즘 및 작업을 위한 좋은 하이퍼파라미터 세트를 빠르게 찾을 수 있게 도와줍니다. 내부 작동 원리를 이해하면 문제를 디버깅하고 오류 분석을 더 효율적으로 수행하는 데도 도움이 됩니다. 마지막으로 이 장에서 논의되는 대부분의 주제는 신경망을 이해하고, 구축하고, 훈련시키는 데 필수적일 것입니다.

1. Linear Regression

선형 모델은 입력 특성의 가중합을 계산함으로써 예측을 수행하며, 이때 상수항인 편향 항을 더합니다.
Linear model prediction formula:

y = \theta_0 + \theta_1 x_1 + \theta_2 x_2 + \ldots + \theta_n x_n

Vectorized form of Linear model prediction formula:

y = h_\theta(\mathbf{x}) = \theta^T \cdot \mathbf{x}

모델을 훈련시키는 것은 모델이 훈련 세트에 최적으로 적합하도록 그 파라미터를 설정하는 것을 의미합니다. 우리는 먼저 모델이 훈련 데이터에 얼마나 잘 (또는 얼마나 나쁘게) 적합하는지 측정할 필요가 있습니다.

루트 평균 제곱 오차 (Root Mean Square Error, RMSE)
따라서, 선형 회귀 모델을 훈련시키려면 RMSE를 최소화하는 θ의 값을 찾아야 합니다. 실제로는 RMSE를 최소화하는 것보다 평균 제곱 오차 (Mean Squared Error, MSE)를 최소화하는 것이 더 간단하며, 이는 동일한 결과를 이끌어냅니다.

The Normal Equation

Normal Equation은 비용 함수를 최소화하는 θ의 값을 직접 찾아주는 수학적 방정식입니다.

\boldsymbol{\theta} = (\mathbf{X}^T \mathbf{X})^{-1} \mathbf{X}^T \mathbf{y}

하지만 역행렬이 없는 행렬도 있습니다. 그런 경우 pseudo inverse를 사용하여 역행렬을 계산합니다.

\boldsymbol{\theta} = \mathbf{X}^+ \mathbf{y}

유사 역행렬 자체는 특이값 분해(Singular Value Decomposition, SVD)라는 표준 행렬 분해 기법을 사용하여 계산됩니다.

Computational Complexity

정규 방정식은 X^T * X의 역행렬을 계산합니다. 이는 (n + 1) × (n + 1) 행렬입니다 (여기서 n은 특성의 수입니다). 이러한 행렬의 역행렬을 구하는 계산 복잡도는 대략 ( O(n^{2.4}) )에서 ( O(n^3) ) 사이로, 구현에 따라 달라집니다. 다시 말해, 특성의 수를 두 배로 늘리면, 계산 시간은 대략 ( 2^{2.4} = 5.3 )에서 ( 2^3 = 8 )까지 곱해집니다.

Scikit-Learn의 LinearRegression 클래스에서 사용하는 SVD(특이값 분해) 접근법은 대략 ( O(n^2) )입니다.
- 특성의 수를 두 배로 늘리면, 계산 시간은 대략 4배가 됩니다.
특성의 수가 많아질 때 (예: 100,000개), 정규 방정식과 SVD 접근법 모두 매우 느려집니다.
- 긍정적인 측면으로, 두 방법 모두 훈련 세트의 인스턴스 수에 대해 선형적이므로 (즉, O(m), 메모리에 맞는 한 큰 훈련 세트를 효율적으로 처리할 수 있습니다.

2. Gradient Descent

이제 선형 회귀 모델을 훈련시키는 매우 다른 방법을 살펴볼 것입니다. 이 방법은 특성의 수가 많거나 메모리에 맞지 않을 정도로 많은 훈련 인스턴스가 있는 경우에 더 적합합니다.

경사 하강법은 다양한 문제에 대한 최적의 해를 찾을 수 있는 일반적인 최적화 알고리즘입니다. 경사 하강법의 일반적인 아이디어는 비용 함수를 최소화하기 위해 매개변수를 반복적으로 조정하는 것입니다. 이 방법은 매개변수 벡터 θ에 대한 오류 함수의 지역 기울기를 측정하고, 기울기가 감소하는 방향으로 진행합니다. 기울기가 0이 되면 최솟값에 도달한 것입니다!

먼저 θ를 랜덤 값으로 채웁니다(이것을 랜덤 초기화라고 합니다). 그런 다음 점진적으로 개선하며, 한 번에 한 걸음씩 걸으며, 각 단계에서 비용 함수(예: MSE)를 줄이려고 시도합니다, 알고리즘이 최소값에 수렴할 때까지 이어집니다.

학습률(Learning Rate)

걸음의 크기를 나타냅니다. 학습률이 너무 작으면 알고리즘이 수렴하기 위해 많은 반복을 거쳐야 하며, 이는 시간이 많이 걸립니다. 반면에, 학습률이 너무 높으면 계곡을 건너뛰어 반대편에 도달하게 되어 알고리즘이 발산할 수 있습니다.

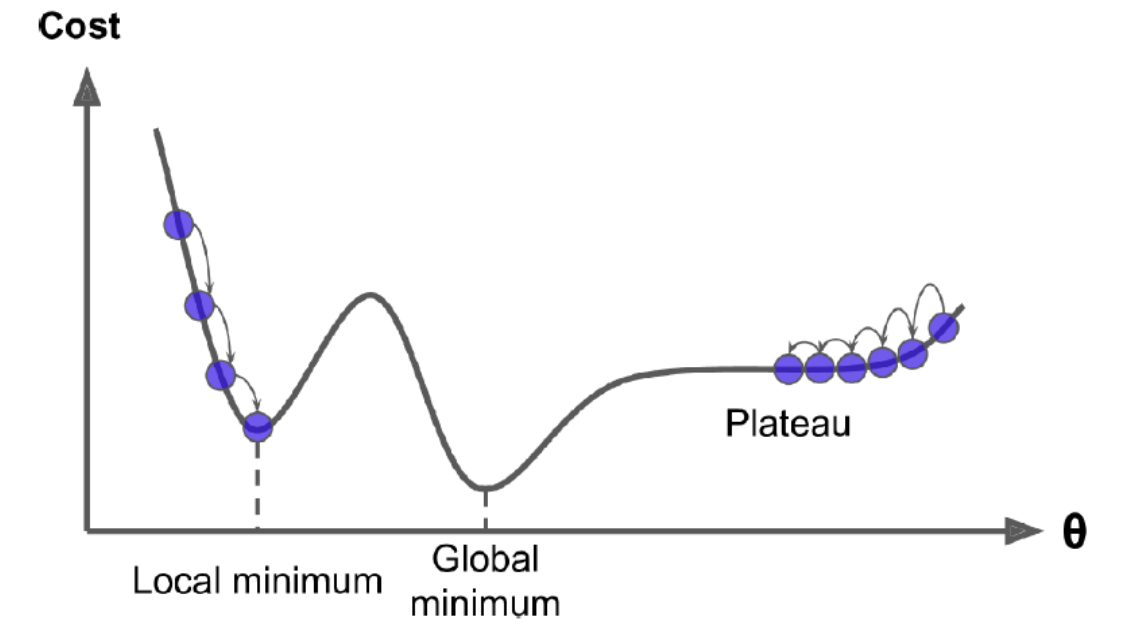
구멍, 가장자리, 고원 및 모든 종류의 불규칙한 지형이 있을 수 있어 최소값에 수렴하는 것이 어렵게 만듭니다. 랜덤 초기화가 알고리즘을 왼쪽으로 시작하면 지역 최소값에 수렴하게 되며, 이는 전역 최소값만큼 좋지 않습니다.오른쪽에서 시작하면 고원을 가로질러 가는 데 매우 오랜 시간이 걸립니다. 그리고 너무 일찍 멈추면 전역 최소값에 도달하지 못합니다.

선형 회귀 모델의 MSE 비용 함수는 볼록 함수(bowl)라는 것이 밝혀졌습니다, 이는 곡선 상의 어떤 두 점을 선택하더라도 그들을 연결하는 선분이 곡선을 건너지 않는다는 것을 의미합니다.

이는 지역 최소값이 없고 단 하나의 전역 최소값만 있다는 것을 의미합니다. 또한 갑작스럽게 변하지 않는 기울기를 가진 연속 함수입니다.비용 함수가 볼록할 때, 경사 하강법은 긴 시간동안 기다리고 학습률이 너무 높지 않다면 전역 최소값에 임의로 접근할 것이 보장됩니다.

실제로, 비용 함수는 그릇의 형태를 가지고 있지만, 특성들의 스케일이 매우 다르다면 길쭉한 그릇의 형태를 가질 수 있습니다.

경사 하강법을 사용할 때, 모든 특성이 유사한 스케일을 가지도록 확인해야 합니다(예: Scikit-Learn의 StandardScaler 클래스를 사용함), 그렇지 않으면 수렴하는 데 훨씬 더 오랜 시간이 걸립니다.

Batch Gradient Descent

Gradient Descent에 Dataset 전체를 넣는 것을 Batch Gradient Descent라고 합니다. 경사 하강법을 구현하기 위해서는 각 모델 파라미터 Θ에 대한 비용 함수의 그래디언트를 계산해야 합니다. 다시 말해, Θ를 조금 변경하면 비용 함수가 얼마나 변할지 계산해야 합니다. 이것을 편미분이라고 합니다.

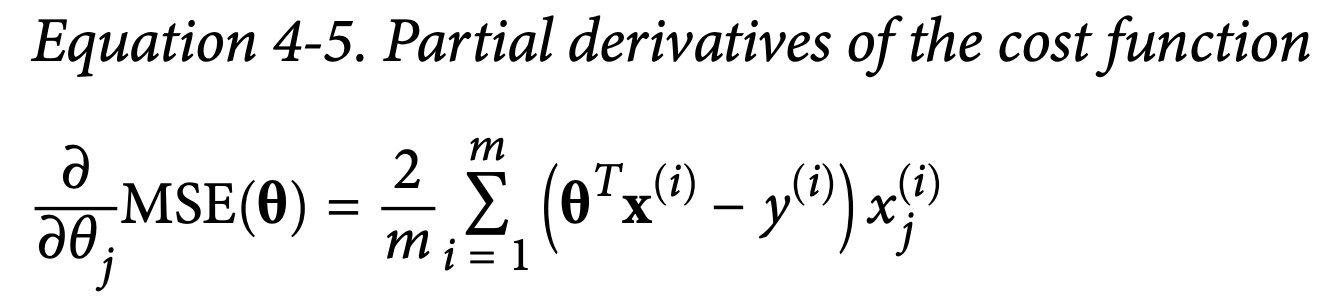
이 공식은 각 경사 하강법 단계에서 전체 훈련 세트 X에 대한 계산을 포함하고 있습니다. 이것이 알고리즘이 배치 경사 하강법(Batch Gradient Descent)이라고 불리는 이유입니다: 이 알고리즘은 각 단계에서 훈련 데이터의 전체 배치를 사용합니다.

이 알고리즘은 매우 큰 훈련 세트에서 무척 느립니다. 그러나 경사 하강법은 특성의 수에 대해 잘 확장되므로, 수십만 개의 특성이 있을 때 선형 회귀 모델을 훈련시키는 것은 정규 방정식(Normal Equation)이나 SVD 분해를 사용하는 것보다 경사 하강법을 사용하여 훈련시키는 것이 훨씬 빠립니다.

학습률이 너무 낮으면 알고리즘이 중지될 때 최적 해에서 여전히 멀리 떨어져 있을 것입니다. 너무 높으면 모델 매개변수가 더 이상 변경되지 않는 동안 시간을 낭비하게 됩니다.

간단한 해결책은 반복 횟수를 매우 크게 설정하지만, 기울기 벡터가 아주 작아질 때 즉, 아주 작은 수 ϵ보다 작아질 때 알고리즘을 중단시키는 것입니다. 이것은 경사 하강법이 (거의) 최소값에 도달했을 때 발생합니다.
배치 경사 하강법의 주요 문제점은 각 단계에서 기울기를 계산하기 위해 전체 훈련 세트를 사용한다는 사실로, 훈련 세트가 클 때 이것이 매우 느려집니다.

Stochastic Gradient Descent

확률적 경사 하강법(Stochastic Gradient Descent)은 각 단계에서 훈련 세트에서 무작위로 인스턴스를 선택하고 그 단일 인스턴스에만 기반하여 기울기를 계산합니다.

분명히 한 번에 하나의 인스턴스만 처리하면 알고리즘이 훨씬 더 빨라집니다. 왜냐하면 각 반복에서 조작할 데이터가 매우 적기 때문입니다.
또한 매 반복에서 메모리에 하나의 인스턴스만 있어야 하므로 거대한 훈련 세트에서 훈련시킬 수 있게 됩니다.

반면에, 그 확률적(즉, 무작위) 특성 때문에 이 알고리즘은 배치 경사 하강법보다 훨씬 덜 규칙적입니다: 최소값에 도달할 때까지 부드럽게 감소하는 대신 비용 함수는 위아래로 튀어 오르며 평균적으로만 감소하게 됩니다.

학습률을 점차 줄여나가기

스텝은 처음에 크게 시작하여(빠른 진행을 돕고 지역 최저점에서 벗어날 수 있도록 돕습니다) 점점 작아져서 알고리즘이 전역 최저점에 정착할 수 있게 됩니다. 각 반복에서 학습률을 결정하는 함수를 학습 일정(learning schedule)이라고 합니다.

학습률을 너무 빨리 줄이면 지역 최저점에 갇히게 되거나 최저점까지 도달하다가 중간에 멈출 수 있습니다. 학습률을 너무 천천히 줄이면 최저점 주변을 오랫동안 돌게 되고, 너무 일찍 훈련을 중단하면 최적이 아닌 해결책에 도달하게 될 수 있습니다.

주의할 점은 인스턴스들이 무작위로 선택되기 때문에, 어떤 인스턴스들은 에포크당 여러 번 선택될 수 있으며, 반면에 다른 인스턴스들은 전혀 선택되지 않을 수 있습니다.

알고리즘이 각 에포크에서 모든 인스턴스를 거치도록 하려면, 다른 접근 방법은 훈련 세트를 셔플하고, 인스턴스별로 거쳐가며, 다시 셔플하고, 계속해서 진행하는 것입니다. 확률적 경사 하강법을 사용할 때, 훈련 인스턴스들은 독립적이고 동일하게 분포되어야(IID) 평균적으로 매개변수가 전역 최적점을 향해 당겨질 것을 보장합니다.

Mini-batch Gradient Descent

미니 배치 경사 하강법(Mini-batch GD)은 미니 배치라고 불리는 작은 무작위 인스턴스 집합에 대해 기울기를 계산합니다. 미니 배치 경사 하강법의 주요 장점은 행렬 연산의 하드웨어 최적화로부터 성능 향상을 얻을 수 있으며, 특히 GPU를 사용할 때 유용하다는 것입니다.
이 알고리즘의 매개변수 공간에서의 진행은 확률적 경사 하강법(Stochastic GD)보다 덜 불규칙적이며, 특히 상당히 큰 미니 배치에서 그러합니다.

배치 경사 하강법(Batch GD)의 경로는 실제로 최소값에서 정지합니다. 확률적 경사 하강법과 미니 배치 경사 하강법은 계속해서 최소값 주변을 돌아다닙니다.

그러나 좋은 학습 스케줄을 사용해도 배치 경사 하강법은 각 단계를 수행하는 데 많은 시간이 소요됩니다.

3. Polynomial Regression

당신의 데이터가 직선보다 복잡하다면 어떻게 될까요?

비선형 데이터에 선형 모델을 사용하여 적합시킬 수 있습니다.
이를 수행하는 간단한 방법은 각 특성의 거듭제곱을 새로운 특성으로 추가하고, 이 확장된 특성 세트에 선형 모델을 학습시키는 것입니다.

여러 특성이 있을 때, 다항 회귀는 특성 간의 관계를 찾을 수 있습니다.

이는 PolynomialFeatures가 주어진 차수까지의 모든 특성 조합을 추가하기 때문에 가능합니다.
예를 들어, 두 특성 𝑎와 𝑏가 있다면, degree=3인 PolynomialFeatures는 𝑎^2, 𝑎𝑎^3, 𝑏^2, 𝑏^3 특성만 추가하는 것이 아니라 조합된 특성인 𝑎^1𝑏𝑏, 𝑎^2𝑏, 𝑎𝑏^2도 추가합니다.
PolynomialFeatures(degree=d)는 𝑛개의 특성을 포함하는 배열을 (𝑛 + 𝑑) !/ 𝑑! 𝑛!의 특성을 포함하는 배열로 변환합니다.
특성의 조합 수가 조합적으로 폭발할 수 있으므로 주의해야 합니다!

underfitting

모델이 과소적합되었을 때, 초기에는 제대로 일반화하지 못해 validation error가 큽니다. 모델에 더 많은 데이터를 제공하면 오류가 줄어들지만, 데이터를 올바르게 모델링하는 데는 한계가 있습니다. 이러한 과소적합의 특징은 두 곡선이 높은 곳에서 고원을 이루는 것으로 나타납니다.

overfitting

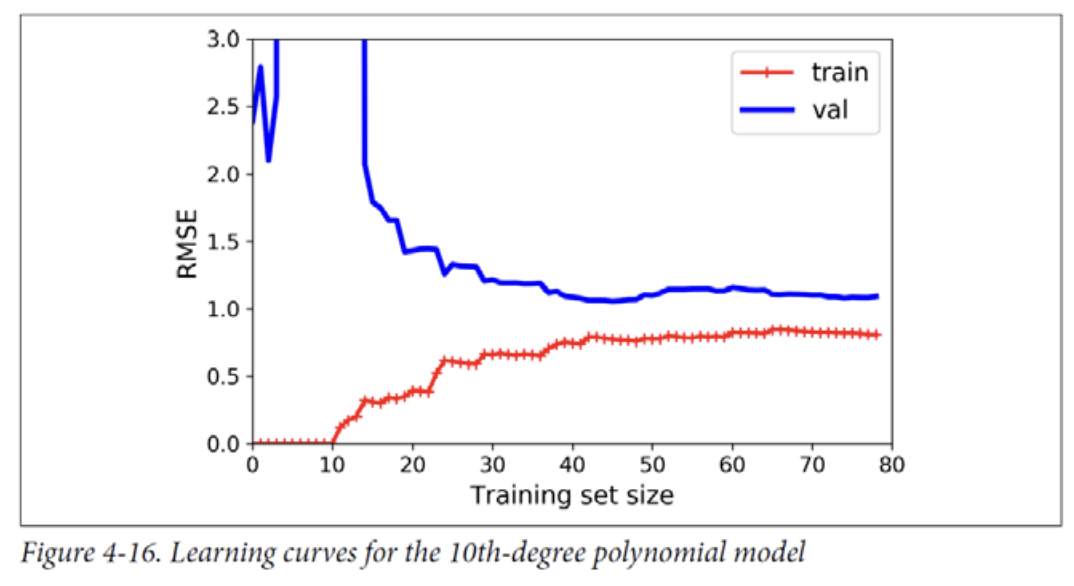
새로운 모델은 훈련 데이터에 대한 오류가 선형 회귀 모델보다 낮고, 훈련 데이터와 검증 데이터 간의 성능 차이가 나타나는데, 이는 과대적합의 특징입니다.

5. Regularized Linear Models

Regularization

A good way to reduce overfitting is to regularize the model (Fewer degree of freedom)
1. reducing training data error 2. simple model with fewer error

A simple way to regularize a polynomial model is to reduce the number of polynomial degrees.
For a linear model, regularization is typically achieved by constraining the weights of the model.

Ridge Regression

J(\theta) = MSE(\theta) + \alpha \sum_{i=1}^{n} \theta_i^2

alpha increase -> flatten

It is important to scale the data (e.g., using a StandardScaler) before performing Ridge Regression

Lasso Regression

J(\theta) = MSE(\theta) + \alpha \sum_{i=1}^{n} |\theta_i|

Add a regularization term to the cost function, but it uses the ℓ1 norm of the weight vector instead of half the square of the ℓ2 norm. An important characteristic of Lasso Regression is that it tends to eliminate the weights of the least important features (i.e., set them to zero).

Elastic net

Elastic Net is a middle ground between Ridge Regression and Lasso Regression.

J(\theta) = MSE(\theta) + \alpha \rho \sum_{i=1}^{n} |\theta_i| + \frac{\alpha (1-\rho)}{2} \sum_{i=1}^{n} \theta_i^2

Early Stopping

A very different way to regularize iterative learning algorithms such as Gradient Descent is to stop training as soon as the validation error reaches a minimum.

6. Logistic Regression

Commonly used to estimate the probability that an instance belongs to a particular class

Just like a Linear Regression model, a Logistic Regression model computes a weighted sum of the input features (plus a bias term), but instead of outputting the result directly like the Linear Regression model does, it outputs the logistic of this result

Training and cost function

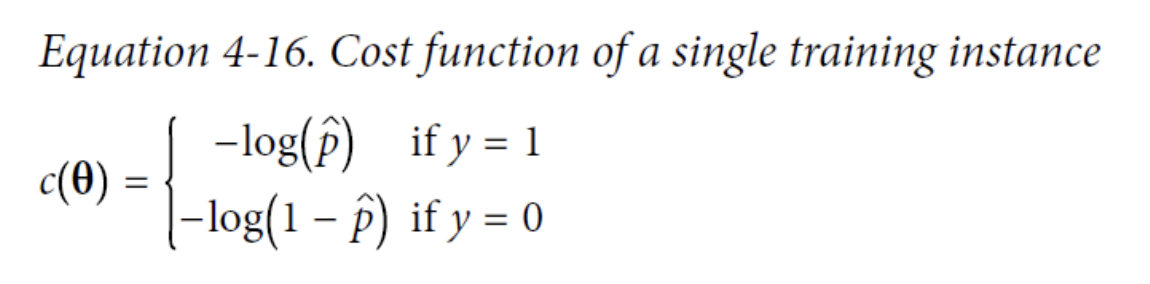
-log(t) grows very large when t approaches 0, so the cost will be large if the model estimates a probability close to 0 for a positive instance, and it
will also be very large if the model estimates a probability close to 1 for a negative instance.

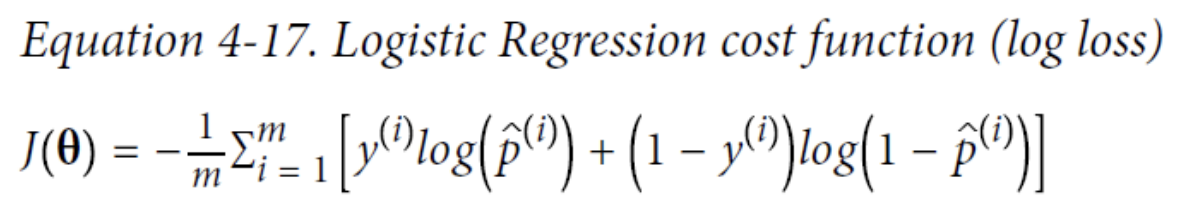
The bad news is that there is no known closed-form equation to compute the value of θ that minimizes this cost function (there is no equivalent of the Normal Equation). The good news is that this cost function is convex, so Gradient Descent (or any other optimization algorithm) is guaranteed to find the global minimum (if the learning rate is not too large and you wait
long enough).

Softmax Regression

The Logistic Regression model can be generalized to support multiple classes directly, without having to train and combine multiple binary classifiers.

When given an instance x, the Softmax Regression model first computes a score 𝑠𝑘(𝐱) for each class k, then estimates the probability of each class by applying the softmax function (also called the normalized exponential) to the scores.