[논문 정리] Deep Image Prior

https://arxiv.org/pdf/1711.10925

---

1. Introduction

• 최신 image reconstruction 문제들(denoising, super-resolution 등)은 deep convolutional neural network를 기반으로 함
• ConvNet은 대규모 데이터셋에서 학습되며, 좋은 성능이 데이터를 통해 학습된 것처럼 보이지만, 최근 연구에서는 network가 randomized label을 학습할 때도 overfitting 할 수 있음을 보여줌
• 이는 좋은 성능이 단순히 데이터 학습만으로는 설명되지 않으며, network 구조가 데이터 구조와 공명해야 함을 시사
• 본 연구에서는 ConvNet이 데이터를 통해 priors(사전 지식)를 반드시 학습할 필요가 없음을 보여줌
• ConvNet의 구조 자체가 학습 없이도 image 통계를 포착할 수 있으며, 이는 특히 image restoration 문제에서 중요한 역할을 함
• 본 연구에서는 학습되지 않은 ConvNet을 사용해, 대규모 image 데이터셋 대신 하나의 손상된 image에 network를 맞추는 방식으로 restoration을 수행
• 이 방식에서 network의 weight는 무작위로 초기화된 후 손상된 image에 맞춰 최적화
• 이를 통해 restoration 작업을 수행할 때 필요한 정보는 단일 손상된 image와 network 구조 자체에 내재된 priors 뿐임
• 이 간단한 방식이 denoising, inpainting, super-resolution, detail enhancement와 같은 image 처리 문제에서 매우 경쟁력 있는 성능을 보임
• 이는 데이터에서 학습되지 않았음에도 불구하고 network 구조가 image priors를 암묵적으로 포착함을 보여줌

Main Contribution

• Demonstrating the Effectiveness of Untrained ConvNets
  • 데이터를 학습하지 않은 ConvNets가 구조만으로도 image 통계를 포착할 수 있음을 증명
• Solving Restoration Problems
  • 학습 없이도 ConvNets 구조만으로 denoising, inpainting, super-resolution, detail enhancement와 같은 image restoration 문제를 해결
• Understanding Deep Network Activation
  • 분류에 학습된 deep network의 activation 값을 분석하는 응용 사례를 제시하여, 학습된 priors 없이도 network 구조가 natural image를 효과적으로 restoration 할 수 있음을 입증

---

2. Method

Deep Generator Network

• Deep generator network는 code vector $z$를 image $x$로 매핑하는 function $x = f_\theta(z)$로 표현
• 일반적으로 network는 복잡한 image 분포 $p(x)$를 간단한 분포 $p(z)$, 예를 들어 Gaussian 분포를 code로 변환하여 모델링

Capturing Information in Untrained Networks

• Network parameter $\theta$는 데이터에서 학습되지 않지만, 본 논문에서는 학습 없이도 network 구조가 image의 low-level 통계를 포착할 수 있음을 보여줌
• 특히 ConvNet 구조는 local 및 translation invariance를 통해 pixel 간 관계를 여러 scale에서 모델링할 수 있음

Energy Minimization Problem

• Image restoration 문제는 다음과 같은 energy minimization 문제로 정의:

  $x^* = \arg\min_x E(x; x_0) + R(x)$

• $E(x; x_0)$는 손상된 image $x_0$와 restoration 된 image $x$ 간의 data term
  • Restoration 된 image $x$와 손상된 이미지 $x_0$ 사이의 차이를 측정하는 loss function
  • 주로 L2 distance(Euclidean distance) 또는 L1 distance를 사용하여 두 이미지 간의 차이를 계산
• $R(x)$는 regularizer term
  • Restoration 된 image가 자연스럽고 부드러운 형태를 유지하도록 제약을 추가하는 역할
  • 예를 들어, Total Variation (TV)나 L2 regularizer가 자주 사용

Implicit Regularization

• 본 연구에서는 명시적인 regularizer term $R(x)$ 대신, network parameterization에 내재된 암묵적 prior을 활용하여 restoration 문제를 해결
• 이를 수식으로 표현하면:

  $\theta^* = \arg\min_\theta E(f_\theta(z); x_0), x^* = f_{\theta^*}(z)$

• 여기서 $f_\theta(z)$는 손상된 image $x_0$를 기반으로 network가 생성한 image이며, 최적화된 parameter $\theta^*$는 손상된 image를 restoration 하는데 사용

Deep Image Prior (DIP)

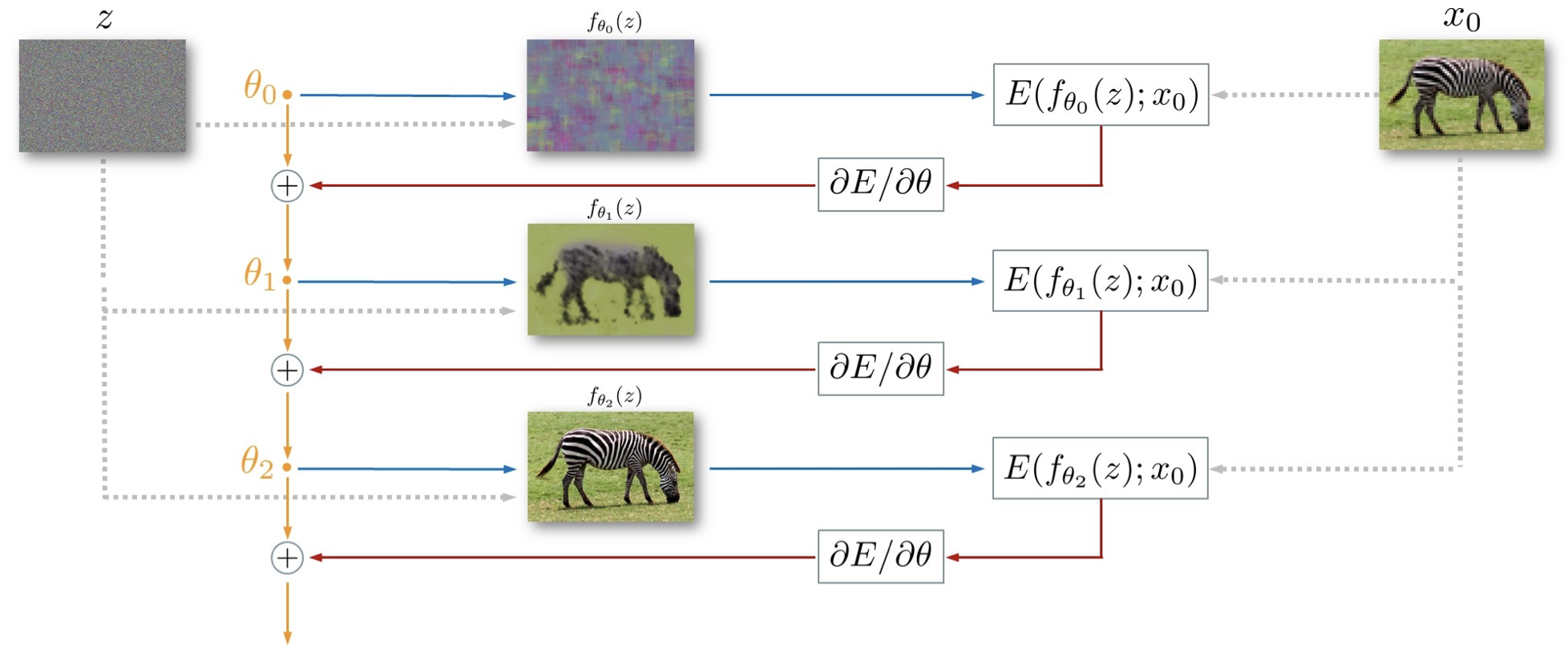
• Random noise($z$)로 시작: 처음엔 noise image처럼 보이는 tensor에서 시작
• Initial weight($\theta_0$)로 image 생성: 무작위로 초기화된 weight로 image를 만들면, 처음엔 noise 같은 image가 나옴
• Loss calculation: 생성된 image와 target image($x_0$)를 비교해서 loss function $E$를 계산
• Weight update: loss 값을 줄이기 위해 gradient descent로 weight를 업데이트
• Iteration: 이 과정을 여러 번 반복하면서, 생성된 image는 점점 원본 image에 가까워짐
• 결국, 데이터를 학습하지 않고도 network가 원본에 가까운 image를 restoration 할 수 있다는 것을 보여주는 과정

Visualization of Prior's Role in Image Restoration: Two Cases

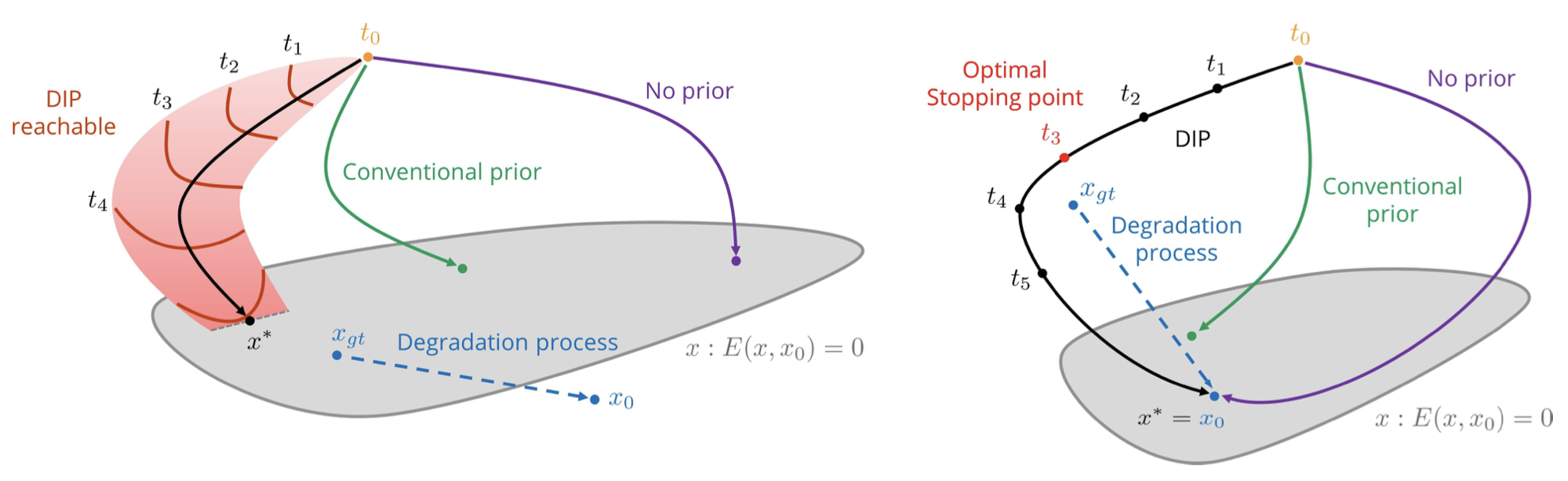
• 왼쪽 (super-resolution 예시)
  • 여기서는 손상된 image $x_0$에서 원본 image $x_{gt}$를 restoration 하려는 상황
  • 회색 영역은 energy가 0인 점들을 나타내는데, 최적화가 이 공간에 도달하면 원본과 동일한 image가 나오는 것이 목표
  • "No prior" (보라색 경로): priors 없이 최적화를 하면, solution $x^*$가 원본 image $x_{gt}$에서 멀리 떨어진 지점에 도달할 수 있음. 최적화 경로가 제대로 조정되지 않기 때문에 좋은 결과를 얻기 어려움
  • "Conventional prior" (녹색 경로): 전통적인 priors를 추가하면, 최적화가 더 효율적으로 진행되어 원본 image에 더 가까운 지점에 도달하게 됨
  • "DIP (Deep Image Prior)" (빨간 경로): deep image prior을 사용하면, network 구조 자체로 최적화를 유도해 더 나은 결과를 낼 수 있음. 이는 $t_3$ 시점에서 좋은 결과를 얻게 해줌
• 오른쪽 (denoising 예시)
  • 여기서는 손상된 image $x_0$에서 noise를 제거하려는 상황. 이 경우 원본 image $x_{gt}$와 energy가 0이 아닌 경우(손상된 정보가 있음)를 다룸
  • "No prior" (보라색 경로): Priors 없이 최적화를 하면, 너무 멀리 떨어진 나쁜 결과로 수렴할 수 있음
  • "Conventional prior" (녹색 경로): 전통적인 priors는 최적화 경로를 더 나은 방향으로 조정해 원본에 가까운 image를 생성할 수 있음
  • "DIP" (검은 경로): Deep image prior을 적용하면, 최적화 경로가 자연스러운 image를 생성하는 방향으로 유도. 이 경우 "Optimal Stopping Point"에서 최적화를 멈추면 좋은 restoration 결과를 얻을 수 있음. 너무 오래 반복하면 원본에서 멀어질 수 있으니 적절한 시점에서 멈추는 것이 중요
• 위 두 경우를 요약하면,
  • Priors는 최적화가 더 자연스러운 image에 도달할 수 있도록 돕는 중요한 역할을 함
  • Deep Image Prior (DIP)는 network 구조 자체가 priors 역할을 하며, 데이터를 학습하지 않아도 좋은 restoration 결과를 얻을 수 있음

Optimization Process

• 본 연구에서는 무작위로 초기화된 network parameter $\theta$를 gradient descent를 사용해 최적화하여 손상된 image를 restoration
• 이 방식에서 restoration을 위한 유일한 정보는 손상된 image $x_0$와 network의 구조

Network Architecture

• Network architecture는 결과에 중요한 영향을 미치며, 본 논문에서는 skip connection이 포함된 U-Net과 유사한 "hourglass" 구조를 사용
• 이 구조는 image restoration에 효과적이며, 실험에서 학습된 데이터 없이도 성능이 우수

Optimization of Code $z$

• 본 연구의 실험에서는 code $z$를 최적화하지 않고, 대신 network 구조만을 사용해 image restoration 문제를 해결

2.1. A Parametrization with High Noise Impedance

Key Question

• High capacity network $f_\theta$가 모든 가능한 image, 심지어는 random noise까지도 재현할 수 있으므로, network가 생성된 image에 제한을 가하지 않는다고 생각할 수 있음

The Impact of Network Architecture

• 하지만 network 구조가 gradient descent와 같은 방법이 솔루션 공간을 탐색하는 방식에 중요한 영향을 미침
• 특히, network는 'bad solution(좋지 않은 해)'를 저항하며 자연스러운 image에 더 빠르게 수렴

Optimization results

• 식 (2)를 minimization 하는 과정에서 network는 자연스러운 local optimum에 도달하거나, 최소한 그 근처를 통과

Basic reconstruction problem

• 주어진 target image $x_0$를 재현할 수 있는 parameter $\theta^*$를 찾는 문제를 정의할 수 있음
• 이를 위해 다음과 같은 L2 distance data term을 사용:

  $E(x; x_0) = \|x - x_0\|^2$

• 이 수식을 식 (2)에 대입하면, 다음과 같은 최적화 문제로 변환:

  $\min_\theta \|f_\theta(z) - x_0\|^2$

Experiment Results

• 아래 그림에서는 네 가지 image $x_0$에 대해 gradient descent iteration에 따른 energy $E(x; x_0)$의 변화를 보여줌

  

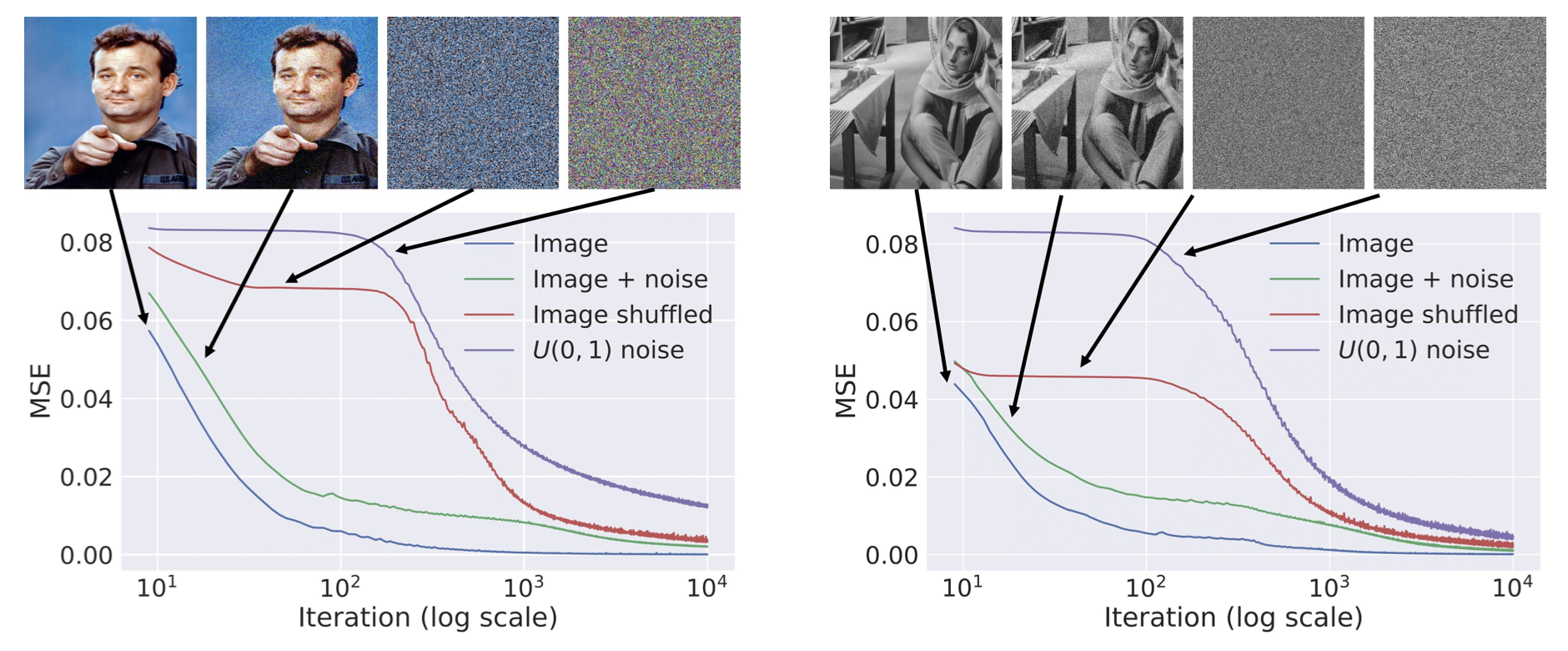
• 항목은 아래와 같이 구성
  1) Natural image
  2) Noise가 추가된 natural image
  3) Pixel이 random하게 섞인 image
  4) White noise

• Natural image(1, 2)의 경우 최적화가 훨씬 빠르게 진행되며, random pixel이나 noise(3, 4)의 경우에는 network가 높은 "관성"을 보임

• 이는 network가 신호에 대해 낮은 저항성을 보이고, noise에 대해서는 높은 저항성을 제공함을 의미

Application

• 일부 application에서, 최적화 iteration을 제한하여 deep image prior을 적용
• 이는 parameter $\theta$가 random initialization $\theta_0$에서 크게 벗어나지 않은 상태에서 생성할 수 있는 image의 제한된 집합에 투영하는 효과를 가짐

2.2 "Sampling" from the Deep Image Prior

Prior Sampling

• 식 (2)로 정의된 prior은 명시적인 확률 분포를 정의하지 않지만, parameter $\theta$의 random 값으로부터 image를 생성함으로써 샘플을 추출할 수 있음
• 최적화가 시작되기 전에 network가 생성할 수 있는 image의 출발점을 시각화할 수 있음

Visualization Results

• 그림 5는 다양한 hourglass-type(모래시계형) architecture에서 deep prior을 통해 생성된 샘플들을 보여줌
• 이 샘플들은 공간 구조와 자기 유사성을 보이며, 구조의 scale은 network의 depth에 따라 달라짐

Effect of Skip Connections

• Skip connection을 추가하면 다양한 특성 scale을 포함하는 image가 생성되며, 이는 natural image를 모델링하는 데 적합
• 이러한 이유로 이러한 architecture가 generative ConvNets에서 가장 널리 사용

Image Restoration Performance

• Image restoration 실험에서도 이러한 architecture가 가장 우수한 성능을 보임

---

3. Applications

3.1. Denoising and Generic Reconstruction

Noise Filtering

• 본 연구의 parameterization은 noise에 대한 높은 저항성을 가지기 때문에 자연스럽게 image를 restoration 하면서 noise를 제거하는 데 사용할 수 있음

Objective

• Noise가 섞인 image $x_0$에서 깨끗한 image $x$를 restoration하는 것
• 때로는 noise 모델 $x_0 = x + ϵ$이 알려져 있지만, 대부분의 경우 noise 모델은 알 수 없으며, 이 경우를 blind denoising이라고 함

Method

• 이 논문에서는 noise 모델을 알 수 없는 blind denoising 상황을 다루지만, noise 모델에 대한 정보를 사용할 수 있도록 쉽게 수정할 수 있음
• 수식 (3)과 (4)를 사용하여 손상된 image $x_0$로부터 깨끗한 image를 restoration

Advantages

• Image 손상 과정에 대한 모델을 필요로 하지 않으며, 복잡하고 알려지지 않은 압축 artifact가 있는 image restoration 작업에도 적용할 수 있음
• 이 방법은 supervised learning을 위한 현실적인 데이터를 얻기 어려운 경우에도 사용 가능

Experiment Results

• 표준 데이터셋에서 9개의 color image에 대해 noise 강도 $\sigma = 25$로 테스트했으며, 1800번의 최적화 후 PSNR 29.22를 달성
• 마지막 반복에서 restoration 된 image를 평균화하면 PSNR이 30.43까지 증가하고, 최적화 과정을 두 번 반복하면 PSNR 31.00까지 개선

Comparison

• 아래 그림은 CMB3D와 Non-local means 같은 사전 학습이 필요 없는 방법들과 비교했을 때, 본 논문의 방법은 더 나은 성능을 보임

Blind Restoration Process of a JPEG-Compressed Image

• 아래 그림은 JPEG compression으로 손상된 image의 restoration 과정을 보여주고 있음

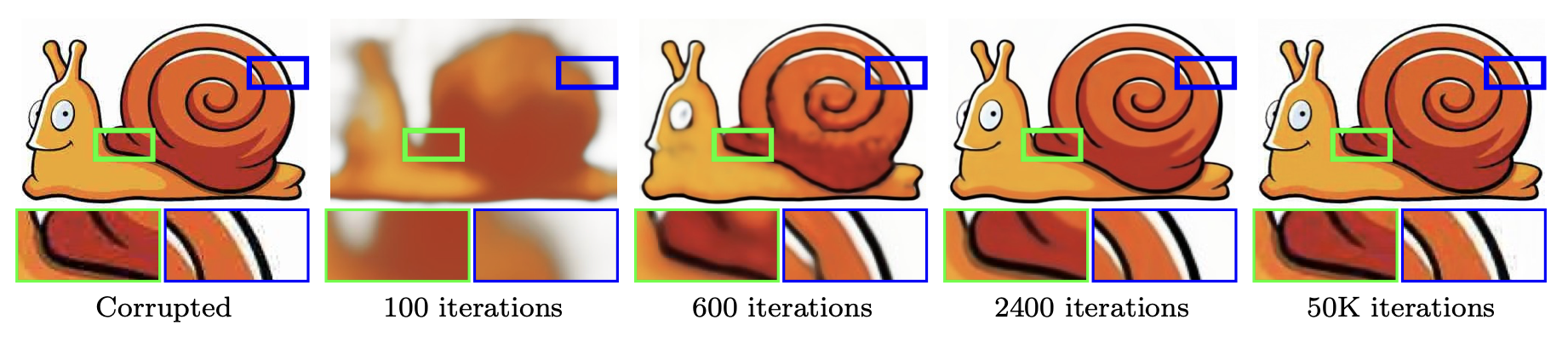
• Corrupted (손상된 image): 처음 image가 압축되면서 할로(halo)나 블록 noise(blockiness) 같은 artifact가 포함된 상태를 보여줌
• 100 iterations (100회 반복): 100번의 최적화가 진행된 후, image는 아직 흐릿하고 선명하지 않지만, 일부 구조가 조금씩 restoration 되는 단계
• 600 iterations (600회 반복): 이 단계에서는 더 많은 디테일이 restoration 되었으며, 윤곽이 점점 선명해지고 있음. 할로와 블록 noise가 많이 사라진 상태
• 2400 iterations (2400회 반복): 대부분의 신호가 restoration되었고, 할로와 블록 noise도 거의 제거. 이 시점에서는 대부분의 중요한 정보가 잘 restoration 된 상태
• 50K iterations (50,000회 반복): 너무 많은 반복을 하게 되면, 최적화가 원본에 overfitting 되면서 원하지 않는 패턴이 추가되거나 품질이 떨어질 수 있음. 이 단계에서는 약간의 품질 저하가 다시 나타나기 시작
• Summary
  • Deep Image Prior는 압축과 같은 복잡한 손상을 restoration할 수 있음
  • 적절한 반복 횟수에서 최적화를 멈추는 것이 중요하며, 2400회에서 최적의 결과를 얻을 수 있음
  • 50,000회 반복과 같이 최적화를 지나치게 많이 하면 overfitting이 발생할 수 있음

Conclusion

• Network architecture가 매우 중요한 영향을 미치며, architecture에 따라 매우 다른 성능을 보임
• 예를 들어, UNet은 fitting이 너무 빨리 진행되는 반면, ResNet은 fitting이 너무 느리게 진행됨

3.2. Super-resolution

Objective

• 저해상도(LR) image $x_0$를 입력으로 받아 고해상도(HR) image $x$를 생성하는 것
• 주어진 저해상도 image가 고해상도 image로 축소될 때 동일한 저해상도 image를 만들어야 함

Equation

• 수식 (5)에서 데이터 항은 다음과 같이 정의:

  $E(x; x_0) = \|d(x) - x_0\|^2$

• 여기서 $d(x)$는 고해상도 image를 저해상도로 축소하는 연산자이며, 최적화 문제는 축소된 image가 입력 저해상도 image와 동일한 HR image를 찾는 것임

Problem

• 이 문제는 잘 정의되지 않은 문제(ill-posed problem)로, 무한히 많은 HR image가 동일한 LR image로 축소될 수 있기 때문에, 이 중에서 가장 적절한 해를 선택하기 위해 정칙화가 필요

Method

• Deep image prior을 사용하여 reparameterization $x = f_\theta(z)$를 통해 문제를 정칙화하고, 이를 gradient descent로 최적화

Experiment Results

• Set5와 Set14 데이터셋을 사용하여 super resolution 성능을 평가
• 본 논문의 방법은 학습 기반 방법들에 비해 PSNR 성능이 다소 낮지만, 학습되지 않은 방법들(bicubic 등)보다는 훨씬 나은 성능을 보임

Visualization Results

• Bicubic upsampling 및 최신 학습 기반 방법들과 비교

• 본 논문의 방법은 학습 없이도 시각적으로 우수한 결과를 도출했으며, 학습된 ConvNet 방법들과의 격차를 상당 부분 좁혔음

---

6. Discussion

Summary of the Study

• 본 논문에서는 최근 image generation network의 성공을 조사하면서, network architecture에 의해 형성된 prior이 학습을 통해 외부 image로부터 전달된 정보와 어떻게 구분되는지를 분석
• 특히, random으로 초기화된 ConvNet을 손상된 image에 맞추는 방식이 restoration 문제에서 다목적으로 사용할 수 있는 방법임을 보여줌
• 그러나 이 방식은 대부분의 실용적인 응용에서 너무 느리고, 특정 application에 맞춰 학습된 feed-forward network가 더 나은 성능을 더 빠르게 제공할 것

Key Limitations

• 실용적인 응용을 고려할 때, 속도 문제와 특정 문제 해결 방법의 성능을 능가하거나 맞추지 못한다는 것이 이 접근법의 주요 한계점임
• 그럼에도 불구하고 다양한 restoration 작업에서 좋은 결과를 보여주며, 이는 deep convolution network 구조에 내재된 prior이 image restoration 작업에서 중요한 역할을 함을 입증

Origin of the Prior

• 왜 이런 prior이 natural image의 구조에 잘 맞을까? 본 논문에서는 convolution 연산에 의한 생성이 자연스럽게 self-similarity을 강요한다고 추측
• convolution filter가 전체 시각 영역에 걸쳐 적용되면서, 출력에 일정한 stationarity를 부여
• 또한, hourglass 구조와 skip connection은 여러 scale에서 self-similarity를 자연스럽게 부여하여, natural image restoration에 적합한 prior을 제공

Difference from the Conventional Narrative

• 본 연구의 결과는 deep learning이 image restoration에서 성공하는 이유를 단순히 학습 능력으로 설명하는 기존의 서사와는 다소 상반됨
• 본 논문에서는 적절히 설계된 network architecture가 더 나은 handcrafted priors를 형성하며, ConvNets 학습은 이 기반 위에 이루어진다고 주장
• 이는 새로운 deep learning architecture를 개발하는 것의 중요성을 다시 한 번 확인시켜줌