[논문 정리] VPTQ: Extreme Low-Bit Vector Post-Training Quantization For Large Language Models

Microsoft

https://arxiv.org/abs/2409.17066

---

1. Introduction

• LLMs (Large Language Models)는 크기가 증가함에 따라 복잡한 작업에서 우수한 성능을 발휘하지만, 모델의 큰 무게는 효율적인 추론과 실제 배포에서 어려움을 야기
• 이로 인해 메모리 용량과 저장 공간에 큰 영향을 미치고, 추론 시 상당한 대역폭이 필요
• Weight-only quantization은 floating-point 숫자를 적은 bit로 표현하여 모델의 크기를 효과적으로 줄이는 방법임

Weight-only Quantization in LLMs

• Post-Training Quantization (PTQ)는 모델을 재학습하지 않고 weight를 quantization하는 방법이며, 주로 fixed-point 숫자로 변환

  https://velog.io/@bluein/research-2 블로그 정리 게시글 참고

• 최근 연구들은 3-4 bit quantization에서도 원본 모델과 유사한 정확도를 달성
• 하지만 2 bit quantization에서는 숫자 표현의 한계로 weight 표현이 제한
• BitNet은 2 bit 이하로 quantization할 수 있지만, 이를 위해 많은 GPU 자원이 필요

LLM Quantization Algorithm Comparison

• 위 표는 LLM(대형 언어 모델)에서 사용되는 다양한 quantization 알고리즘을 비교한 것으로, VPTQ, AQLM, QuIP#, GPTVQ, GPTQ, AWQ 등의 성능을 다차원에서 평가
• Effective Bitwidth:
  • 모델의 weight를 quantization할 때, 더 낮은 bit로 얼마나 효과적으로 표현할 수 있는지를 나타냄. 낮은 bit로 더 효율적인 표현이 가능할수록 모델의 압축 효율이 높아짐
  • VPTQ, AQLM, QuIP#은 이 부분에서 좋은 성능을 보여줌 (↑)
• Accuracy @ Low-bit:
  • 모델이 2-4bit로 quantization되었을 때도 여전히 높은 정확도를 유지하는지를 평가
  • VPTQ, AQLM, QuIP#은 낮은 bit에서 높은 정확도를 유지하지만, GPTVQ, GPTQ, AWQ는 성능이 떨어짐
• Quantization Time Cost:
  • Quantization 과정에서 소요되는 시간. 시간이 많이 들수록 비효율적
  • VPTQ는 적절한 수준의 시간 비용을 소모하는 반면, QuIP#은 높은 시간 비용이 요구 (↑↑)
• Inference Throughput:
  • Quantization된 모델이 추론을 실행할 때, 얼마나 많은 데이터를 빠르게 처리할 수 있는지를 평가. 추론 처리량이 높을수록 성능이 좋음
  • VPTQ와 AQLM은 추론 처리량에서 우수한 성능을 보이며, 특히 VPTQ는 추론 속도가 다른 알고리즘에 비해 빠름 (↑)

Vector Quantization (VQ)

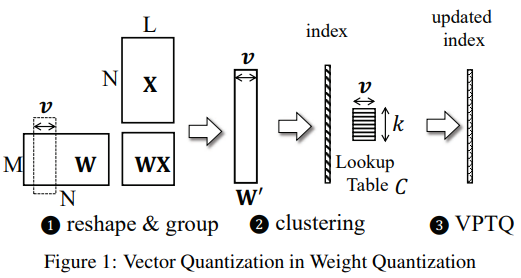
• VQ는 미리 정의된 코드북(lookup table)을 사용하여 고차원 vector를 낮은 차원의 vector로 매핑
• VQ는 고차원 데이터를 압축할 때, 데이터를 일정한 범주로 나누어 각 범주의 대표값을 저장하는 방식인데, 이때 이 대표값들을 저장하는 것이 코드북
• 이는 저장 공간을 크게 줄이면서 간단한 인덱스 참조로 원본 vector를 복원할 수 있음
• VQ는 데이터 차원 간의 상관관계를 활용하여 더 높은 압축률을 달성할 수 있음

VQ의 주요 challenges

1. 정확도 유지: VQ는 vector 단위로 quantization하므로, 동시에 여러 값을 quantization하면서 누적된 error가 발생할 수 있음
2. 효율적인 quantization 수행: VQ에서 weight matrix를 인덱스로 압축하지만, 이 인덱스는 비차분적인 정수여서 학습 중 quantization 방법을 구현하는 데 어려움이 있음
3. Dequantization overhead: VQ 모델 추론에서 dequantization이 실시간으로 수행되어야 하므로 추론 속도에 영향을 미칠 수 있음

VPTQ: Vector Post-Training Quantization

• 본 논문에서는 VPTQ라는 extremely low-bit quantization을 위한 경량화된 효율적인 방법을 제시
• VPTQ의 성과:
  1. VPTQ는 LLaMA-2/3/Mistral-7B에서 SOTA(최고 성능) 정확도를 달성
  2. VPTQ는 기존 알고리즘 대비 10.4-18.6%의 quantization 알고리즘 실행 시간만 필요
  3. VPTQ로 quantization된 모델은 SOTA 대비 1.6-1.8배 추론 속도 향상

---

2. Background and Motivation

2.1. Post Training Quantization in LLM

• Post-Training Quantization (PTQ)는 모델 재학습 없이 weight 크기를 줄이고, 정확도를 유지하는 quantization 방법

• 최적화 문제는 아래와 같이 정의:

  $\arg \min \mathbb{E}[\mathcal{L}(\mathbf{X}, \mathbf{W} + \Delta \mathbf{W}) - \mathcal{L}(\mathbf{X}, \mathbf{W})] \approx \Delta \mathbf{W}^T \cdot g(\mathbf{W}) + \frac{1}{2} \Delta \mathbf{W}^T \cdot H(\mathbf{W}) \cdot \Delta \mathbf{W}$
  • 여기서 $\mathbf{W}$는 원래 모델의 weight, $\mathbf{\hat{W}}$는 quantization된 weight이며 $\Delta \mathbf{W} = \mathbf{\hat{W}} - \mathbf{W}$는 weight quantization 오차를 나타냄
  • 최적화 목표는 quantization이 모델의 loss function $\mathcal{L}$에 미치는 영향을 최소화하는 것

• Second-Order Optimization 방법을 사용하여 이 최적화 문제를 분석함. 이를 통해 quantization에 따른 loss function을 최소화하는 방법을 도출

  • Second-Order Optimization은 최적화 기법 중 하나로, objective function의 이차 정보(Second-Order Information)를 사용하는 방법
  • 이차 정보는 헤시안(Hessian) 행렬, 즉 함수의 이차 미분으로 구성
  • 간단히 말해, 함수의 곡률을 활용하여 최적화 과정에서 더 정확한 경로를 선택하는 방식
  • 함수의 곡률을 고려하기 때문에, gradient descent와 같은 1차 최적화 방법보다 더 정확한 경로를 선택해 최적화 속도가 빨라질 수 있음

2.2. Vector Quantization in Neural Networks

• Vector Quantization (VQ)는 고차원 데이터를 저차원 공간으로 매핑하여 압축하는 효율적인 방법

• VQ의 목적은 입력 vector와 가장 가까운 중심 vector(centroid)를 찾는 것

  $\arg \min_{i \in k} \|\mathbf{v} - \mathbf{C}_i\|^2, \forall \mathbf{v} \in \mathbf{W}'$
  • 각 vector $\mathbf{v}$는 vector 공간에서 가장 가까운 중심 vector $\mathbf{C}_i$에 매핑
  • 이를 통해 데이터 왜곡을 최소화

• 최근 연구들은 VQ를 사용하여 모델의 weight matrix를 압축하는 방법을 탐구
  

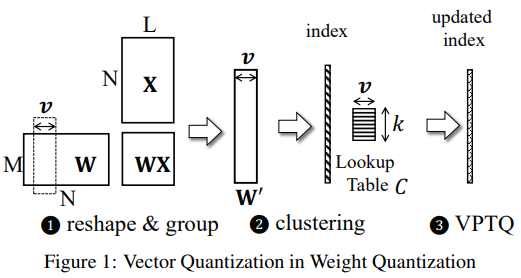
  • 예시로는 k-means 알고리즘을 사용해 vector를 그룹화하여 코드북을 만드는 과정이 있음

2.3. Vector Quantization in LLMs

• LLMs의 경우, parameter 수가 방대해 quantization 방법이 가벼우면서도 자원을 많이 소모하지 않도록 해야 함
• AQLM은 weight matrix를 quantization하면서 다중 레이어에서 학습을 동시에 수행
• GPTVQ는 Second-Order Optimization 방법을 사용하여 PTQ를 구현하지만, vector 길이가 증가할수록 quantization error가 누적되는 문제가 있음
• QuIP#는 weight matrix에 대해 무작위 Hadamard 변환을 적용하여 quantization error를 줄이지만, 이로 인해 추론 속도가 느려질 수 있음

---

3. Vector Post-Training Quantization (VPTQ)

3.1. VPTQ Algorithm

• VPTQ는 Second-Order Optimization을 사용하여 extremely low-bit quantization을 달성
  
  • 1) 입력 데이터
    • W: Quantization 하려는 모델의 weight matrix. 이 matrix의 크기는 (M \times N)
    • H: Hessian matrix로, weight quantization 시 손실을 줄이기 위해 사용
    • E: Quantization error를 추적하는 변수
  • 2) 초기화
    • E는 quantization error를 추적하기 위해 초기화
  • 3) Quantization 과정
    • 첫 번째 iteration에서 weight matrix의 열을 나누어 처리. 각 열에 대해 Residual Vector Quantization (RVQ)가 적용. RVQ는 weight vector를 점진적으로 quantization하여 error를 줄이려는 방법
    • Q(v) 함수는 vector v에 대해 quantization를 수행. 여기서, weight matrix의 열을 처리하면서 quantization된 값을 얻음
  • 4) Quantization error 업데이트
    • Quantization 과정에서 발생한 error를 E에 기록하고, 그 error를 다시 weight에 반영하여 남은 weight들을 업데이트
    • 이를 통해 error가 누적되는 것을 막고, 전체적으로 더 나은 quantization를 수행
  • 5) Residual 처리
    • 모든 quantization가 끝난 후, 남아있는 Residual error가 있으면 이를 처리하여 weight matrix를 최종적으로 업데이트
• Weight matrix W와 hessian matrix H를 사용해 최적화 문제를 해결
• VPTQ 알고리즘은 병렬로 각 열을 quantization하며, quantization된 vector는 $\hat{W}$로 표현
• 각 열은 독립적으로 quantization되며, 이를 Channel-Independent Second-Order Optimization이라 부름

Lagrangian Function을 통한 최적화

• 최적화 문제는 Lagrangian 함수 $L(\Delta W)$를 사용해 비제약(unconstrained) 최적화 문제로 변환:

  $L(\Delta W) = \Delta W^T H(W) \Delta W + \lambda \Delta W$
  • 여기서 $\lambda$는 Lagrangian 승수이며, $\Delta W$는 weight 차이를 나타냄
  • Lagrange 함수의 편미분을 통해 최적 해를 도출

Quantization 문제 변환

• Quantization error를 최소화하기 위해, $\sum \|\mathbf{v} - \mathbf{C}\|^2 / 2H_{qq}^{-1}$을 최소화하는 방식으로 변환
• 각 열을 quantization할 때마다 가장 가까운 중심 vector $\mathbf{C}$를 찾음으로써 유클리드 거리에서 최소화하는 방식과 일치

VPTQ와 GPTVQ의 차이점

• VPTQ는 GPTVQ와 달리 vector 표현을 사용해 quantization된 데이터를 원래 matrix에 가장 가까운 형태로 유지
• GPTVQ는 여러 열을 동시에 quantization하기 때문에 quantization error가 누적될 가능성이 크며, 긴 vector(8bit 이상)를 처리하는 데 제한이 있음
• VPTQ는 더 긴 vector와 더 큰 코드북을 사용할 수 있어, 정확도와 압축 비율 면에서 우수한 성능을 보임

3.2. Optimization in VPTQ

3.2.1. Hessian-Weighted Centroid Initialization

• VPTQ는 quantization 전에 코드북 내 중심을 초기화해야 하며, 이를 통해 quantization error를 줄이고 모델 정확도를 향상

• 일반적으로 K-means clustering을 사용하여 weight matrix를 중심으로 초기화하지만, 이는 최적화 문제를 고려하지 않음

• 최적화 대상은 matrix의 추적과 Hadamard product를 이용해 다음과 같이 정의:

  $\Delta W^T \Delta W \odot H = \sum_{i=0}^{n-1} h_{i,i} \|\Delta W_{:,i}\|^2 + \sum_{i=0}^{n-1} \sum_{j=0, j\neq i}^{n-1} h_{i,j} (\Delta W_{:,i} \Delta W_{:,j})$
  • 첫 번째 항은 주요 대각 성분을 나타내며, 이는 quantization error에 가장 큰 영향을 미침
  • 두 번째 항은 weight quantization 시 다른 값과의 상호작용을 나타냄

• Hessian matrix이 주로 대각 성분으로 이루어져 있으므로, Weighted K-means 문제로 변환해 중심 초기화를 최적화할 수 있음

3.2.2. Residual Vector Quantization (RVQ)

• Residual Vector Quantization (RVQ)는 weight matrix의 quantization을 여러 단계로 나누어 처리

• 각 단계는 이전 quantization 단계에서 남은 residual error를 압축:

  $Q(v_{res}) = \arg \min_i \|v_{res} - Q(v)\| - c_i^{res}$
  • 이를 통해 압축 효율성을 높이고, quantization error를 줄임
  • 디코딩 과정에서 VPTQ는 여러 코드북에서 중심값을 읽어들여 원래 weight matrix를 재구성

3.2.3. Outlier Elimination

• 최근 연구에 따르면, outliers(이상치)가 quantization error에 크게 영향을 미침

• VPTQ는 중심 초기화 시 Hessian matrix의 대각 성분을 사용하여 이상치가 quantization에 미치는 영향을 줄임:

  $Q(v_{outlier}) = \arg \min_i \|v_{outlier} - C_i^{outlier}\|^2$
  • 이상치에 가장 영향을 받는 타일을 별도의 코드북으로 quantization하여 모델 정확도와 quantization overhead를 균형 있게 맞춤

---

4. End to End Quantization Algorithm

• End-to-end quantization algorithm은 각 레이어의 quantization만 처리하여 병렬 처리가 가능
• 각 레이어에서 Linear Operator의 weight를 quantization하며, 이상치(outlier)가 존재하면 이를 먼저 처리한 후 나머지 weight를 quantization
• Residual Quantization이 활성화되면 residual centroid 값을 사용해 weight error를 수정
• 마지막으로 레이어별로 fine-tuning을 수행하며, loss function으로 MSE를 사용
• 모든 연산이 완료된 후에는 Indexed and Codebook (C)으로 quantization된 모델을 출력

---

5. Experiments and Evaluations

5.1. Settings

• 실험은 weight-only quantization에 중점을 두고 진행
• VPTQ는 LLaMA-2, LLaMA-3, Mistral 모델에서 실험되었으며, WikiText-2, C4 등의 데이터셋을 사용
• GPTQ, GPTVQ, DB-LLM, QuIP#, AQLM과 비교하여 성능을 측정했으며, 공정한 비교를 위해 bit 너비를 동일하게 설정

5.2. Accuracy Evaluation

• LLaMA-2 모델에서 VPTQ는 QuIP#, AQLM을 2-bit quantization에서 능가하며, WikiText-2에서 perplexity가 0.5 감소

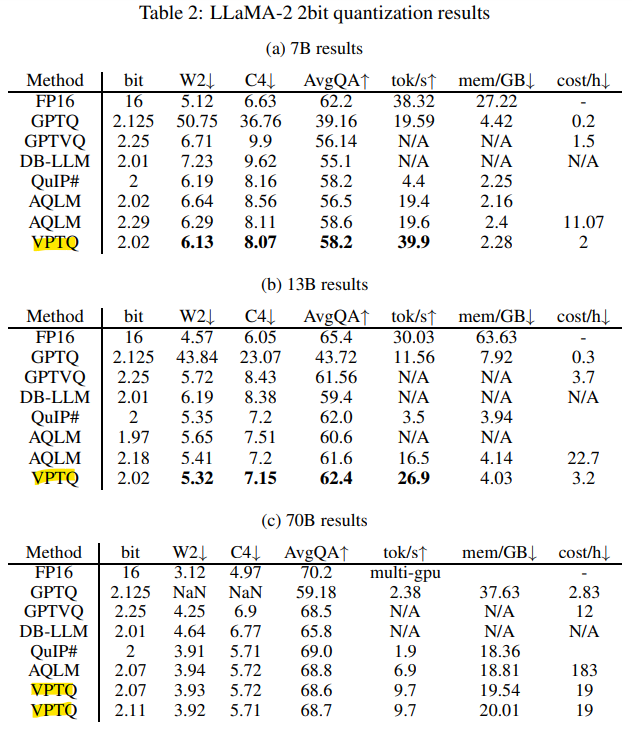
• QA 작업에서도 VPTQ가 AQLM보다 약 1% 더 나은 성능을 보임

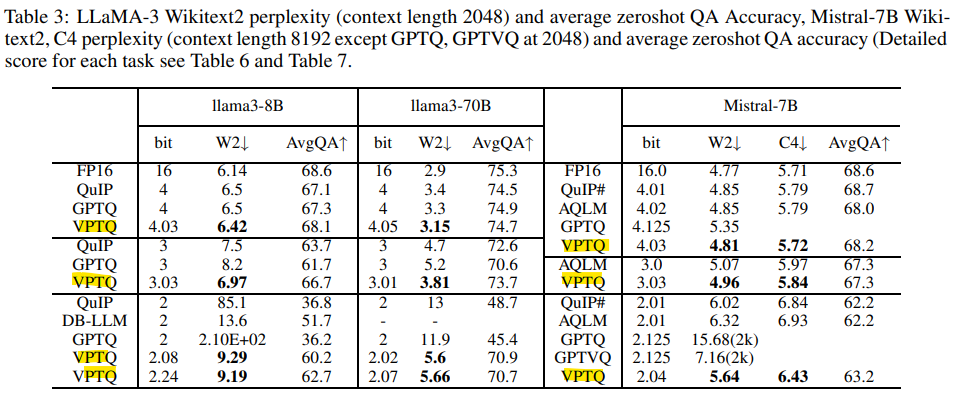
• LLaMA-3 및 Mistral 모델에서 VPTQ는 2-, 3-, 4-bit quantization에서 다른 방법들보다 우수한 성능을 보이며, 70B 모델에서 5% 미만의 정확도 손실을 기록
• 추론 속도에서는 QuIP#보다 2.2배 빠르며, AQLM보다 적은 코드북 크기를 사용해 10.4-18.6%의 실행 시간만 소요

---

6. Conclusion

• VPTQ는 Second-Order Optimization을 통해 LLMs에서 extremely low-bit quantization을 달성하는 새로운 접근법
• Residual 및 Outlier Quantization을 추가하여 모델 정확도를 높이고 크기를 줄임
• 실험 결과, VPTQ는 10.4-18.6%의 시간만을 사용하면서도 SOTA 대비 1.6-1.8배의 추론 성능 향상을 보임

---

7. Limitations

• GPU 자원의 한계로 인해 더 큰 모델(70B)에 대해 충분한 실험을 수행하지 못했음
• LLaMA-3 모델의 최신성 때문에 다른 연구와의 비교 기준이 부족함