[논문 정리] TURTLE: Let Go of Your Labels with Unsupervised Transfer

https://arxiv.org/abs/2406.07236

---

1. Introduction

Transfer learning

• Machine learning에서 중요한 개념 중 하나로, large scale pre-trained network를 이용해 제한된 자원을 가진 downstream task에서 모델 성능을 향상시키는 방법

기존 접근법

• 전체 모델을 fine-tuning하여 특정 downstream task를 해결
• 최근 연구에서는 linear probe라고 불리는 방식이 제안되었으며, 이는 pre-trained backbone을 고정한 상태에서 그 위에 linear classifier를 학습하는 방식

Foundation models

• 최근에는 foundation models가 등장하면서 다양한 task에서 human level의 성능을 보이고 있음
• 예를 들어 CLIP(Radford et al., 2021)은 이미지와 그에 해당하는 caption을 일치시키는 방식으로 pre-training을 진행하고, pre-training 후 zero-shot classifier를 만들어 data를 설명하는 시각적 카테고리의 설명을 embedding

Zero-shot transfer

• 이러한 방식이 다른 domain에서도 성공적으로 적용되고 있지만, 새로운 task를 해결하기 위해서는 여전히 human의 지시가 필요
• 여기서 중요한 질문은 foundation models의 representation을 완전히 unsupervised 방식으로 활용할 수 있는지에 대한 것

Unsupervised learning

• 기존 unsupervised learning 방식으로는 pre-trained representation에 clustering을 적용하는 방법이 있지만, 성능 저하가 나타남
• Gadetsky & Brbić (2023)의 HUME framework는 unsupervised 학습의 성능을 향상시켰지만, 여전히 task별 representation 학습이 필요

TURTLE 제안

• 이를 해결하기 위해 TURTLE을 제안
• TURTLE의 핵심 아이디어는 여러 foundation models의 space에서 linear classifier의 margin을 극대화하는 labeling을 찾아냄으로써 human labeling을 추론하는 것

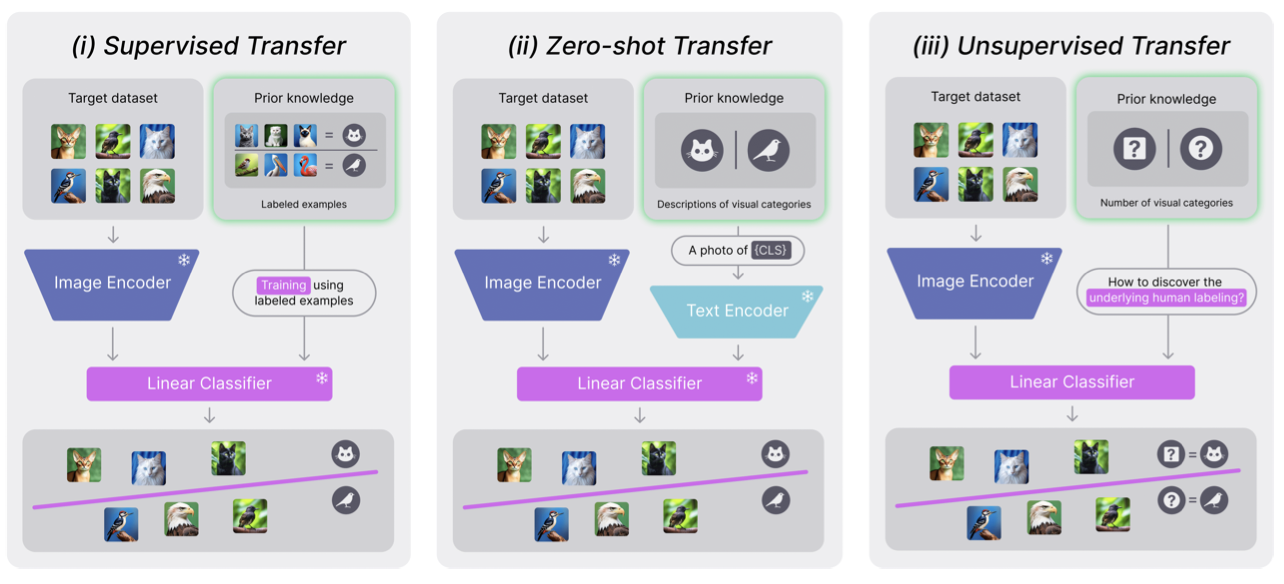
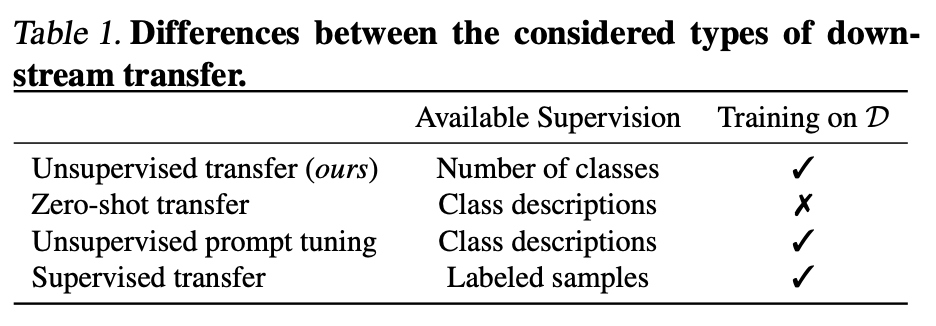
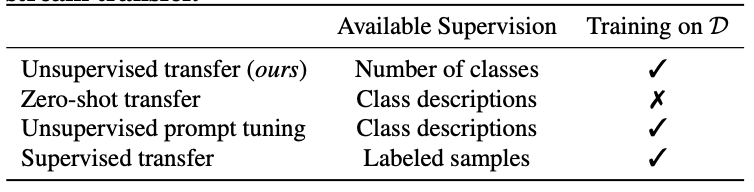
• TURTLE은 unsupervised transfer learning 방식으로, zero-shot 및 supervision transfer learning과 달리 어떤 형태의 supervision도 필요하지 않음

TURTLE 성능 평가

• TURTLE은 26개의 dataset과 7개의 foundation models에 대해 평가
• TURTLE은 state-of-the-art unsupervised 성능을 기록했으며, CLIP zero-shot transfer보다 우수한 성과를 보임
• 특히, 동일한 모델 크기와 representation space를 사용할 경우, TURTLE은 26개의 dataset 중 13개에서 CLIP zero-shot을 능가
• 또한 linear probe와 비교했을 때, TURTLE은 26개의 dataset 중 5개에서 유사한 성능을 보여, 고품질의 representation이 주어지면 label 없이도 human labeling을 추론할 수 있음을 시사

---

2. Background

Unsupervised transfer

• $X \subseteq \mathbb{R}^d$는 input space, $D = \{x_n\}_{n=1}^N$, $x_n \in X$은 N개의 샘플과 $C$개의 클래스가 포함된 dataset을 의미
• $\phi(x) : X \rightarrow \mathbb{R}^q$는 input space $X$에서 pre-trained foundation model의 $q$ 차원 representation space으로 매핑하는 function
• 이 연구는 foundation model의 representation을 사용하여 새로운 task를 unsupervised 방식으로 해결하는 방법을 찾는 것이 목적
• unsupervised transfer learning에서는 dataset $D$에 대해 human의 labeling을 supervision 없이 추론하는 것을 목표로 함

Generalization-based learning of human labelings

• Gadetsky & Brbić (2023)은 pre-trained 모델의 representation 위에 linear models를 사용해 generalization 성능을 평가하는 목표를 제시
• 이 목표는 foundation models의 representation space에서 linear models의 강력한 일반화 능력에 기반하여, 주어진 dataset에 대해 최적의 labeling을 찾아내는 것
• Labeling의 품질은 linear model이 주어진 labeling에 대해 일반화할 수 있는 능력으로 측정

Optimization problem 정의

• 위 수식에서 $\tau$는 dataset $D$의 가능한 모든 labeling에 대해 최소화되는 labeling function
• 하지만 이는 discrete optimization problem으로 이어져 매우 어려운 problem

Continuous optimization

• 이를 해결하기 위해, Gadetsky & Brbić (2023)은 discrete labeling $\tau$ 대신 task encoder $\tau_{\theta}(x) : X \rightarrow \Delta^{C-1}$로 continuous parameters $\theta$를 사용해 optimization를 진행
• 여기서 $\Delta^{C-1}$는 $(C-1)$ 차원의 probability simplex를 의미

HUME framework

• HUME은 unsupervised learning framework로, 아래 수식과 같이 모델링
  $\tau_{\theta}^{HUME}(x) = \sigma(\theta^T \psi(x)) \quad (2)$
• 수식 (2)에 대한 이해
  • $\tau_{\theta}^{HUME}(x)$: 이 값은 data point $x$가 어떤 클래스에 속할 가능성을 나타냄. 이는 task encoder가 계산한 값
  • $\theta$: 학습해야 하는 weight vector로, model이 data를 분류할 때 사용되는 중요한 parameter
  • $\psi(x)$: Input data $x$를 representation space로 변환한 값. 이 값은 self-supervised learning을 통해 pre-trained model이 data의 feature를 추출한 결과
  • $\sigma(\cdot)$: Softmax 또는 Sigmoid 같은 activation function. 이는 계산된 결과를 0과 1 사이의 확률 값으로 변환. 이 값이 각 클래스에 속할 확률을 나타냄
• 요약하자면, input data를 pre-trained moedl을 통해 feature vector로 변환한 후, linear model과 activation function을 사용해 각 data가 어떤 클래스에 속할 확률을 계산하는 과정을 나타냅
• 그러나 이 방법은 특정 task별 representation 학습이 필요하므로 large scale data가 필요하며, data가 제한된 경우 unsupervised transfer learning이 어려워짐

HUME optimization objective function

• 여기서 $\mathcal{L}_{ce}$는 cross-entropy loss function이고, $f_{approx}$는 iterative optimization 알고리즘을 사용해 구한 $\hat{f}$의 근사 해
• HUME은 iterative differentiation을 사용해 이중 optimization problem(bilevel optimization problem)를 해결

---

3. Analysis of Generalization-Based Objective

Binary labeling의 경우

• Generalization-based objective를 분석하기 위해, 이 절에서는 $\tau(x) : X \rightarrow \{-1, +1\}$인 binary labeling과 exponential loss function인 $\mathcal{L}_{exp}(f(x), \tau(x)) = \exp(-\tau(x)f(x))$을 고려
• 분석을 단순화하기 위해 task encoder $\tau_{\theta}$가 동일한 representation space $\phi(x)$에서의 linear model이라고 가정
• 즉, $\tau_{\theta}(x) = \sigma(\theta^T\phi(x))$이며, 여기서 $\sigma$는 $\text{tanh}$ 같은 activation function
• 이 가정은 representation space에서 선형적으로 구분 가능한 labeling 집합으로 search space를 제한하는 것과 같음

optimization 과정

• $w_{M} = \Xi^{(M)}(w_0, D)$는 $w_0$에서 시작하는 optimization 알고리즘의 $M$단계 후 결과를 나타냄
• $w_{m+1} = \Xi(w_m, D)$는 gradient descent로 representation되며, 단계 크기 $\eta$를 사용

Bilevel optimization problem 정의

• 이 수식은 inner objective와 outer objective로 나뉨

Main result

• 이 분석의 중요한 관찰은 inner optimization이 선형적으로 구분 가능한 data에서 logistic regression의 해와 관련이 있다는 점
• Gradient descent는 max-margin hyperplane 방향으로 수렴하게 됨
• 주어진 labeling $\tau_{\theta}$에 대해 $w_M$는 max-margin hyperplane 방향을 따름
• 따라서, optimization이 진행될수록 max-margin classifier를 유도하는 labeling을 얻게 됨

Proposition 3.1

• 여기서 $g(\theta) = (M\eta\exp(\|r_M(\theta)\|^2))^{-1}$이며, $r_M(\theta)$는 남은 값(residual)으로 $\lim_{M \to \infty} \|r_M(\theta)\|^2 = 0$이 성립
• $w_{SVM}(\theta)$는 주어진 $\theta$에 대한 hard-margin SVM의 해:
  $w_{SVM}(\theta) = \min_w \|w\|^2_2$
  $\text{s.t.} \quad \tau_{\theta}(x_n)w^T\phi(x_n) \geq 1 \quad \forall x_n \in D \quad (7)$
• 이 결과는 hard-margin SVM에 대한 해의 norm이 generalization-based objective를 통해 upper bound 됨을 보여줌
• Proposition 3.1에 대한 이해
  • Gradient descent가 max-margin을 찾도록 유도하여, 클래스 간의 거리를 최대화하는 선을 그린다는 결과를 보여줌
  • 이는 SVM에서 두 클래스를 가장 잘 구분하는 선을 찾고, 그 선과 가장 가까운 data 사이의 거리를 최대화하는 방식과 유사
  • TURTLE framework는 이 원칙을 여러 foundation models에 적용하여 최적의 labeling을 찾음

---

4. TURTLE Framework

Optimization objective

• Proposition 3.1에서 도출한 inductive bias를 기반으로, 본 논문에서는 TURTLE이라는 framework을 제안
• 이는 여러 foundation models의 representation space에서 동시에 linear models의 margin을 최대화하여 labeling을 찾는 방식
• $K$개의 foundation models가 주어졌을 때, $ϕ_k(x)$는 $k$번째 foundation model의 representation space를 의미
• Task encoder $τ_{\theta}$에 의해 정의된 labeling을 고려했을 때, $w_k^M$는 이 labeling을 학습하기 위해 $ϕ_k(x)$ representation space에서 학습된 $k$번째 linear model
• TURTLE의 optimization objective function은 다음과 같음:

• 수식 (8)에 대한 이해
  • $\sum_{k=1}^{K}$: 여러 개의 foundation models ($K$개)을 고려한다는 의미. 각각의 모델은 서로 다른 representation space를 제공하며, TURTLE은 이 모든 모델에서 동시에 optimization
  • $\sum_{x \in D}$: Dataset $D$에 있는 각 샘플에 대해 계산을 진행. 즉, 모든 샘플이 학습 과정에 참여
  • $w_k^M \phi_k(x)$: $k$번째 foundation model의 representation space에서 $M$단계 동안 학습된 linear model $w_k^M$이 해당 샘플 $x$를 어떻게 분류하는지 나타냄
  • $\mathcal{L}_{ce}$: 이는 cross-entropy loss로, 모델의 예측이 label $\tau_{\theta}(x)$과 얼마나 일치하는지를 측정하는 loss function
    • $\tau_{\theta}(x)$는 task encoder가 data point $x$에 대해 계산한 추정된 labeling
  • $w_k^M = \Xi^{(M)}(w_k^0, D)$: $w_k^M$은 $k$번째 모델에서 $M$단계 동안 gradient descent로 학습된 결과. $w_k^0$에서 시작해 $M$번의 업데이트 후 도달한 값
• 이 수식은 여러 foundation models에서 linear model의 margin을 동시에 최대화하면서 labeling을 찾는 과정
• 각 모델이 data를 어떻게 분류하는지를 측정하고, 그 결과를 기반으로 모든 모델에서 공통된 최적의 labeling을 찾는 것이 목표

Task encoder parametrization

• Task encoder $τ_{\theta}$의 parameter는 labeling search space를 정의하며 optimization 과정에 중요한 역할을 함
• TURTLE에서는 pre-trained foundation models의 representation space를 사용해 task encoder $τ_{\theta}$를 정의하고, 이 representation은 학습 절차 동안 고정되어 task-specific representation learning이 필요하지 않음
• 구체적으로, $K$개의 representation space $ϕ_k(x)$가 주어졌을 때 task encoder $τ_{\theta}$는 다음과 같이 정의:

• 수식 (9)에 대한 이해
  • $\tau_{\theta}^{TURTLE}(x)$는 data point $x$가 어떤 cluster에 속하는지를 결정하는 function(즉, task encoder)를 정의
  • $K$는 여러 foundation models의 수를 의미. $K$개의 모델에서 나온 결과를 모두 평균하여 최종 labeling을 결정
  • $\phi_k(x)$는 $k$번째 foundation model에서 data point $x$의 representation을 의미
  • $\theta_k^T \phi_k(x)$는 $k$번째 모델의 parameter $\theta_k$와 data $x$의 representation $\phi_k(x)$ 사이의 내적
  • 이것을 통해 모델이 해당 data를 어떻게 분류할지를 계산
  • $\sigma$는 softmax와 같은 function으로, 이 값을 0과 1 사이의 확률로 변환하여 각 data가 특정 cluster에 속할 확률을 제공
• 즉, 수식 9는 여러 모델의 결과를 모아서 각 data가 어떤 cluster에 속할 가능성을 계산하는 과정
• 여기서 $θ = \{\theta_1, \dots, \theta_K\}$는 모든 학습 가능한 parameter이며, $\sigma$는 softmax activation function
• 학습 후 cluster 할당은 다음과 같이 계산:

• 수식 (10)에 대한 이해
  • $\tau_{\theta}^{TURTLE}(x)_c$는 data $x$가 $c$번째 cluster에 속할 확률을 나타냄
  • $\arg\max$는 그 중 가장 높은 확률을 갖는 cluster를 선택하는 function
  • 즉, 수식 10은 data point $x$가 가장 높은 확률을 갖는 cluster에 속하도록 할당하는 과정
  • TURTLE은 이 과정을 통해 data를 적절한 cluster에 분류하게 됨
• 이 representation은 clustering 시 각 샘플이 $c$번째 cluster에 할당될 확률을 나타냄

Regularization

• Task encoder는 모든 샘플을 하나의 클래스에 할당하는 degenerate labeling을 생성할 수 있음
• 이러한 labeling은 모든 representation space에서 가장 큰 margin을 갖지만, 실제로는 유의미하지 않음
• 이를 방지하기 위해 task encoder의 각 항목을 다음과 같이 정규화:

• 수식 (11)에 대한 이해

  • $R(\theta)$는 regularization 항으로, 너무 단순한 labeling(예: 모든 data를 하나의 클래스에 할당하는 것)을 방지하기 위한 방법
  • $\tau_{\theta_k}$는 $k$번째 모델의 label 분포를 나타냄. 즉, 해당 모델이 data를 어떻게 여러 클래스에 나누는지를 보여줌
  • $H(\cdot)$는 entropy function으로, label 분포가 얼마나 복잡한지를 측정. entropy가 높을수록 다양한 클래스에 고르게 분포되고, 낮을수록 한 클래스에 치우쳐 있음

• 정리하자면, 수식 11은 모든 data를 한 클래스에 몰아넣는 degenerate labeling을 피하기 위해, 각 모델의 label 분포가 적절히 다양하도록 유도하는 정규화 항

• 여기서 $\tau_{\theta_k} = (|D|)^{-1} \sum_{x \in D} \tau_{\theta_k}(x) \in \Delta^{C-1}$는 $k$번째 구성 요소의 경험적 label 분포이고, $H(\cdot)$는 이산 분포의 entropy function

Final objective function

• 최종적으로 TURTLE은 다음 objective function을 optimization:

• 여기서 $\gamma = 10$은 entropy regularization 강도에 대한 기본값
• Appendix G에서 이 hyperparameter에 대한 robustness를 보여줌

Efficient optimization

• 새로운 optimization 기반 objective function은 convex한 inner part를 가지는 bilevel optimization problem

  • Bilevel optimization은 optimization problem이 두 단계로 구성된 problem
    • Outer problem: 주된 optimization problem으로, 전체적인 목표를 optimization
    • Inner problem: 이 outer problem을 풀기 전에 먼저 풀어야 하는 하위 optimization problem. 이 하위 problem의 해가 outer problem에 영향을 미침
    • 즉, bilevel optimization은 두 단계로 이루어진 optimization problem으로, 안쪽 problem을 풀고 나서 그 결과를 바탕으로 outer problem을 해결하는 방식
  • Convex(볼록)한 problem은 optimization할 때 쉽게 풀 수 있는 problem 중 하나
    • Problem의 function이 convex하다는 것은, 그 function의 그래프가 U자형처럼 생겼다는 것을 의미하며, 이런 경우 최적의 해를 찾기가 수월

• 주어진 $\tau_{\theta}$에서 $w_k^M$을 계산하는 것은 $ϕ_k$ representation space에서 $D$에 대한 labeling $\tau_{\theta}(D)$로 logistic regression problem을 해결하는 것
• Gradient-based 기술을 사용하여 $\theta$를 학습하는 것은 다음과 같은 전체 function $d/d\theta \mathcal{L}_{TURTLE}^M$을 계산하는 것을 포함:

• 수식 (13)에 대한 이해
  • $\frac{d}{d\theta} \mathcal{L}_{TURTLE}^M$: 전체 function을 의미. 이것은 parameter $\theta$가 변경될 때 TURTLE의 loss function $\mathcal{L}_{TURTLE}^M$이 어떻게 변하는지를 나타냄
  • $\frac{\partial}{\partial \theta} \mathcal{L}_{TURTLE}^M$: 첫 번째 term은 직접적으로 $\theta$가 TURTLE의 loss에 미치는 영향을 나타냄. 이는 $\theta$가 변화할 때 loss function이 어떻게 변하는지 계산하는 기본 function
  • $\sum_{k=1}^{K} \left(\frac{\partial w_k^M}{\partial \theta}\right)^T \frac{\partial}{\partial w_k^M} \mathcal{L}_{TURTLE}^M$: 두 번째 term은 $w_k^M$ (linear model의 parameter)가 $\theta$에 의해 어떻게 영향을 받는지를 반영
    • $\frac{\partial w_k^M}{\partial \theta}$: $k$번째 모델의 parameter $w_k^M$가 $\theta$에 따라 어떻게 변하는지를 나타내는 Jacobian
    • $\frac{\partial}{\partial w_k^M} \mathcal{L}_{TURTLE}^M$: $w_k^M$가 TURTLE의 loss function에 어떻게 영향을 미치는지를 나타내는 function
    • Jacobian의 역할:
      • Gradient와 비슷하지만, 다변수 function에서 모든 input에 대해 output에 미치는 영향을 한꺼번에 계산하는 방식
      • Optimization나 neural network 학습에서, input 변화에 따른 output 변화를 분석할 때 사용
• 여기서 $\frac{\partial w_k^M}{\partial \theta}$는 Jacobian으로 실제로는 계산 비용이 많이 듬
• 하지만 동일한 샘플 세트 $D$를 inner와 outer level에서 사용하면 두 번째 term을 생략할 수 있음
• $\partial \mathcal{L}_{TURTLE}^M/\partial w_k^M \approx 0$임이 증명되어 있음

---

5. Experiments

5.1. Experimental setup

Datasets and evaluation metric

• TURTLE의 성능은 26개의 vision dataset에서 평가
• TURTLE에서 찾은 labeling을 실제 label과 매칭하기 위해 Hungarian algorithm을 사용
• 기본적으로 training split에서 학습하고 test split에서 결과를 도출하였으며, 테스트 data만 사용했을 때도 성능 저하는 없었음

Foundation models in TURTLE

• TURTLE은 CLIP 기반 representation을 사용하며, ResNet과 Vision Transformer 모델을 포함
• 한 개의 CLIP space를 사용하는 경우 TURTLE 1-space, 두 개의 모델을 사용할 경우 TURTLE 2-spaces로 구분
• 두 space를 사용하는 경우 DINOv2와 함께 사용함. 모든 representation은 사전 계산된 후 학습 동안 고정

Baselines

• TURTLE은 HUME을 포함한 다양한 unsupervised 학습 기법들과 비교되며, zero-shot transfer 및 unsupervised prompt tuning 기법들과도 비교

• 또한 supervised linear probe 방법이 supervised baseline으로 사용

Model Selection

• TURTLE은 unsupervised hyperparameter search를 사용하며, supervised linear probe의 경우 cross-validation을 통해 L2-regularization strength를 search

5.2. Results

Comparison to unsupervised baselines

• TURTLE은 HUME과 K-Means clustering과 비교
• 아래 그림에서 볼 수 있듯이, TURTLE은 모든 dataset에서 HUME을 크게 능가하며, 특히 MNIST와 Birdsnap dataset에서 각각 23%와 11%의 절대 성능 향상을 보임

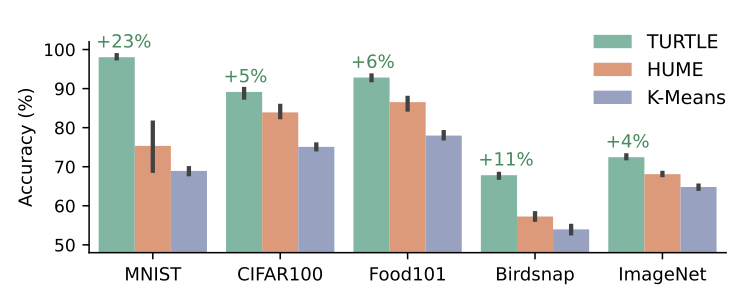
• 또한, ImageNet dataset에서 72.9%의 정확도로 이전 SOTA 성능을 5.5% 초과하며 새로운 unsupervised 학습 성능을 기록

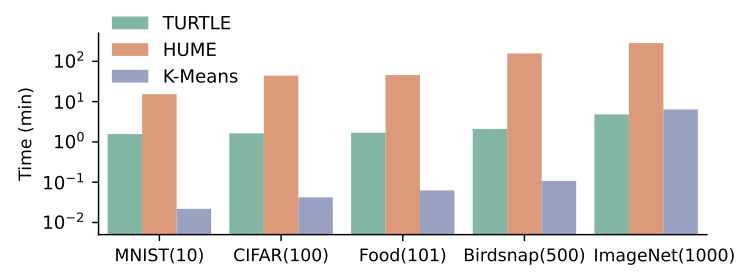
• 위 그림에서 처럼, TURTLE은 HUME 대비 10배 빠른 학습 속도를 기록하며, 특히 ImageNet dataset에서 5분 미만의 학습 시간을 보임

Comparison to zero-shot transfer

• 아래 그림과 같이, TURTLE 2-spaces는 26개 dataset에서 CLIP zero-shot transfer보다 큰 폭으로 성능이 향상

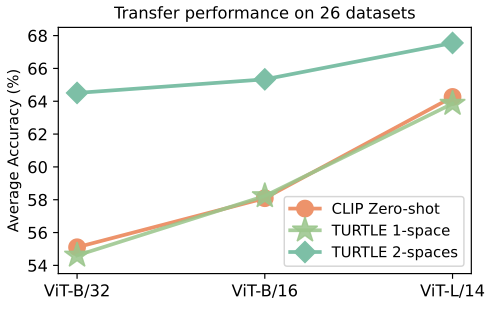
• ViT-B/32, ViT-B/16, ViT-L/14 backbone을 사용한 실험에서 각각 9%, 7%, 4%의 절대 성능 향상을 기록

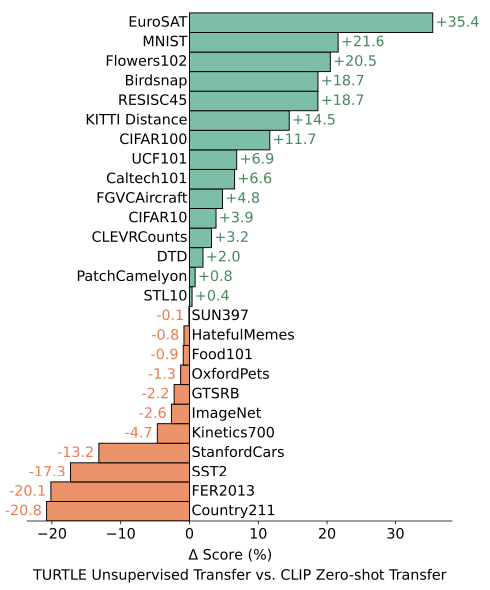
• 위 그림과 같이, TURTLE은 EuroSAT, MNIST, Flowers102 dataset에서 각각 35%, 21%, 20%의 절대 성능 향상을 보임

Comparison to unsupervised prompt tuning

• TURTLE은 unsupervised prompt tuning 기법들을 크게 앞섬

• ZS 열은 해당 방법이 zero-shot supervision을 사용하여 예측하는지를 나타냄
• 모든 방법이 CLIP ResNet-50 representation을 사용하며, TURTLE은 추가적으로 DINOv2 representation space를 두 번째 space으로 사용
• Flowers102와 EuroSAT dataset에서 각각 27%, 41%의 절대 성능 향상을 기록하며, 평균적으로 8%의 절대 향상을 달성

Comparison to supervised transfer

• TURTLE 1-space ViT-L/14와 supervised linear probe를 비교

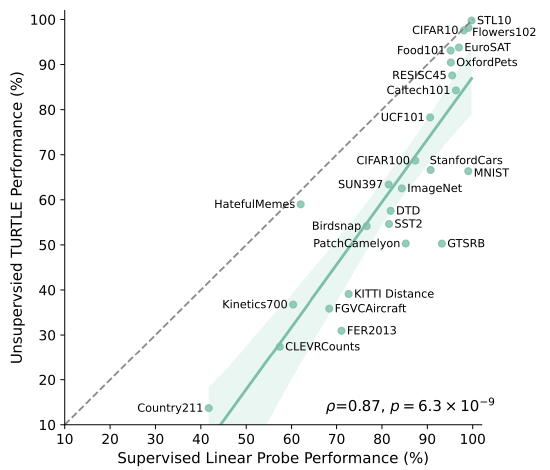
• 위 그림에서, TURTLE의 unsupervised transfer learning 성능이 supervised linear probe 성능과 높은 상관관계를 보임
  • y = x로 표시된 점선은 "optimal" unsupervised transfer learning 성능을 나타냄
  • TURTLE과 supervised linear probe 사이의 상관계수는 0.87로 매우 높음(두 가지 피어슨 상관계수의 p-value = 6.3 × 10⁻⁹)
  • TURTLE은 5개의 dataset에서 "optimal" unsupervised transfer 성능에 근접하였으며, 성능 차이는 3포인트 이하였음
• 두 모델은 동일한 representation space에서 학습되었지만, TURTLE은 supervision 없이도 높은 상관관계(0.87)를 기록
• 일부 dataset(STL10, CIFAR10 등)에서는 supervised 성능에 근접

Ablation of different representation spaces on ImageNet

• TURTLE의 성능은 더 강력한 representation space를 사용할수록 향상됨을 확인

• 상단: ImageNet-1000 dataset에서 7개의 서로 다른 representation space를 사용한 supervised linear probe 성능을 보여줌
• 하단: TURTLE의 unsupervised 학습 성능을 ImageNet-1000에서 heatmap으로 representation
• 대각선 셀은 TURTLE 1-space 성능을 나타냄
• 대각선 밖 셀은 두 개의 다른 representation space를 결합한 TURTLE 2-spaces 성능을 나타냄
• TURTLE의 unsupervised 학습 성능은 supervised linear probe 성능과 강한 양의 상관관계(상관계수 $\rho = 0.74$, p-value = 1.4 × 10⁻⁹)를 보임
• ImageNet dataset 실험에서, representation space의 품질이 높아질수록 TURTLE 성능도 향상

---

6. Related Work

(Weakly) supervised transfer

• Weakly supervision 학습은 downstream transfer를 수행하기 위해 어느 정도의 label이 필요
• 예를 들어, BigTransfer는 large scale pre-training 후 전체 모델의 fine-tuning을 통해 transfer learning을 성공적으로 수행
• 그러나 이런 방법들은 여전히 labeled data가 필요

Zero-shot transfer

• CLIP과 같은 foundation models는 human이 제공하는 설명만으로 transfer를 수행하는 zero-shot transfer를 가능하게 함
• 하지만, 이 방법도 여전히 전문가의 지식이 필요하며, TURTLE은 이러한 human guidance 없이 fully unsupervised transfer를 가능하게 함

Deep clustering

• 기존의 deep clustering 방법들은 시간이 많이 소요되는 3단계 절차를 따르며, self-supervised representation learning, clustering, self-labeling을 포함
• TURTLE은 pre-trained foundation models의 representation space를 사용하여 이러한 과정 없이 효율적으로 transfer를 수행

Maximum margin clustering

• TURTLE은 max-margin classifier의 margin을 최대화하는 labeling을 찾아내는 방법으로, 기존의 Maximum Margin Clustering (MMC)보다 더 효율적인 optimization 기법을 사용

Implicit bias of optimization algorithms

• Optimization 알고리즘의 implicit bias을 이해하는 것은 중요
• Soudry et al. (2018)의 연구는 gradient descent가 data가 분리 가능한 경우, max-margin hyperplane으로 수렴한다고 밝힘
• TURTLE은 이러한 이론을 바탕으로 unsupervised 학습을 가능하게 하는 새로운 방법을 제안

---

7. Conclusion

• 본 논문에서는 foundation models의 representation을 사용해 새로운 task를 완전히 unsupervised 방식으로 해결할 수 있음을 보여줌
• 핵심 아이디어는 maximal margin classifiers를 유도하는 labeling을 찾는 것이며, 이를 기반으로 TURTLE framework를 제안
• TURTLE은 zero-shot transfer와 비교해도 경쟁력 있는 성능을 보여주었으며, 추가적인 representation space를 사용하면 성능이 크게 향상
• TURTLE의 유연성 덕분에, 향후 더 강력한 foundation models을 활용하면 unsupervised transfer 성능이 더욱 향상될 가능성이 있음