SVM 이론

• 표기법

  편향 $\theta_0$과 입력 특성의 가중치 $\theta_1$에서 $\theta_n$까지 전체 모델 파라미터를 하나의 벡터 $\theta$에 넣는다.

  편향에 해당하는 입력값 $x_0=1$추가

  편향 = b

  특성의 가중치 벡터 = w

결정함수와 예측

$\hat{y} = \begin{cases} 0, & \mathrm{if}\ w^T x + b < 0 \\ 1, & \mathrm{if}\ w^T x + b > 0 \end{cases}$

• 결정 경계는 결정 함수의 값이 0인 점들로 이루어져 있다. → 두 평면이 교차되는 직선

• 선형 SVM 분류기를 훈련한다는 것은 가능한 한 마진을 크게하는 w와 b를 찾는 것

목적 함수

• 결정 함수의 기울기는 가중치 벡터의 norm과 같다.

  기울기를 2로 나누면 결정 함수의 값이 되는 점들이 결정 경계로 부터 2배만큼 더 멀어진다. → 마진 2배

• 가중치 벡터 w가 작을수록 마진은 커진다.

하드 마진 선형 svm 분류기의 목적 함수

$\underset {w,b} {\mathrm{minimize}} \frac {1}{2}w^Tw$

• $\lVert w\rVert$ 를 최소화하는 것 보다 $\frac {1}{2}\lVert w\rVert ^2$ 최소화 하는 것이 더 깔끔하고 간단하게 미분된다.

소프트 마진 분류기의 목적함수

• i번째 샘플이 얼마나 마진을 위반할지 정하는 슬랙변수($\zeta$)
• 하이퍼파라미터 C : 마진 오류 최소화하기 위한 슬랙변수 값을 작게 만드는 것, 마진을 크게하기 위해 $\frac {1}{2}\lVert w\rVert ^2$를 가능한 작게 만드는 트레이드오프를 정의한다.

$\underset {w,b} {\mathrm{minimize}} \frac {1}{2}w^Tw + C\sum_{i=1} ^m \zeta ^ i$

Dual problem ( 쌍대 문제 )

• primal problem이라는 제약 있는 최적화 문제가 주어지면 dual problem이란 다른 문제로 표현할 수 있다.

• Dual의 해는 Primal 해의 하한값이지만 똑같은 해가 나온다. ⇒ 둘 중 하나를 선택하여 풀 수 있다.

• Linear SVM 목적함수의 쌍대 형식

  $\underset { \alpha } {\mathrm{minimize}} \frac {1}{2}\sum_{i=1} ^m\sum_{j=1} ^m \alpha^i \alpha^j t^i t^j x^{i^T} x^j - \sum_{i=1}^m\alpha^i$

  이 식을 최소화하는 벡터 $\hat \alpha$를 찾으면 primal problem의 식을 최소화하는 $\hat w$과 $\hat b$를 구할 수 있다.

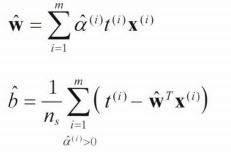
• 훈련샘플 수가 특성 개수보다 작을 때는 dual problem 푸는 것이 더 빠르다.
• primal prob.에는 커널 트릭이 적용이 안되지만 dual prob.에서는 가능하다.

커널 SVM

2차 다항식 변환 적용 후 선형 SVM 분류기를 적용

• 2차 다항식 매핑

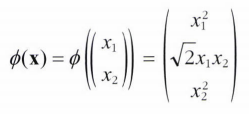
이후 벡터는 3차원이 된다.

직접 풀어서 계산해보면 알 수 있 듯이 a, b를 각각 2차 다항식 매핑식에 넣어서 dot product하면 (a.T b)의 제곱이 된다.

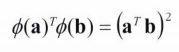
그래서 훈련 샘플을 직접 변환하지 않고 dot product 후 제곱해주면 된다.

이것이 커널 트릭이다.

• 자주 사용되는 커널

선형 :

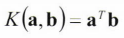
다항식:

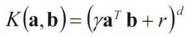
시그모이드 :

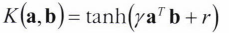
가우시안 RBF :