SVM 전반적인 설명

svm : support Vector Machine

• 고차원 데이터의 분류문제에 좋은 성능
• 트레이드오프(generalization ability, training data) 관계에서 generalization ability 증가시키는 방향
• Statistical learning theory에 근거

SVM 상황

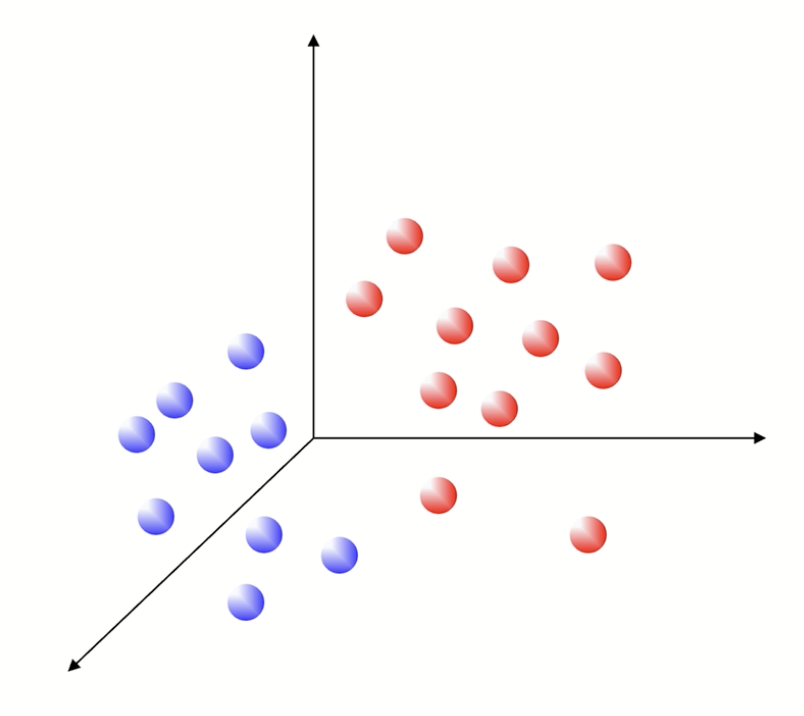
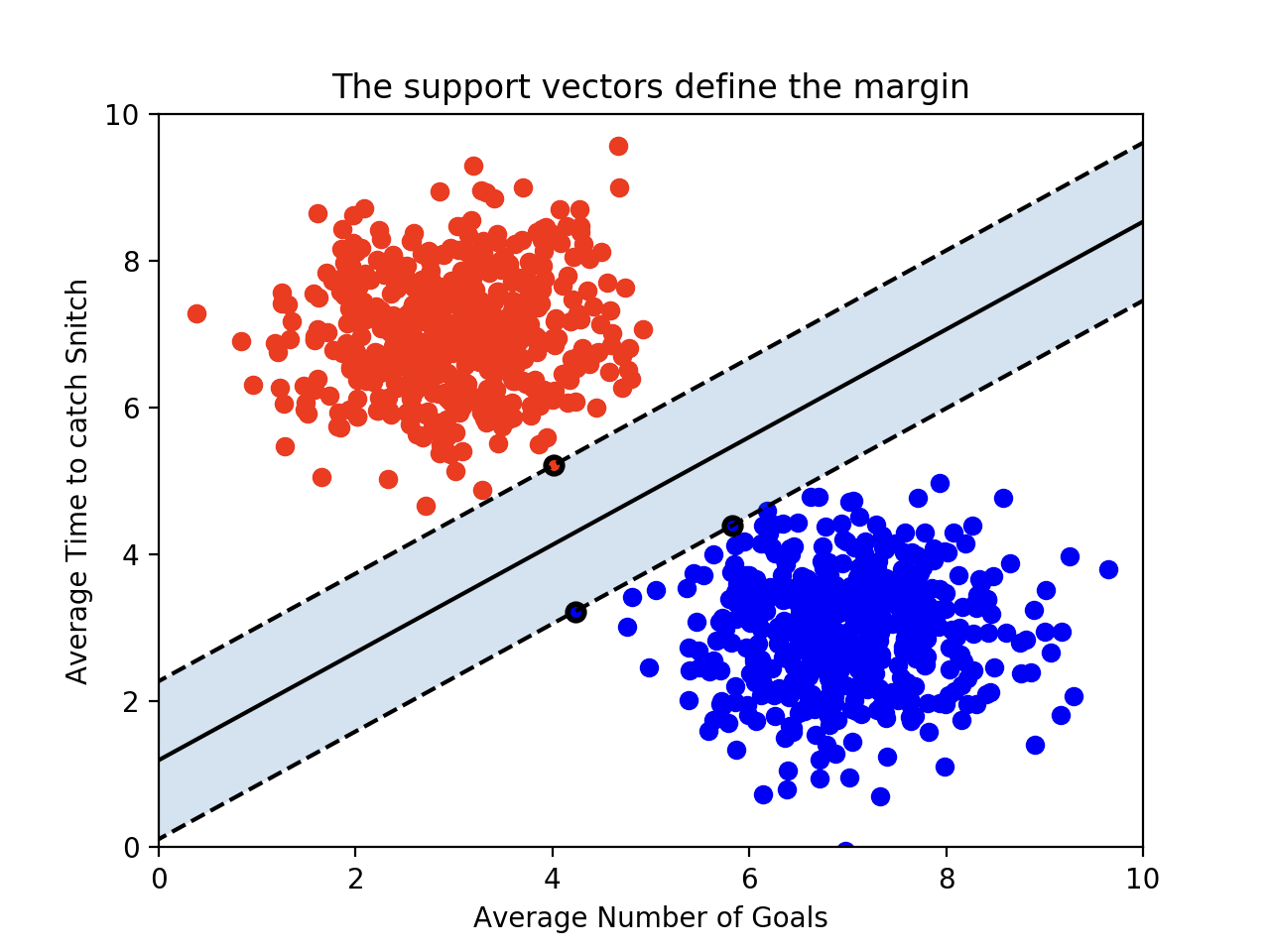
-> 이진분류문제의 예시이다.

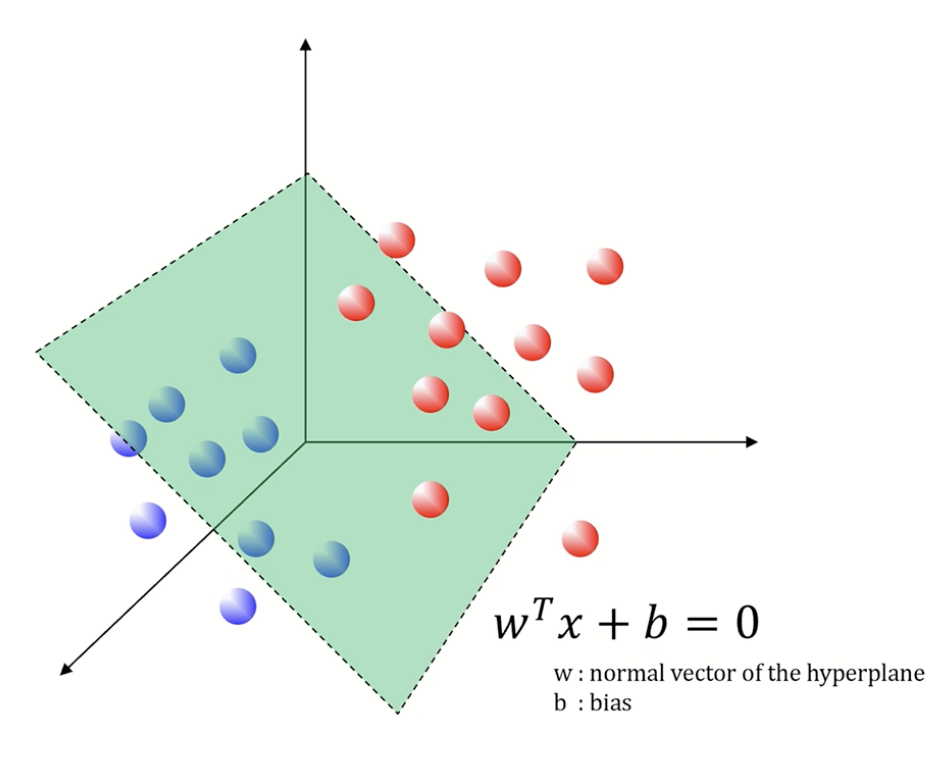
이처럼 hyper plane, decision boundary를 찾는 것이 목표이다!
그런데 이렇게 클래스를 구별할 수 있는 경계들이 너무 많다...

그러면 기준을 세워볼까...?

svm 기준 | Margin

바로 Margin!

마진을 최대화할 수 있는 hyperplane을 찾자

→ generalization error를 최소화

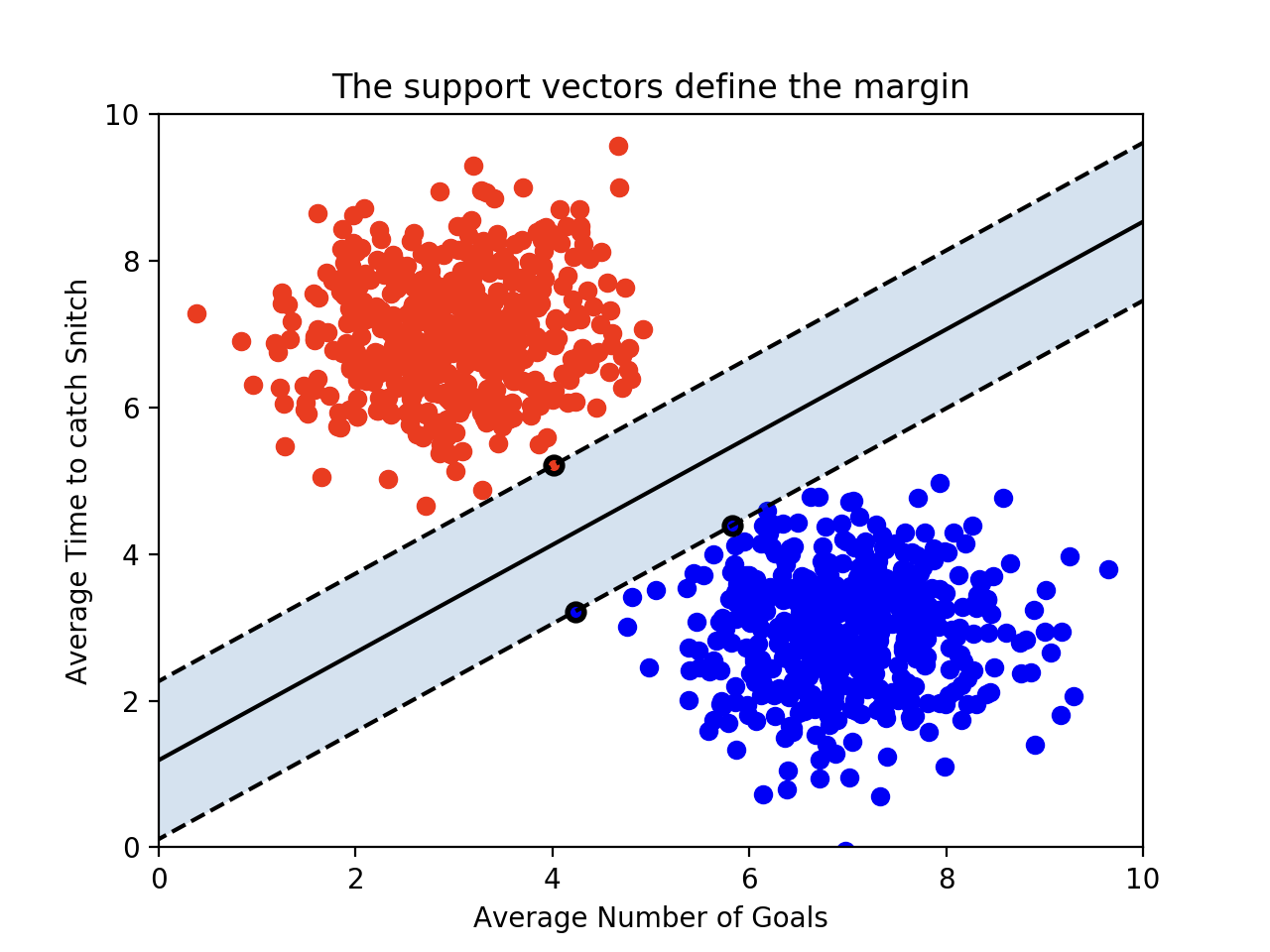
Margin : 각 클래스에서 가장 가까운 관측치 사이의 거리

W로 표현 가능 ( Wx + b )

1) Plus-plane
빨간색 클래스가 y=1

$W^TX_i + b ≥ 1$

2) Minus-plane
파란색 클래스가 y=-1

$W^TX_i + b ≤ -1$

이 2개 사이의 거리가 Margin이고 이 마진을 최대화하는 hyperplane을 찾자

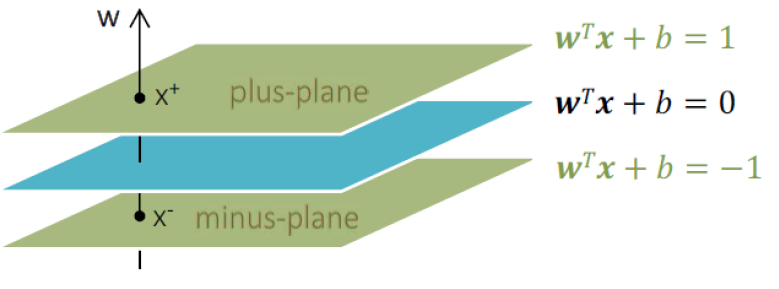
최적의 decision boundary
=> $W^TX_i + b = 0$

그리고 이 둘(+/- plane)의 관계는

$x^+ = x^- + \lambda w$

즉, 평행이동관계

수학적으로 보는 Margin

$\lambda$ 구하기

$w^Tx^++b=1$

⇒ $w^T(x^- + \lambda w)+b=1$

⇒ $w^Tx^- + b + \lambda w^Tw = 1$

여기서 $w^Tx^- + b$ = -1

⇒ $-1+\lambda w^Tw = 1$

$\lambda = \frac{2}{w^Tw}$

⚠️잊지말자 우리는 W에 주목!⚠️

Margin 구하기

$Margin$

$= distance(x^+,x^-)$

$= ||x^+ - x^-||_2$

$= ||x^-+\lambda w - x^-||_2$

$= ||\lambda w||_2$

$= \lambda \sqrt {w^Tw}$

$= \frac {2}{\sqrt {w^Tw}}$

$= \frac {2}{||w||_2}$

결론!

max margin = max $\frac {2}{||w||_2}$ ⇒ min $\frac {||w||_2}{2}$

목적식 : $minimize \frac {||w||_2^2}{2}$

제약식 : $y_i(w^Tx_i + b) ≥ 1, i=1,2,3,...,n$

Lagrangian multiplier를 이용하여 Lagrangian Primal

$max_amin_{w,b} L(w,b,\alpha) = \frac {1}{2}||w||^2_2 - \sum_{i=1}^{n}\alpha_i(y_i(w^Tx_i + b)-1)$

우선 min문제 해결 → 미분 = 0

• W에 대한 미분 ⇒ $w = \sum_{i=1}^{n}\alpha_iy_ix_i$
• b에 대한 미분 ⇒ $\sum_{i=1}^{n}\alpha_iy_i = 0$

$\frac {1}{2}||w||^2_2 = \frac{1}{2}\sum_{i=1}^{n}\alpha_iy_i(\sum_{i=1}^{n}\alpha_iy_ix_i^Tx_i) = \frac{1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\alpha_i\alpha_jy_iy_jx_i^Tx_j$

$\sum_{i=1}^{n}\alpha_i(y_i(w^Tx_i + b)-1) = \sum_{i=1}^{n}\alpha_iy_i(w^Tx_i + b) + \sum_{i=1}^{n}\alpha_i = - \sum_{i=1}^{n}\sum_{j=1}^{n}\alpha_i\alpha_jy_iy_jx_i^Tx_j+ \sum_{i=1}^{n}\alpha_i$

* 이제 $\alpha$만 구하면 W, b 알 수 있다

이제 max문제를 해결한다. | Lagrangian dual solution

$\sum_{i=1}^{n}\alpha_i -\frac {1}{2}\sum_{i=1}^{n}\sum_{j=1}^{n}\alpha_i\alpha_jy_iy_jx_i^Tx_j$

이 문제를 풀기 위해서는 KKT conditions을 만족해야 한다.

4번을 이용해서 구해본다.

1) $\alpha_i > 0$ 일 때, 뒤에가 0

⇒ +/- plane위에 위치, 이를 support vector 라고 부른다.

2) $\alpha_i = 0$ 일 때, 뒤에가 0일 필요 없다.

W, b 구하기

목표였던 W를 구하자면

support vector일 때만 $\alpha_i^*$≥ 0 이니까

support vector만 가지고 decision boundary 구할 수 있다.

b는 support vector 값 하나 $(x_{sv}, y_{sv})$ 를 넣어봐서 구할 수 있다.

지금까지 살펴본 linearly한 SVM을 HardMargin이라고 한다.

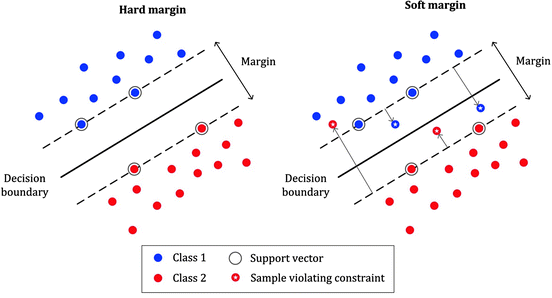
Non-linear SVM

soft margin이란

직선으로는 분류하기 힘들다

→ 약간의 error를 허용하자!

목적식 : $minimize \frac {||w||_2^2}{2} + C\sum_{i=1}^{n}\xi_i$

($\xi$ : 허용하는 error)

Hard margin과 비교해보면 뒤에 정규화 식이 붙었다.

trade-off | C

허용하는 error vs margin

C : trade-off를 결정하는 parameter

C가 높을 수록, error 많이 허용하지 않는다. ( 하드마진에 가까워진다. )

C가 작을 수록 error 많이 허용한다. ( 소프트마진에 가까워진다. )

Kernel

SVM에서 선형으로 분리할 수 없는 점들을 분류하기 위해 사용한다.

$f(x) = \sum_{i \in {SV}}\alpha_i^*y_iK + b$

• Linear Kernel
  • $K<x_1,x_2> = <x_1,x_2>$
• Polynomial Kernel
  • $K<x_1,x_2> = (a<x_1,x_2>+b)^d$
• Sigmoid Kernel
  • $K<x_1,x_2> = tanh(a<x_1,x_2> + b)$
• Gaussian Kernel (rbf kernel)
  • $K<x_1,x_2> = exp(\frac {||x_1 - x_2||_2^2}{2\sigma^2})$

출처 : [핵심 머신러닝] SVM 모델 유튜브 강의