Attention은 transformer 논문을 보면서 들었다.

이번에 포스팅으로 정리하면서 왜 attention이라고 부르는 지 궁금했는다.
RNN기반의 모델에 비해 각 단어들의 hidden vector들과 연산을 통해 무엇을 선별적으로 선택할 지를 말해주는 vector를 만들어서 무엇을 attention할 지를 말해주기 때문이라고 생각했다.

Seq2Seq

• Sequence to Sequence 모델은 NLP 중 many-to-many 타입에 해당되는 모델이다

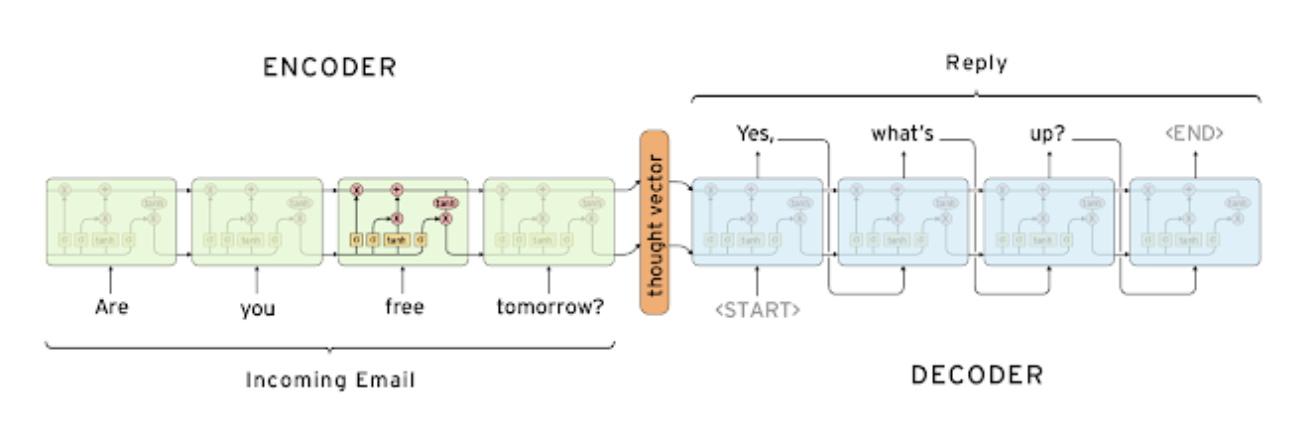
• 인코더와 디코더로 구성되어 인코더는 input을 받고 디코더는 output을 낸다.
• 서로 share하지 않는다.
• 세부구조를 보면 여기서는 lstm을 선택한 것을 볼 수 있다.
• 인코더 마지막 hidden state vector는 이전 타입 스텝의 hidden state 역할을 한다.
• 디코더에서는 시작 전 첫 토큰을 <SoS(Start-of-Sentence)>를 넣는다.
• 디코더에서 <EoS(End-of-Sentence)>가 나올때까지 생성한다.

RNN기반의 모델들은 hidden state vector의 dimension이 정해져있어서, 짧은 문장이든 긴 문장이든 마지막 타임스텝인 hidden state vector(주황색)에 앞서 나온 정보들을 모두 넣어야한다.
-> 매우 긴 문장이면 매우 압축된 형태, 앞부분 정보들이 많이 소실될 수 있다.

만약

I go home

을 모델에 넣는다면, I에 대한 정보가 유실될 수 있다. 그러면 주어에 대한 정보를 잃는 것이기 때문에 성능에 치명적인 영향을 준다.

=> 연구자들은 문장 순서를

home go I

식으로 바꾸는 방법을 제안하기도 하였다.

Attention

위의 문제를 해결하기 위해 attention 모델을 사용한다.

• 인코더의 마지막 스텝인 hidden state vector(주황색)에만 의존하는 것이 아니라,
  각 단어를 입력 받았을 때마다 나오는 hidden state를 모두 디코더에 넘겨, 디코더에서는 이를 선별적으로 가져다가 사용한다.

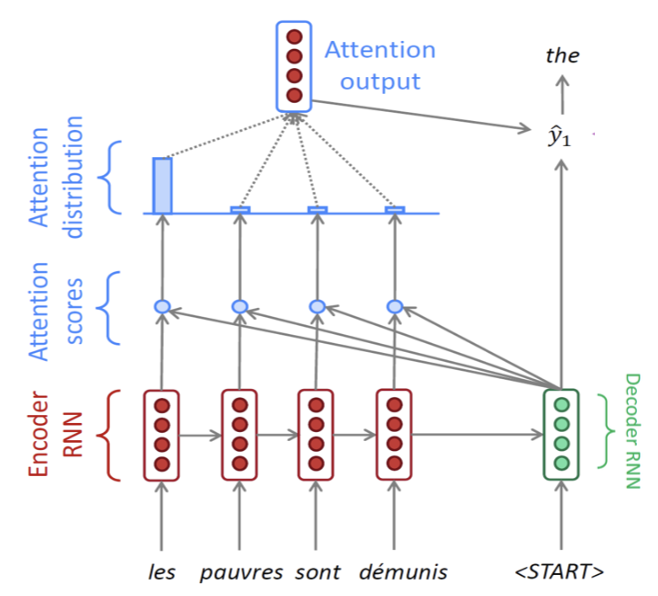
• 인코더에서 각 단어마다 hidden state가 만들어진다.
• 마지막 타임스텝이 디코더에 $h_0$에 입력으로 들어가고 <Start(SoS)>가 $x_1$으로 들어간다.
• 입력 받은 것을 바탕으로 디코더에서 $h_1^d$을 만든다.
• 단어들의 각 hidden state에서 선별적으로 정보들을 골라내는 과정을 수행하기 위해 각각 단어의 hidden state와 내적연산을 한다.
• 내적을 해서 나오는 값들을 유사도 score로 본다.
• 이 값들을 softmax를 통과시켜 확률값을 구한다.
• 이렇게 구한 확률값은 인코더의 가중치로 사용되고 가중 평균을 구할 수 있다.
• 마지막에 가중 평균된 벡터인 attention의 output과 디코더의 hidden state를 concat이 되어 output layer의 입력으로 들어간다.

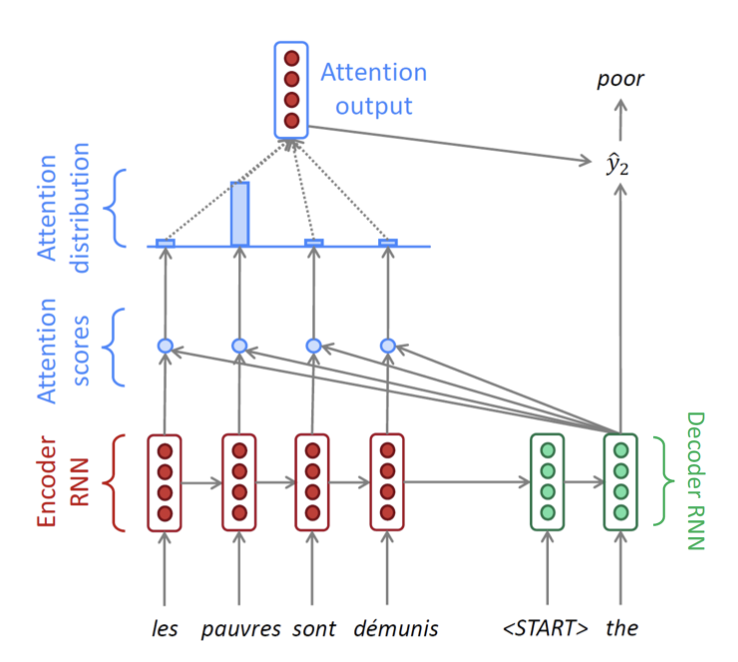
• 이전 디코더의 hidden state vector를 입력으로 받고 이전 output도 입력으로 받아 새로운 hidden state vector를 생성한다.
• 이전과 동일하게 각 단어의 hidden state vector와의 내적으로 유사도를 구하고 확률분포를 구한 후 인코더에 적용하여 output을 구한다.그리고 디코더 hidden state vector와 attention output을 concat하여 다음 결과를 만든다.

-> 중간 attention distribution벡터를 attention vector라고 부른다.

그때마다 서로 다른 가중치를 인코더 hidden state vector에 적용해서 나오는 가중평균된 벡터를 각 output layer에 입력으로 사용하여 예측 성능을 높인다.

디코더 hidden state 역활: attention 가중치 결정과 단어 예측을 위한 output layer의 입력

Teacher forcing

학습 할 때는 이전 예측된 결과를 학습에 쓰지 않고,
ground truth값을 넣어 잘못 학습되지 않도록 막는다.
-> 그러나 이 방식은 실제 test할 때의 상황과는 다르다.

그래서 초반에는 teacher forcing 방식을 이용하다가 어느 지점 이후에서는 사용하지 않는 방식도 존재한다.

Attention Score

Attention Score를 구하는 데는 3가지 방식이 있다.

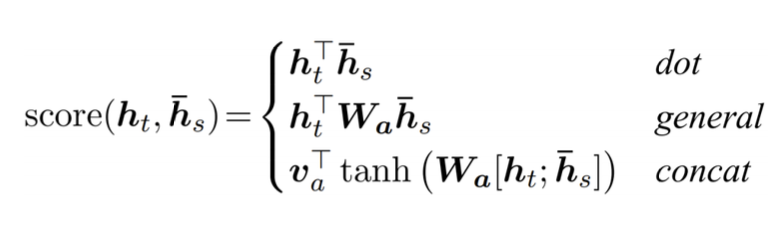
1) Dot은 말 그대로 dot product로 연산하는 것
2) general은 가운데 $W_a$를 두어 가중치 역할을 하도록 한다.
3) concat은 디코더 hidden state와 인코더 벡터를 concat하고 fully connected layer 하나를 두어 최종 스카라 값을 구한다. 이는 여러 layer로 확장할 수 있다.

기존 연산만을 통해 구해졌던 attention score가 학습 가능한 가중치 연산이 추가되었다.