소프트맥스, 활성함수, 역전파

소프트맥스 연산

모델의 출력을 확률로 해석할 수 있게 변환해주는 연산이다.

$softmax(o) = (\frac{exp(o_1)}{\sum_{k=1}^{p}exp(o_k)},\cdots,\frac{exp(o_p)}{\sum_{k=1}^{p}exp(o_k)})$

$\mathbb{R}^p$에 있는 벡터를 확률 벡터로 변환해준다.

아래의 파이썬 코드로 구현할 수 있다.

def softmax(vec):
	denumerator = np.exp(vec - np.max(vec, axis=-1, keepdims=True))
	numerator = np.sum(denumerator, axis=-1, keepdims=True)
	val = denumerator / numerator
	return val

⇒ exp연산이기때문에 오버플로우 발생할 수 있다. 그래서 vec에서 max를 빼준다. max를 빼준다고 하도 결과는 변하지 않는다.

• 추론 → 원핫벡터(소프트맥스 사용 x)
• 학습 → 소프트맥스

활성함수

비선형함수로 아래 함수들이 자주 사용된다.

ex) sigmoid, tanh, ReLU 등

신경망 = 선형모델과 활성함수를 합성한 함수

신경망이 여러층 합성되면 다층 퍼셉트론(MLP)이라고 한다.

이 과정이 순차적으로 계산되는 것을 순전파(forward propagation)라고 한다.

왜 층을 여러개 쌓을까?

이론적으로는 2층 신경망으로 근사할 수 있지만,
층이 깊을수록 목적함수를 근사하는데 필요한 뉴런의 숫자가 빨리 줄어든다.(적은 파라미터)
그렇다고 학습하기 쉬운 것은 아니다.

층이 얇으면 필요한 뉴런의 숫자가 기하급수적으로 늘어난다.

역전파 (backpropagation)

위층의 gradient를 계산하면서 아래층으로 전달하면서 이뤄진다.

체인룰을 기반으로 자동미분(auto-differentiation)을 사용한다.

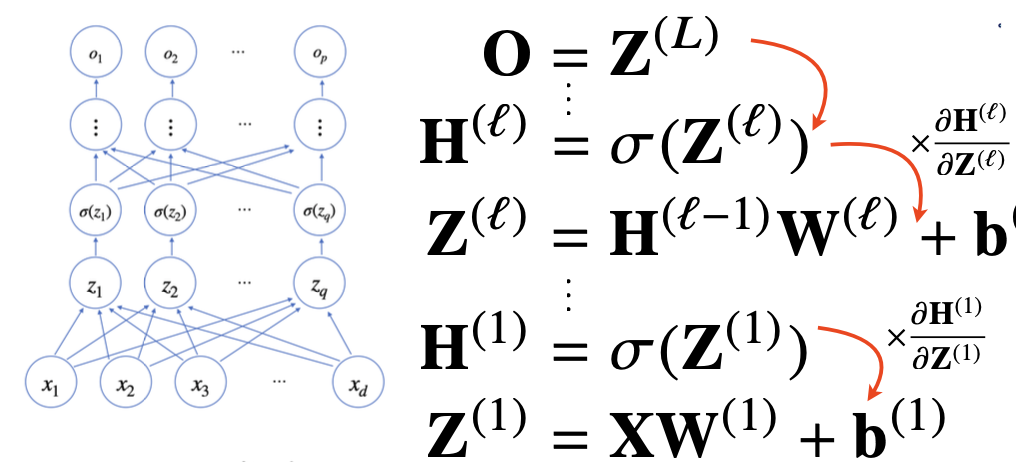
이때 각 노드의 텐서값을 컴퓨터가 저장해야 미분 계산이 되기 때문에 역전파가 순전파보다 많은 메모리를 사용한다.