[PyGAD] Genetic Algorithm (GA) : Neural Network Design for Regression [1]

Bobae·2023년 9월 7일

PyGAD

목록 보기

5/6

지난 포스팅까지 pygad.gann.GANN 모듈을 활용해서 classification 문제를 위해 NN(Neural Network)를 훈련하는 방법을 소개했습니다. PyGAD는 classification 문제 뿐만 아니라, regression 문제를 해결하기 위해 NN를 훈련하는 것을 지원합니다.

이번 포스팅에서는 simple regression 문제를 위해 NN을 훈련하는 방법을 소개하도록 하겠습니다.
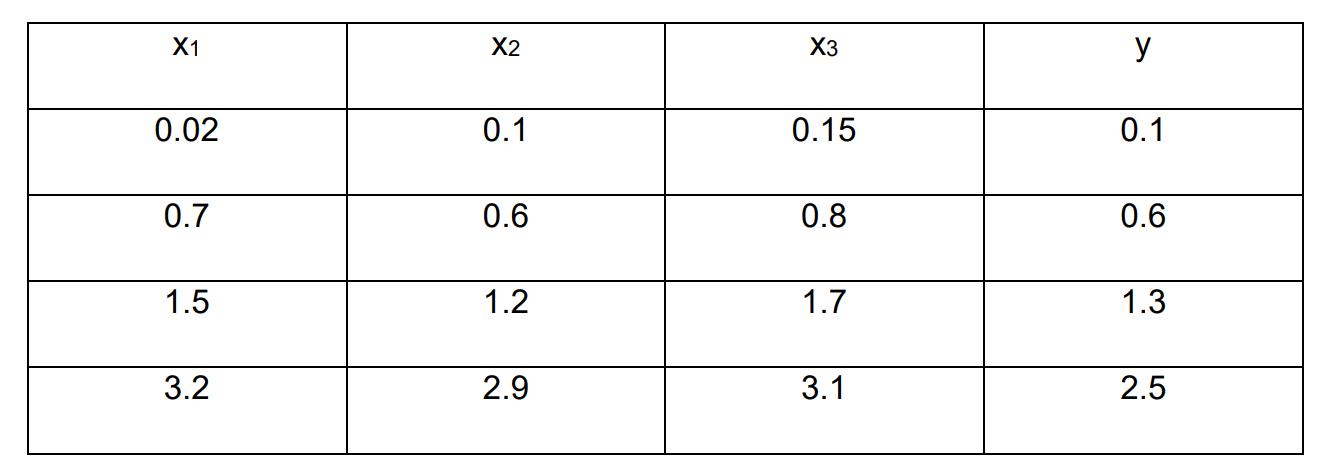
예시는, input 데이터 $x1, x2, x3$ 가 주어져있고 output 데이터 $y$ 를 예측하는 문제입니다.

진행과정은 classification 문제를 해결하는 것과 거의 동일한 과정으로 진행됩니다.

우선 라이브러리들을 다운받아줍니다.

!pip install pygad==2.17.0
import numpy
import pygad
import pygad.nn
import pygad.gann
import pandas

Training Dataset 준비

주어진 예제는 4개의 sample 데이터가 있고, 각 sample 데이터에 3개의 feature가 있는 경우입니다. 그렇기 때문에, input 데이터는 (4, 3) 구성을 가집니다.
output 배열에 대해서 각 요소는 샘플의 예측 데이터를 나타내는 하나의 숫자형 데이터로 표현되어야 합니다.

# Data inputs
data_inputs = numpy.array([[0.02, 0.1, 0.15],
                           [0.7, 0.6, 0.8],
                           [1.5, 1.2, 1.7],
                           [3.2, 2.9, 3.1]])

# Data outputs
data_outputs = numpy.array([[0.1],
                            [0.6],
                            [1.3],
                            [2.5]])

input의 수는 3개, output은 각 sample 데이터당 1개의 예측 결과를 가지므로 1개로 정의합니다.

num_inputs = data_inputs.shape[1]
num_output = 1

pygad.gann.GANN class의 인스턴스 생성

훈련 데이터를 준비하고 나서, pygad.gann.GANN 클래스의 인스턴스를 생성합니다. classification 문제를 위해 결과 값을 얻기 위해서는 softmax를 사용해서 각 클래스에 대한 probability를 추정해야 합니다. 하지만 Regression 문제에서는 output layer에서 활성화함수 처리를 해 줄 필요 없습니다.

# the NN configuration
num_solutions = 6 # population size of the GA.

GANN_instance = pygad.gann.GANN(num_solutions=num_solutions,
                                num_neurons_input=num_inputs,
                                num_neurons_hidden_layers=[2],  #the number of hidden nodes in the hidden layer
                                num_neurons_output=num_output,
                                hidden_activations=["relu"],
                                output_activation="None")

input layer와 hidden layer 사이에는 (number inputs x number of hidden neurons) = (3x2)와 같은 크기의 weights matrix가 있습니다.
hidden layer와 output layer 사이에는 (number of hidden neurons x number of outputs) = (2x1)와 같은 크기의 weights matrix가 있습니다.

Population Weights를 벡터화

population weights를 각 네트워크마다 하나씩 벡터로 보유하는 목록을 생성하려면 pygad.gann.population_as_Vectors() 함수가 사용됩니다.

population_vectors = pygad.gann.population_as_vectors(population_networks=GANN_instance.population_networks)
initial_population = population_vectors.copy()

Fitness Function 정의

해당 예시에서는 regression 문제를 위한 NN를 훈련하고 있으므로, problem_type="regression"으로 지정해줍니다.

def fitness_func(solution, sol_idx):
    global GANN_instance, data_inputs, data_outputs

    predictions = pygad.nn.predict(last_layer=GANN_instance.population_networks[sol_idx],
                                   data_inputs=data_inputs, problem_type="regression")
    solution_fitness = 1.0/numpy.mean(numpy.abs(predictions - data_outputs))

    return solution_fitness

Generation Callback Function 정의

# Set the fitness value of the previous generation.
last_fitness = 0

def callback_generation(ga_instance):
    global GANN_instance, last_fitness

    population_matrices = pygad.gann.population_as_matrices(population_networks=GANN_instance.population_networks,
                                                            population_vectors=ga_instance.population)

    GANN_instance.update_population_trained_weights(population_trained_weights=population_matrices)

    print("Generation = {generation}".format(generation=ga_instance.generations_completed))
    print("Fitness    = {fitness}".format(fitness=ga_instance.best_solution()[1]))
    print("Change     = {change}".format(change=ga_instance.best_solution()[1] - last_fitness))

    last_fitness = ga_instance.best_solution()[1].copy()

pygad.GA class를 활용하여 인스턴스 생성

num_parents_mating = 4 # Number of solutions to be selected as parents in the mating pool.
num_generations = 500 # Number of generations.
mutation_percent_genes = 5 # Percentage of genes to mutate. This parameter has no action if the parameter mutation_num_genes exists.
parent_selection_type = "sss" # Type of parent selection.
crossover_type = "single_point" # Type of the crossover operator.
mutation_type = "random" # Type of the mutation operator.
keep_parents = 1 # Number of parents to keep in the next population. -1 means keep all parents and 0 means keep nothing.
init_range_low = -1
init_range_high = 1

# the ga instance is set here:
ga_instance = pygad.GA(num_generations=num_generations,
                       num_parents_mating=num_parents_mating,
                       initial_population=initial_population,
                       fitness_func=fitness_func,
                       mutation_percent_genes=mutation_percent_genes,
                       init_range_low=init_range_low,
                       init_range_high=init_range_high,
                       parent_selection_type=parent_selection_type,
                       crossover_type=crossover_type,
                       mutation_type=mutation_type,
                       keep_parents=keep_parents,
                       callback_generation=callback_generation)

GA 실행

ga_instance.run()

output:

Generation = 1
Fitness    = 0.8982586714613423
Change     = 0.8982586714613423
Generation = 2
Fitness    = 0.903182824693004
Change     = 0.004924153231661732
Generation = 3
Fitness    = 0.903182824693004
Change     = 0.0
...
Generation = 500
Fitness    = 70.80114858632587
Change     = 0.0

Plot results 확인

ga_instance.plot_result()

Best Solution 정보

# Returning the details of the best solution.
solution, solution_fitness, solution_idx = ga_instance.best_solution()
print("Parameters of the best solution : {solution}".format(solution=solution))
print("Fitness value of the best solution = {solution_fitness}".format(solution_fitness=solution_fitness))
print("Index of the best solution : {solution_idx}".format(solution_idx=solution_idx))

output:

Parameters of the best solution : [-0.74939306  0.49861493  1.0162775   0.10788315 -0.15686854  0.61086612
 -0.84186043  0.68106809]
Fitness value of the best solution = 70.80114858632587
Index of the best solution : 0

if ga_instance.best_solution_generation != -1:
    print("Best fitness value reached after {best_solution_generation} generations.".format(best_solution_generation=ga_instance.best_solution_generation))

output:

Best fitness value reached after 495 generations.

Trained Weights를 사용해서 예측

결과 값을 예측 하기 위해 problem_type="regression"을 지정해줍니다.

# Predicting the outputs of the data using the best solution.
predictions = pygad.nn.predict(last_layer=GANN_instance.population_networks[solution_idx],
                               data_inputs=data_inputs,
                               problem_type="regression")
print("Predictions of the trained network : {predictions}".format(predictions=predictions))

우리가 예측하고자 했던 $y$ 값 $[0.1, 0.6, 1.3, 2.5]$ 에 거의 converge한것을 확인할 수 있습니다.
output:

Predictions of the trained network : [array([0.06660701]), array([0.60698703]), array([1.28953727]), array([2.49434649])]

통계 계산

에러율을 확인하여 우리가 훈련한 NN모델의 performance를 확인할 수 있습니다.

#the searching result is shown
abs_error = numpy.mean(numpy.abs(predictions - data_outputs))
print("Absolute error : {abs_error}.".format(abs_error=abs_error))