2강. Image Classification Pipeline
Image Classification에 활용되는 KNN(K-Nearest-Neighbor)의 원리와 한계, 그리고 Linear Classificatier의 개념에 대한 내용이었습니다.
CS231N - 2강
- Challenges in Image Classification
- K-Nearest-Neighbor
- Linear Classificatier
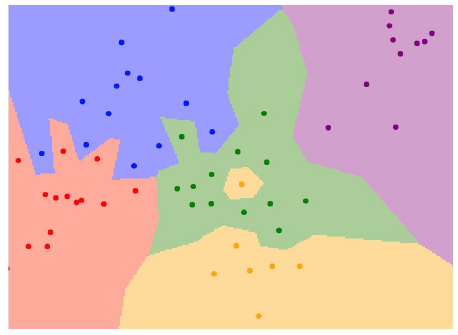
Challenges in Image Classification
Image Classification을 위해서는 Image Data 처리에 다양한 변수와 환경을 고려해야 하기에 그 난이도가 높습니다.
Viewpoint Variation (시점 변동성)
Image가 촬영된 각도가 각 Image 마다 상이할 수 있기 때문에 카메라 각도를 고려하여 Classification을 진행해야 합니다.
Illumination (조명)
피사체를 비추는 조명의 방향과 밝기에 따라 Image의 상이 다르게 맺힐 수 있습니다.
Deformation(형태의 변형)
같은 Class로 인식돼야 하는 피사체라도 대상이 취하고 있는 자세, 위치, 형태가 달라진다는 점을 고려해야 합니다.
Occlusion (점유율)
피사체가 Image 내에서 차지하고 있는 비율, 그리고 Image 상에 드러나 있는 피사체의 일부 등 부분적인 Image 만으로 Classification이 가능해야 합니다.
Background Clutter (배경 유사도)
피사체와 피사체 주위 배경의 색상이나 질감이 유사하여 Image Classification이 제대로 이루어지지 않을 수도 있습니다.
Intra Variation (형태 다양성)
같은 Class의 피사체가 한 Image 안에 있을 때, 그들의 형태가 다 다른 경우에도 같은 Class로 분류하도록 하는 과정이 필요합니다.
결론
다양한 Image Challenge에 대응할 수 있도록 여러 Image Data를 토대로 한 Classification 판단이 이루어져야 합니다.
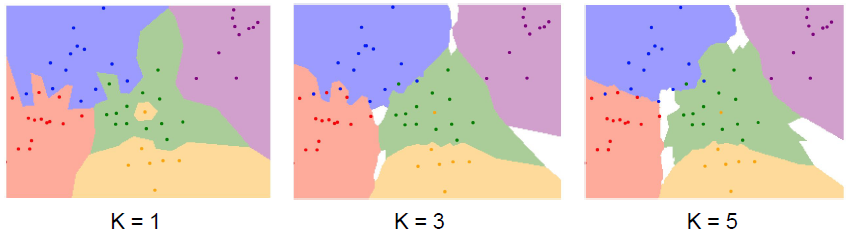
KNN (K-Nearest-Neighbor)
KNN은 해당 Image Data와 유사한 Data들이 어떤 Class로 분류되었는지를 참조해 Class를 결정하는 방법론입니다.
Image Data의 형태
Metric Data (행렬 데이터)
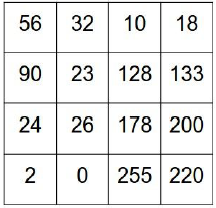
행과 열로 이루어진 NxN 차원의 데이터로 일반 수열 데이터에 비해 많은 양의 정보를 담을 수 있다는 장점이 있어 Image Data를 다룰 때 주로 사용됩니다.
Image Classification의 과정
Image Classification은 Training과 Pridiction 두 가지의 과정으로 이루어집니다.
1. Training (학습)
여러가지 특성과 형태의 Image Data를 주어진 Class에 대해 수집하고, 그 데이터를 저장합니다.
2. Prediction (예측)
저장된 Image Data들을 기반으로 새로운 Image Data의 Class를 예측합니다.
NN (Nearest Neighbor)
Test Data와 Training Data 사이의 차이값을 Data 간 Distance로 저장하고, Distance가 가장 짧은 Data의 Class를 예측값으로 취하는 방식입니다.
1. Train
각 Image Class에 해당하는 Data들을 입력받고 그 Metric Data 값을 저장합니다.
시간복잡도 O(1):
입력값의 저장은 Data 한 개 당 하나씩 즉각적으로 이루어집니다.
2. Test Data Input
Image Classification의 대상이 되는 Test Data의 Meric Data 값을 입력받습니다.
3. Distance 계산
입력받은 Test Data와 저장된 모든 Train Data 간의 Distance 계산을 진행합니다.
시간복잡도 O(N)
한 개 Test Data 당 모든 Train Data와의 연산이 필요합니다.
4. Predict
연산된 Distance 값 중 가장 작은 값을 가지는 Data의 Class, 다시말해 Test Data와 가장 유사한 Train Data의 Class 값을 예측값으로 취합니다.
실행 결과
KNN (K-Nearest Neighbor)
Distance가 가장 작은 Train Data의 Class만이 아닌, K번째로 작은 Data의 Class까지 참조해 예측값을 결정하는 방법입니다.
NN의 한계
가장 작은 Train Data의 Class만을, 다시 말해 예측의 근거가 되는 데이터가 하나 뿐이기 때문에 분류 시 Overfitting 문제가 발생할 수 있습니다
Majority Vote (우선순위 투표)
최소 Distance Train Data만이 아니라, K번째로 작은 Data까지 참조해 더 많이 분포하는 Class로 예측값을 결정합니다.
이때, 저 작은 Distance를 가질수록 투표 시 가중치를 더해 연산합니다.
실행결과
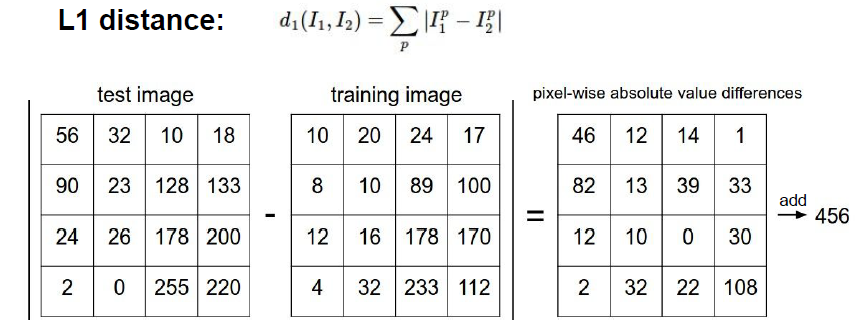
Distance Metric
Data 간의 Distance를 구하는 방법은 L1 Distance와 L2 Distacne가 있습니다.
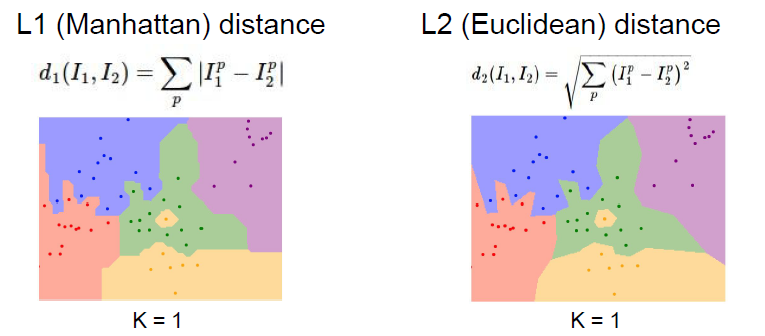
- L1 Distance
Test Data와 Train Data간 Metric Data 값의 차이에 절대값을 취하는 방법으로 Coordinate System(좌표계)의 영향을 크게 받아 Classification 결과가 직선을 띱니다. - L2 Distance
L1처럼 Metric Data 값의 차이를 연산하돼, 그 값을 제곱하여 더한 이후, 제곱근 연산을 통해 거리를 구하는 Euclidean Distance 방식으로 Classification 결과가 곡선을 띱니다.
Hyperparameter
Classification 연산에 필요한 선입력값으로 학습 진행자가 결정해줘야 하는 값입니다.
Ex. K값, Distance 연산 방식(L1,L2) etc
1. Hyperparameter setting

해당 Image Classification 문제에 적합한 K값을 선택합니다.
이때, K값이 1일 경우 Overfitting의 가능성이 있습니다.
2. Split Data - Train/Test

주어진 Data를 Image Training에 쓰이는 Train Data와 Classification Test에 쓰이는 Test Data로 분할합니다.
3. Split Data - Train/Validation/Test

Train Data를 Train Data와 최적 Hyperparameter 도출에 쓰이는 Validation Data로 분할합니다.
4. Cross Validation

Hyperparameter가 평균적인 Train Data 값들에 대해 도출되도록 Train Data를 N개의 Fold Data로 나누고, 각 Fold를 Validation Data로 활용하면서 최적의 Hyperparameter를 찾습니다.
KNN의 한계
-
Distance 값의 효용성
Metric Data 값의 차이인 Distance로는 이동, 색상변화, 장애물 등 Image Data가 가지고 있는 정보를 유추할 수 없습니다. -
느린 속도
Test의 시간복잡도가 O(N)이기 때문에 4차원, 5차원 등 고차원 데이터에 대해서 Classification 수행 속도가 현저히 느립니다.
결론
Image Classification에 KNN의 성능은 낮습니다.
Linear Classification
Linear Classification(선형 분류)는 선형 회귀식 연산값을 토대로 Class를 판정하는 방법론입니다.
Linear Classifier
Linear Classifier는 Image Metric Data, Weight, Bias로 이루어져 있습니다.
Linear System
Linear System (선형 시스템)은 회귀계수(변수 X의 계수)의 값에 따라 그 연산값이 달라지는 수식입니다.
Linear Classifier의 구성
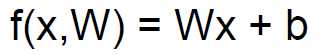
Linear Classifier (선형 분류기)는 독립변수 X, Parameter 회귀계수 W(Weight), 오차 Bias로 이루어져 있습니다.
- N: Image Data의 크기
- M: Class의 개수
- X: Image Metric Data가 입력되는 Nx1 크기의 독립변수입니다.
- W: 회귀계수로 MxN 크기의 Metric Data입니다.
- Bias: 연산값의 오차를 조정해주는 Mx1 크기의 Data입니다.
Linear Classifier의 원리
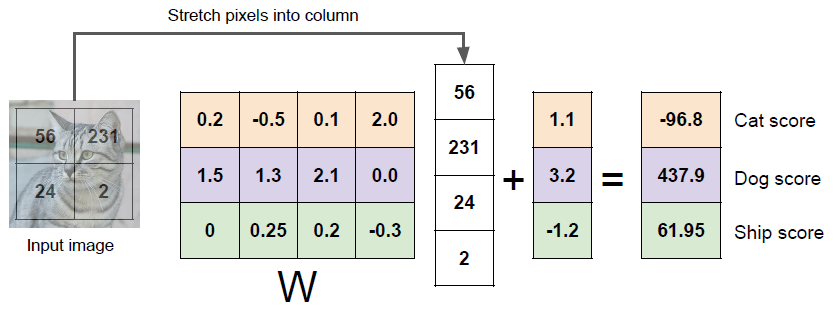
Linear Classifier 연산은 변수들 간의 행렬곱, 행렬합으로 이루어집니다.
1. Image Data 대입
Linear Classifier의 독립변수 X 자리에 Image Metric Data를 Nx1 크기로 대입합니다.
2. W-X 행렬곱
MxN 크기 행렬 데이터, W와 X간의 행렬곱을 통해 Mx1 크기 행렬 데이터를 구합니다.
3. Bias 행렬합
행렬곱 연산을 통해 구한 행렬 데이터와 Bias 간의 행렬합을 통해 오차를 보정합니다
4. Class Score 확인
행렬합의 결과인 Mx1 행렬데이터의 각 행은 해당 Image가 각 Class에 속할 가능성을 나타냅니다.
5. Class 결정
Class Score 값 중 가장 큰 값을 가지는 행의 Class를 최종 Class로 취합니다.
Linear Classifier의 한계
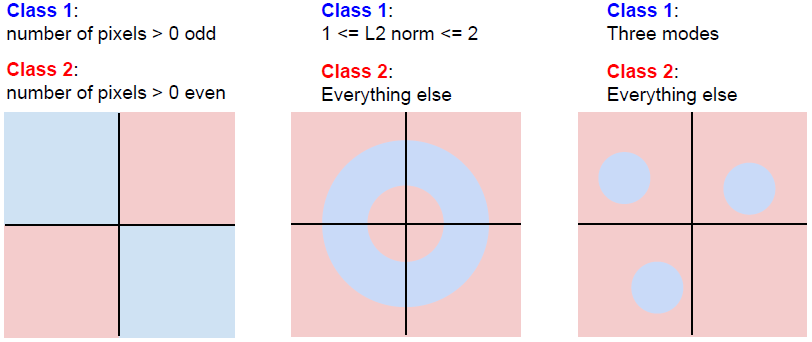
- 비선형 데이터 취약성
Linear Classifier는 Linear System이 나타내는 회귀직선을 기준으로 하여 Data들을 서로 다른 Class로 분류하는 방식으로 이루어집니다.
하지만, 위 사진처럼 직선으로 서로 다른 Class의 분류가 불가능한 경우에는 Classifier가 상당히 복잡해지고, 이에 따라 Overfitting의 위험성이 커진다는 한계가 있습니다.
결론
Linear Classifier의 단독 사용으로는 비선형 Data에 대한 Classification이 어렵습니다.
오역, 오류 등의 지적은 언제나 환영입니다