동적계획법(Dynamic Programming) 정리글_Python

앙금빵·2021년 5월 21일

자료구조와 알고리즘

목록 보기

2/5

동적 계획법

이미 진행이 되었던 연산이 반복되는 결점을 보안하기 위해 동적 계획법(Dynamic Programing, DP)가 고안되었다. 여러 개의 소문제로 분할하여 각 소문제의 해결안을 바탕으로 주어진 문제를 해결, 이때 각 소문제는 다시 여러개의 소문제로 분할 가능하다.

처음 진행되는 연산은 기록
이미 진행됬던 연산이라면 다시 연산이라면 기록되어 있는 값을 호출
시간 & 자원절약 가능

DP를 이해하기 위해 아주 좋은 예시인 피보나치 수열을 알아보자.

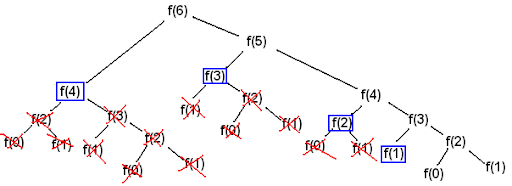
피보나치 수

자료출처: 위키피디아

피보나치 수 코드 구현

피보나치_재귀적 풀이: O( $2^n$ )

def pibonacci_recur(n):
    if n>=2:
        return pibonacci_recur(n-1) + pibonacci_recur(n-2)
    else: 
        return n

n=int(input("n값을 입력하세요"))

print(pibonacci_recur(n)) # n번째 피보나치 수열항 출력

[재귀방식] 피보나치 수열항 컴퓨터가 구하는 과정

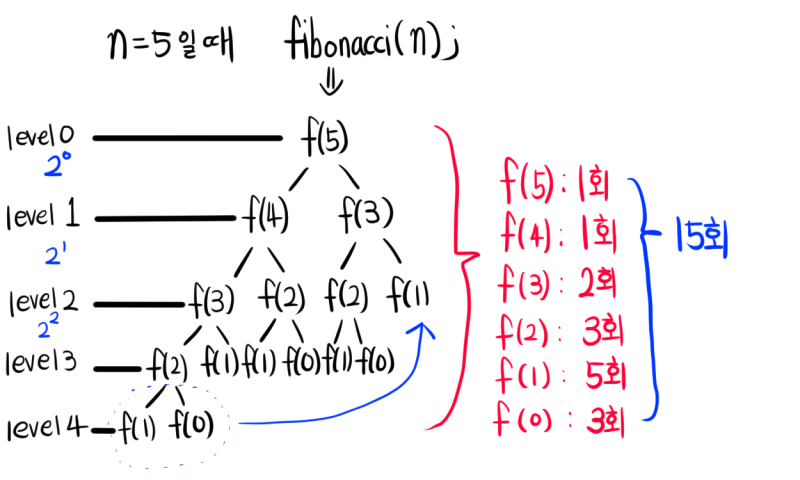
재귀 호출을 트리 구조로 나타내면 윗 그림과 같이 나타내 진다. (n=5)

level 3레벨에서 덧셈연산을 level 4에서 채우면 n-2 level = level 3 까지 덧셈연산을 한다고 볼 수 있다.

즉, 덧셈 연산을 $2^0 + 2^1 + 2^2$ + ··· + $2^{n-4}$ $+ 2^{n-3}+2^{n-2}$ 번 이루어지고

등비 수열 공식을 적용하면 $2^{n-2} -1$ 로 나타낼 수 있다.

따라서, 시간 복잡도는 O( $2^n$ )로 나타낼 수 있다.

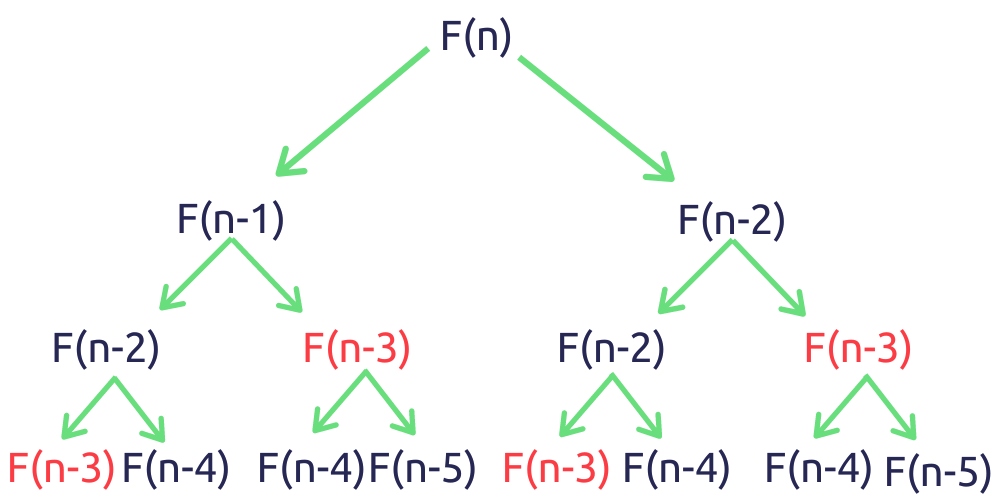
피보나치_동적 계획법

연산이 반복되는 결점을 보안하기 위해 동적 계획법(Dynamic Programming, DP)가 고안되었다.

앞서 동적 계획법은 소문제의 해를 따로 저장해서 나중에 다시 사용한다고 언급을 하였다.

이렇게 중복 연산을 방지하는 방법에는 2가지 방법이 있다.

1. Memoization (Top-Down, 하향식)

하향식(Top-Down) 경우 하위 문제에 대하여 정답을 계산했는지 확인해가며 문제를 자연스럽게 풀어나가는 방법이다. 흔히 이를 Memoization이라고 부른다.

# DP, Memoization

dp_Memo=[0]*11
dp_Memo[0]=1
dp_Memo[1]=1

def fib_Memo(n):
    
    #한번도 계산한 적이 없는 경우
    
    if dp_Memo[n]==0: #dp list에 계산한적이 없는경우 0으로 저장되어 있음
        dp_Memo[n] = fib(n-1)+fib(n-2) #재귀로 계산하여 리스트에 값 추가
    
    # 새롭게 추가 값 혹은 저장된 값 반환
    
    return dp_Memo[n]

# 피보나치 수열 항 리스트 전체 출력
for i in range(11):
    fib_Memo(i)

print(dp_Memo)

fib_Memo(10)

"""
[1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89]
output: 89
"""

2. Tabulation (Bottom-up, 상향식)

상향식(Bottom-Up)은 더 작은 하위 문제부터 살펴본 다음 작은 문제의 정답을 이용하여 큰 문제의 정답을 풀어나가는 방법이다.

#DP, Tabulation(Bottom-Up, 상향식)

# 풀이 1.
def fib_Tab1(n):
    
    dp_Tab=[0]*(n+1)
    dp_Tab[0],dp_Tab[1]= 1,1
    
    # 작은 값(소문제)부터 직접 계산하며 진행
    
    # 2항 ~ n항 까지 피보나치 수열항 계산 (0,1 항 = 1)
    for i in range(2,n+1):        
        dp_Tab[i]=dp_Tab[i-1]+dp_Tab[i-2]
    
    print(dp_Tab) # 피보나치 수열 항 리스트 전체 출력
    
    return dp_Tab[n]

fib_Tab(10)

"""
[1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89]
output: 89
"""

#DP, Tabulation(Bottom-Up, 상향식)

# 풀이 2.

def fib_Tab2(n):
	p=[1,1]
	for i in range(2,n+1): # n번째 까지 피보나치 수열 나열
		p.append(p[-1]+p[-2]) # 마지막 2 요소의 합을 리스트에 추가
		print(p)
	return(p[-1]) #피보나치 n번째 값 Return

fib_Tab2(10)
"""
output: 89
"""