문제
효주는 포도주 시식회에 갔다. 그 곳에 갔더니, 테이블 위에 다양한 포도주가 들어있는 포도주 잔이 일렬로 놓여 있었다. 효주는 포도주 시식을 하려고 하는데, 여기에는 다음과 같은 두 가지 규칙이 있다.
- 포도주 잔을 선택하면 그 잔에 들어있는 포도주는 모두 마셔야 하고, 마신 후에는 원래 위치에 다시 놓아야 한다.
- 연속으로 놓여 있는 3잔을 모두 마실 수는 없다.
효주는 될 수 있는 대로 많은 양의 포도주를 맛보기 위해서 어떤 포도주 잔을 선택해야 할지 고민하고 있다. 1부터 n까지의 번호가 붙어 있는 n개의 포도주 잔이 순서대로 테이블 위에 놓여 있고, 각 포도주 잔에 들어있는 포도주의 양이 주어졌을 때, 효주를 도와 가장 많은 양의 포도주를 마실 수 있도록 하는 프로그램을 작성하시오.
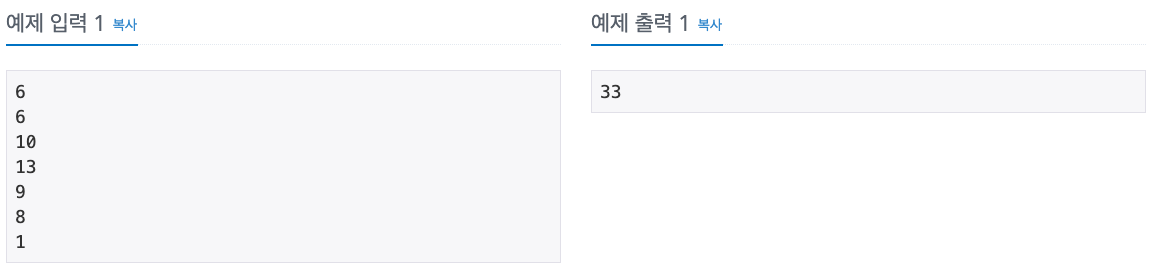
예를 들어 6개의 포도주 잔이 있고, 각각의 잔에 순서대로 6, 10, 13, 9, 8, 1 만큼의 포도주가 들어 있을 때, 첫 번째, 두 번째, 네 번째, 다섯 번째 포도주 잔을 선택하면 총 포도주 양이 33으로 최대로 마실 수 있다.
입력
첫째 줄에 포도주 잔의 개수 n이 주어진다. (1≤n≤10,000) 둘째 줄부터 n+1번째 줄까지 포도주 잔에 들어있는 포도주의 양이 순서대로 주어진다. 포도주의 양은 1,000 이하의 음이 아닌 정수이다.
출력
첫째 줄에 최대로 마실 수 있는 포도주의 양을 출력한다.
어떻게 풀 것이냐?
과정을 생략하고 코드를 보고싶은 분은 여기로
기본 입출력 정의
#include <iostream>
#include <algorithm>
using namespace std;
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int t;
cin >> t;
int arr[t];
for (int i = 0; i < t; i++) {
cin >> arr[i];
}
for (int i = 0; i < t; i++) {
cout << arr[i] << " ";
}
cout << endl;
}접근 방식
계단문제(BOJ:2579번)와 비슷하다고 생각했다. 연속해서 3개의 포도잔을 마실 수 없다 == 연속해서 계단 3개를 오를 수 없다.
동적 프로그래밍을 사용하는 문제에서는 보통 연속해서 3개의 어떤 행위를 할 수 없는 것 같다.
최대의 포도주를 시식해야되니까(😏 주당이네) i 번째의 행위를 할 때, 최고의 i-1 또는 i-2번째 행위를 고려하면 된다. DP의 식을 세워야 한다.
3번째 포도주를 마실때를 생각해보자. 1 번째, 2 번째, 3 번째 순서대로 전부 마시고 싶지만,,,, 취하니까 못먹게 하나보다. 그렇다면 생각해야한다. 1번째, 3번째 포도주를 마실것이냐! 아니면 2번째, 3번째 포도주를 마실것이냐! 이 생각부터 시작했다. 1 → 3으로 연속적이지 않게 포도주를 마실것인지, 2 → 3으로 연속으로 포도주를 마실 것인지 생각을 해야한다! 그렇다면 좀 더 자세히 생각해보자.
- i 번째 포도주를 마실 때, 연속 첫번째로 마시는 경우, i-2번째의 DP값에 현재 포도주 양을 더한다.
- i 번째 포도주를 마실 때, 연속 두번째로 마시는 경우, i-1번째의 DP값에 현재 포도주 양을 더한다.
즉, DP배열은 2차원 배열로 필요할 것 같다.
dp[i][0] → i 번째 포도주를 첫 번째로 마시는 경우
dp[i][1] → i 번째 포도주를 두 번째로 마시는 경우
dp[i][0] → i 번째 포도주를 첫번째로 마시는 경우! i-1 번째 포도주는 마시면 안된다! 그러므로 i-2번째의 포도주를 마시는데, i-2 번째의 포도주를 어떻게 먹든 최대값으로 먹는 경우를 골라야 하니
max( dp[i-2][0](첫번째로 마신 경우), dp[i-2][1](두번째로 마신 경우) )
둘중에서 큰 값을 골라보자.
int dp[t][2];
dp[0][0] = arr[0];
dp[0][1] = 0;
dp[1][0] = arr[1];
dp[1][1] = dp[0][0] + arr[1];
for(int i=3;i<t;i++){
//dp[i][0] => i번째 요소를 처음 선택하는 경우
dp[i][0] = max(dp[i-2][0],dp[i-2][1]) + arr[i];
//dp[i][1] => i번째 요소를 2번째로 선택하는 경우
dp[i][1] = dp[i][0] + arr[i];
}
// t번째에서 큰걸 고른다.
cout<<max(dp[t-1][0],dp[t-1][1]);오잉...틀렸다.
뭐가 잘못된 걸까?? 😰
어디서, 뭐가 잘못된거지...?
일단 오타가 있었다.
dp[i][1] = dp[i][0] + arr[i]; → dp[i][1] = dp[i-1][0] + arr[i];
그랬더니 값이 더 이상하게 나온다. 😭
두번째 오타를 발견했다.
for문의 i 가 3부터 시작한다. → for 문의 i를 2로 바꿔줘야한다.
어쩐지 쓰레기값이 계속 나오더라.
근데 t번째가 29, 32이다! 왜지?
생각을 해봤더니...
굳이 t번째가 마지막이 될 필요가 없지 않나? t-1번째가 마지막이 되어도 되잖아?
예제도 그렇다. t번째가 1이니까
t-1번째를 못먹고 t를 먹기보다는
t를 포기하고 t-1번째를 먹는다!
이렇게 될 수 있다고 생각했으니 dp[t] 와 dp[t-1]중에서 max를 고르면 되겠다.
코딩해보자.
int a = max(dp[t-1][0],dp[t-1][1]);
int b = max(dp[t-2][0],dp[t-2][1]);
cout<<max(a,b)<<endl;이거지 이거지 👺
정답이다!
이제 제출하기 전에 체크하자 (특히 범위....주유소 문제에서 호되게 당했다.)
- 입력값과 출력값의 범위가 주어진 자료형(Int) 를 초과하는가?
1 ≤ n ≤ 10,000, 0 ≤ 포도주의 양 ≤ 1,000이니 최대 SUM은 1,000 ✖️ 10,000 = 10,000,000(천만)이니 초과 X 인 것 같다(확실하지 않음...) - 최소값을 입력 받았을 때, 최대값을 입력 받았을 때 잘 동작하는가?
최소값 : 1을 입력 받았을 때!
그렇다. 마지막에 dp[i-1]을 탐색하기 때문에 쓰레기값이 나온다. 수정하자.
int a = max(dp[t-1][0],dp[t-1][1]);
int b = 0;
if(t == 1){
b = 0;
}else{
b = max(dp[t-2][0],dp[t-2][1]);
}
cout<<max(a,b)<<endl;최대값은 테스트가 힘드니까...(10,000 번 입력할꺼야? 👊 💢 )
-
반례가 있는가?
일단 생각나는건 없다!
처절한 실패....
2%에서 틀렸다. 기억하자.
3. 반례. 연속으로 안 먹는 경우.
누군가 말했다. 안먹을 수 도 있다고..... 😢 아니 왜 안먹고 그르세요...
200 400 1 2 400 500 인 경우를 생각해보면 1, 2를 먹는건 손해 of 손해다. 나도 그렇게 생각한다. 분명히 안먹고 지나가는 경우가 있다.
그렇다면 또 생각해야 하는건 3번 이상 안먹고 지나가는 경우가 있나? → 200 400 1 1 1 400 500인 경우에는 중간에 1을 고르고 가면 되니까....3번 이상 안먹고 지나가는 경우는 없다! 라고 생각했다.
그럼 바로 코딩해보자.
2번이상을 연속으로 안먹는 경우? → 구글링을 통해서 해법을 찾았다.
dp[i] = max(dp[i],dp[i-1])이라고 한다
왜 그런지 솔직히 아직까지 이해가 안된다. 400을 고르는 순간에 2를 고른것과 비교를 한다?
나는 아직 많이 부족한 것 같다. 더 열심히 공부하자.
👨💻FULL CODE👨💻
#include <iostream>
#include <algorithm>
using namespace std;
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
int t;
cin >> t;
int arr[t];
for (int i = 0; i < t; i++) {
cin >> arr[i];
}
// for (int i = 0; i < t; i++) {
// cout << arr[i] << " ";
// }
// cout << endl;
int dp[t][2];
dp[0][0] = arr[0];
dp[0][1] = 0;
dp[1][0] = arr[1];
dp[1][1] = dp[0][0] + arr[1];
for(int i=2;i<t;i++){
//dp[i][0] => i번째 요소를 처음 선택하는 경우
dp[i][0] = max(dp[i-2][0],dp[i-2][1]) + arr[i];
//dp[i][1] => i번째 요소를 2번째로 선택하는 경우
dp[i][1] = dp[i-1][0] + arr[i];
//세개 이상을 안 고르고 건너뛸 수 있나? -> 세개 이상은 건너뛸 필요가 없다. 중간을 고르면 되그등요
dp[i][0] = max(dp[i][0],dp[i-1][0]);
dp[i][1] = max(dp[i-1][1],dp[i][1]);
}
int a = max(dp[t-1][0],dp[t-1][1]);
int b = 0;
if(t == 1){
b = 0;
}else{
b = max(dp[t-2][0],dp[t-2][1]);
}
cout<<max(a,b)<<endl;
return 0;
}💪FEED BACK🧗
- 계단문제랑 비슷한 줄 알았더니만 dp[i] = max(dp[i],dp[i-1])이라는 함정이 숨어있었다.
- 계단을 오르는 경우에는 무조건 밟지 않으면 올라갈 수 없다. (무조건 연속적으로 밟아야 한다.)
- 포도주 같은 경우 마셔도 되고 안마셔도 된다. 마시지 않는 것이 오히려 최대가 될 수 있다. (연속적이지 않을 수 있다!)
왜 dp[i] = max(dp[i],dp[i-1]) 이렇게 되는지를 고민해야겠다.
- 마지막 검토하는 순서를 만들었다.
1) int범위 확인
2) 최솟값과 최댓값 확인
3) 반례 확인
추가로 검토방법들을 만들어야겠다. 어처구니 없는 실수를 하지 않기 위해서. - 나는 아직 많이 부족하구나...이해를 못하다니
