[cs231a] Camera Models

Lecture 2: Camera Models
이 강의는 카메라 모델에 대해 다루고 있다.
(핀홀 카메라, 렌즈와 카메라의 기하학적 관계 등)

1. Pinhole Cameras

• 핀홀 카메라의 기본 원리와 구성: object 앞에 film을 놓아보자!
  
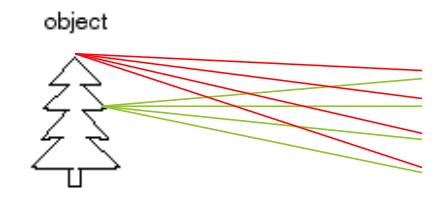
  필름을 통해 물체에서 나오는 빛을 직접 받아 이미지를 형성하는 방식이다.
• Aperture(조리개)의 역할과 중요성: 광선 중 대부분을 차단하는 barrier를 설치하자!
  barrier를 추가해서 대부분의 광선을 차단하면 이미지의 블러가 줄어든다. 이 barrier의 작은 개구 부분을 조리개(aperture)라고 한다. 조리개는 카메라 렌즈의 빛을 텍스트통제하여 이미지를 선명하게 만들어준다.

2. Camera History

• Leonardo da Vinci(레오나르도 다 빈치)가 최초로 기록한 Camera Obscura(카메라 옵스큐라) 개념을 소개
• Johann Zahn(요한 자흔)과 Joseph Nicéphore Niépce(조제프 니세포르 니엡스)가 최초의 휴대용 카메라 및 사진을 개발한 과정
• 사진의 발전과정, Daguerréotypes(다게레오타입) 및 Color Photography(컬러 사진)의 출현

3. Pinhole Perspective Projection

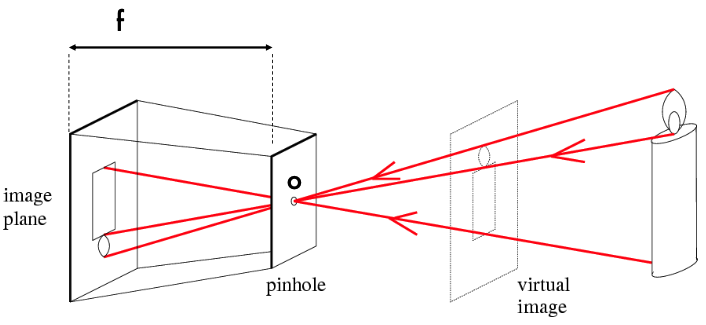
핀홀 카메라는 작은 구멍인 핀홀을 통해 빛이 들어와 이미지가 형성된다.
실제 물체의 각 점에서 나오는 빛이 핀홀을 통과하여 반대 쪽의 이미지 평면에 투영된다.
투영 과정을 통해 3물체가 2D 이미지로 변환된다.

3.1 투영방정식

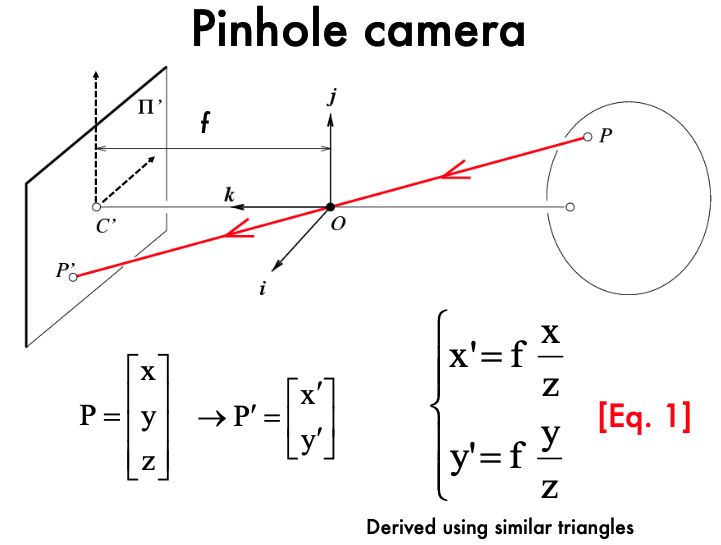
핀홀 카메라에서 이미지 평면에 투영된 점 $(x', y')$, 물체의 실제 3D 위치 $(X, Y, Z)$

$x' = \frac{fX}{Z}$
$y' = \frac{fY}{Z}$
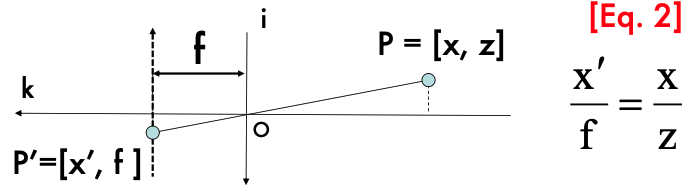
- $f$는 카메라의 초점 거리(focal length)
- $Z$는 물체의 깊이(depth)
- $(X, Y, Z)$는 물체의 실제 3D 좌표
- $(x', y')$는 이미지 평면에서의 2D 좌표

투영 방정식은 3D 공간의 점을 2D 평면으로 변환하는 기하학적 변환이다.
이 변환의 핵심은 원근법(perspective)이다.
- 원근법: 물체가 카메라에서 멀어질수록 이미지에서의 크기가 작아지는 현상
- 1. 3D 공간의 점 $(X, Y, Z)$에서 빛이 핀홀을 통과하여 반대쪽 평면에 투영된다.
- 2. 이 투영 과정에서, $Z$ 값에 따라 물체의 크기와 위치가 조정된다.
- 3. 변환된 2D 좌표 $(x', y')$는 실제 이미지로 나타나게 된다.

이미지에서 각 점이 어떻게 계산되고 위치가 정해지는질까?
카메라가 물체에 가까울수록 $Z$ 값이 작아지고, 이는 $(x', y')$ 값이 커져 이미지에서 물체가 더 크게 보이는 효과를 준다.

3.2 핀홀 카메라에서 조리개 크기의 중요성

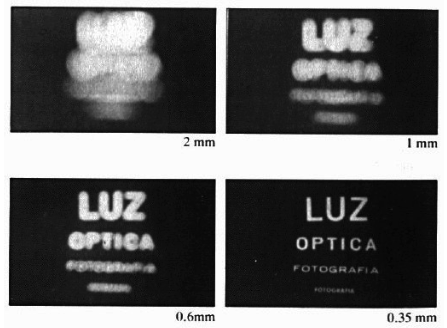
• 핀홀 카메라에서 물체의 빛이 작은 핀홀을 통과하여 필름에 도달한다. 이때 조리개(aperture)의 크기가 이미지의 선명도에 큰 영향을 미친다.
• 조리개 크기가 클 경우, 더 많은 빛이 통과하지만 이미지가 흐릿해진다.
• 조리개 크기가 작을 경우, 빛의 양이 제한되어 선명한 이미지를 얻을 수 있지만, 너무 작으면 충분한 빛이 들어오지 않아 어두운 이미지가 될 수 있다.
  렌즈를 추가하면 빛의 양을 조절하고, 이미지를 더 선명하게 만들 수 있다.

4. Cameras & Lenses

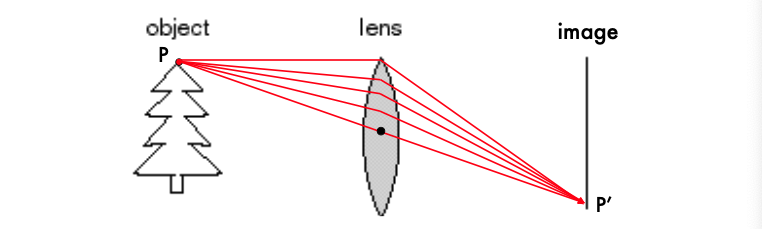
렌즈의 역할과 Focal Length(초점 거리): 렌즈의 기본 기능은 물체에서 나온 빛을 굴절시켜 필름이나 이미지 센서에 정확한 위치로 집중시키는 것이다. 이 과정을 통해 물체의 이미지가 필름에 형성된다.

• 모든 광선은 렌즈의 중심축(광축 또는 주축)에 평행하게 수렴한다.

  • 광축(렌즈의 중심축)에 평행하게 들어오는 모든 빛은 렌즈를 통과한 후, 렌즈의 중심에서 초점 거리 f만큼 떨어진 평면에 있는 한 점(초점)에 모인다.
  • 이 초점에서 빛이 모이기 때문에 이미지는 선명하게 보인다.

• 렌즈의 중심을 통과하는 광선은 굴절되지 않는다.

  • 렌즈의 중심을 통과하는 광선은 굴절되지 않고 그대로 직진한다. 렌즈가 왜곡 없이 이미지를 정확히 형성하도록 도와준다.

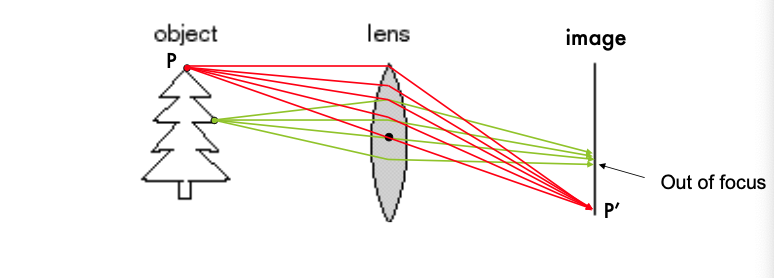
• "초점이 맞은 상태"

  • 렌즈는 물체에서 반사된 빛을 굴절시켜 필름이나 이미지 센서에 초점을 맞춘다. 이 과정에서 특정 거리(초점 거리)에 있는 물체는 선명하게 "in focus"로 나타난다.

• "초점이 맞는" 특정 거리가 있다.

  • 각 물체에는 렌즈의 초점 거리와 일치하는 특정 거리가 존재한다. 이 거리에 있는 물체만 선명하게 보이며, 이 거리보다 멀거나 가까운 물체는 흐릿하게 보일 수 있다.

• 심도(depth of field)와 관련이 있다.

  • 심도: 렌즈가 특정 초점 거리를 기준으로 물체를 선명하게 잡을 수 있는 범위
  • 심도가 깊을수록 더 넓은 범위의 물체가 선명하게 보이고, 심도가 얕을수록 특정 거리의 물체만 선명하게 보이며 나머지는 흐릿하게 보인다.

5. Lens Distortion

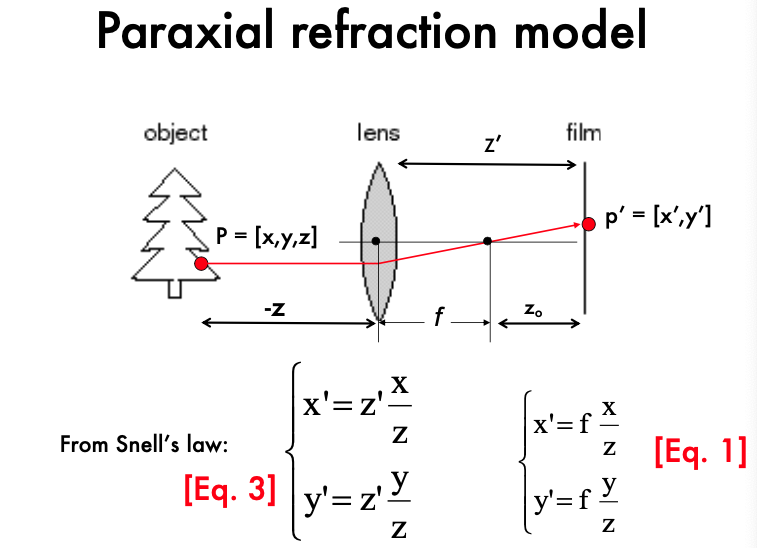
5.1 Paraxial Refraction Model (축소 굴절 모델)

1. 이미지 형성 원리:

   • 물체의 점 P(x, y, z)에서 나오는 빛은 렌즈를 통과하며 굴절되어 필름에 도달합니다.
   • 이 과정에서 빛은 렌즈를 지나면서 축소되어 초점 거리에 따라 특정 위치(P')에 이미지를 형성합니다.

2. 기하학적 관계식:

   • Snell의 법칙에 따라 물체의 좌표와 이미지 평면에 투영된 좌표 사이의 관계는 다음과 같은 수식으로 나타낼 수 있습니다:
     • $ x' = z' \frac{x}{z} $
     • $ y' = z' \frac{y}{z} $
   • 여기서, z'는 물체의 이미지가 형성되는 위치로, 물체의 실제 위치 z와 렌즈의 초점 거리 f에 의해 결정됩니다.

3. 초점 거리의 역할:

   • 초점 거리 f는 렌즈의 중심에서 필름까지의 거리로, 이 거리에 따라 빛이 모이는 위치가 결정됩니다.
   • 초점 거리가 짧을수록 빛이 더 빨리 모이고, 초점 거리가 길수록 빛이 멀리서 모입니다.

5.2 Radial Distortion (방사 왜곡)

1. 왜곡의 발생:

   • 렌즈를 통과하는 빛이 렌즈의 중심이 아닌 가장자리를 지나갈 때, 빛이 굴절되면서 이미지가 왜곡됩니다.
   • 이러한 왜곡은 물체의 실제 형태와 다른 형태로 이미지가 형성되는 결과를 초래할 수 있습니다.

2. 왜곡의 종류:

   • Pin Cushion 왜곡: 이미지가 내부로 오목하게 왜곡되는 현상으로, 중심부가 확대되고 가장자리가 축소됩니다.
   • Barrel 왜곡: 이미지가 외부로 볼록하게 왜곡되는 현상으로, 중심부가 축소되고 가장자리가 확대됩니다.

3. 방사 왜곡의 영향:

   • 렌즈의 왜곡은 이미지의 가장자리에서 가장 두드러지게 나타납니다.
   • 이러한 왜곡은 이미지의 품질에 영향을 미치며, 특히 건축 사진이나 정밀한 측정이 필요한 경우 문제가 될 수 있습니다.

6. Intrinsic and Extrinsic Parameters:

• Intrinsic Parameters(내부 파라미터)와 Extrinsic Parameters(외부 파라미터)의 개념을 소개하고, 카메라 모델에서 이들이 어떻게 사용되는지 설명
• Camera Matrix(카메라 매트릭스)의 구성과 역할

7. 3D Transformations:

• 3D 공간에서의 Translation(이동), Scaling(스케일링), Rotation(회전) 변환을 다루며, 이들이 카메라 모델에서 어떻게 사용되는지 설명
• Homogeneous Coordinates(동차 좌표)를 사용하여 이러한 변환을 표현하는 방법

8. Projective Transformations:
   • Projective Transformation(사영 변환)의 개념을 소개하고, 이 변환이 이미지에서 어떻게 적용되는지
   • 평행선이 이미지에서 Vanishing Point(소실점)에서 어떻게 만나게 되는지