지난 학기 학교 알고리즘 수업을 수강하며, 정리 해 놓았던 마크다운 문서입니다. 문제시 삭제하겠습니다
10. Dynamic Programming
- optimaization problem 해결 할수 있는 기법중 하나
- 한번 계산했던 sub problem 의 solution 다시 계산 x, solution은 table에 저장
- 똑같은 sub problem 만나면 table 값 이용해 문제 빠르게 해결
- 즉 메모리 더사용 중복된 계산 x, 문제 빠르게 해결
- Programming=table에 작성 의미, 주로 배열로 구현
- top-down 방법 (recursion) - 문제의 size가 n 일때 문제를 재귀를 통해 작은 문제를 만나는것, 더이상 풀수 없는 base case까지 가거나, 이미 해결한 sub problem을 만날때까지 쪼갠 다음 이전에 저장한 table 이용 sub problem 해결 (memoization 방법)
- bottom-up 방법 (loop) - base case부터 문제의 사이즈 증가시키면서 n이 될때까지 loop를 이용 문제 해결
Dynamic Programming version of a recursive algorithm
- sub problem의 solution을 저장 -> speed 개선 , space는 더 사용
- 기존에 계산 했던 solution 이전에 계산 했는지 안했는지 확인 -> dictionary=soln
- sol 저장 x -> 재귀 이용해서 계속 계산
- sol 저장 -> 저장된 내용 dictionary에서 찾아서 바로 활용 (재귀 이용 x)
- sol 리턴하기 직전에 soln에 저장 해줘야함
Ex : fib
fibDPwrap(n)
Dict soln = create(n); // 사이즈 n 테이블 생성
return fibDP(soln,n);
fibDP(soln,k)
int fib, f1, f2;
if (k < 2) fib = k; // base case
else if (member(soln,k-1) == false) //soln 에 sol저장 안되있으면
f1 = fibDP(soln,k-1); //재귀 통해 k-1 다시 실행
else f1 = retrieve(soln,k-1); // 계산 되있으면 단순히 테이블에서 읽어오기
if (member(soln,k-2) == false) f2 = fibDP(soln,k-2);
else f2 = retrieve(soln,k-2);
fib = f1 + f2;
store(soln,k,fib);
return fib;// bottom up은?
F0=0;
F1=1;
for i=2 to n
Fi=Fi-1+Fi-2;Matrix-Chain Multiplication
-
입력 : n개의 행렬 주어짐
-
결합 법칙 성립
-
어떤 순서로 곱하던 결과 값 같음, 곱셈 연산순서가 가장 적은 경우가 언제인지 찾는 문제
-
matrix Ai의 차원 pi-1 * pi 로 정의
-
두개의 행렬 곱할때 연산의 수 살펴보기 (p x q, q x r)
- pqr의 곱셈연산 필요(pr개의 원소들이 각각 q개의 곱셈 연산 필요)
- ex Ex) A1 = 30 × 1, A2 = 1 × 40, A3 = 40 × 10, A4 = 10 × 25
- ((A1 A2) A3 ) A4 : 30×1×40 + 30×40×10+ 30×10×25 = 20,700
- A1 (A2(A3 A4)) : 40×10×25 + 1×40×25+ 30×1×25 = 11,750
- (A1 A2) (A3 A4) : 30×1×40 + 40×10×25+ 30×40×25 = 41,200
- A1 (( A2 A3 ) A4) : 1×40×10 + 1×10×25+ 30×1×25 = 1,400
- A1 (( A2 A3 ) A4) : optimal solution
- 1400: optimal solution의 value
Development
- optimal solution 구조를 먼저 파악하기
- 구조 파악했다면 값 계산하도록 recursive하게 정의 (점화식 정의 단계)
- 점화식 이용하여 optimal solution의 value값 계산
- optimal solution의 "과정"계산 (optional step)
Step 1: The structure of an Optimal Parenthesization
- AiAi+1…Aj의 행렬 나열을 Ai…Ak, Ak+1…Aj 두개의 sub problem으로 쪼갬 (i ≤ k < j)
- Cost = (cost of computing Ai..k) + (cost of computing Ak+1..j) + (cost of multiplying them)
- 이 문제를 정확하게 계산하기 위해서 모든 가능한 위치=k에 대해 다 계산을 해보고 그중에 비용이 최소인 것을 찾아야함
Step 2: A Recursive Solution
- 두개의 table 필요
- m[i,j] : Ai...j까지 행렬 곱셈할때 필요한 최소 횟수를 저장 할 table
- s[i,j] : 최소횟수를 계산 했을때 그 때 쪼개는 k값을 저장하는 table (step 4 계산위한 테이블)
- 0 if i=j (size 1 의미=base case)
- min {m[i,k] + m[k+1,j] + pi-1pkpj
} if i < j (size 2 이상)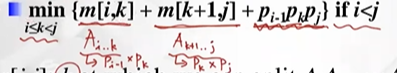
Step 3: Computing the Optimal Costs
top-down 대신 bottom-up 이용 계산
-
Ex) A1 = 30 × 1, A2 = 1 × 40, A3 = 40 × 10, A4 = 10 × 25
-
𝒑𝟎 = 𝟑𝟎, 𝒑𝟏 =1, 𝒑𝟐 = 𝟒𝟎, 𝒑𝟑 = 𝟏𝟎, 𝒑𝟒 =25.
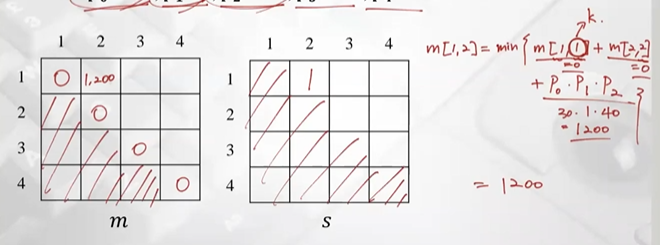
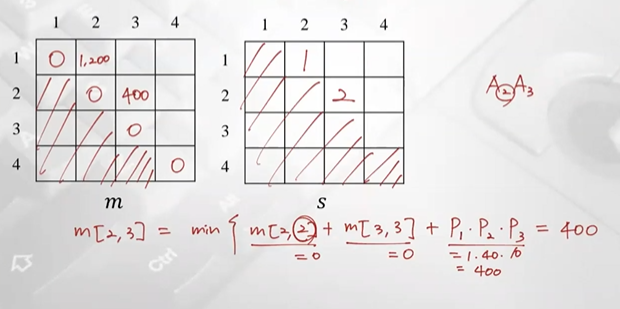
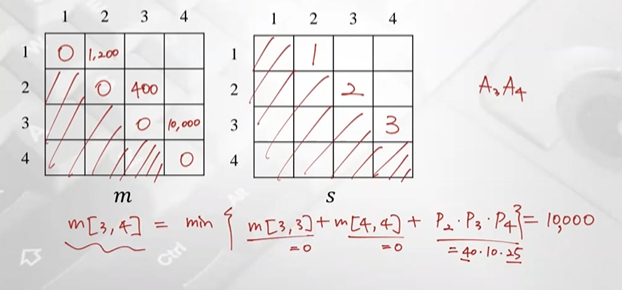
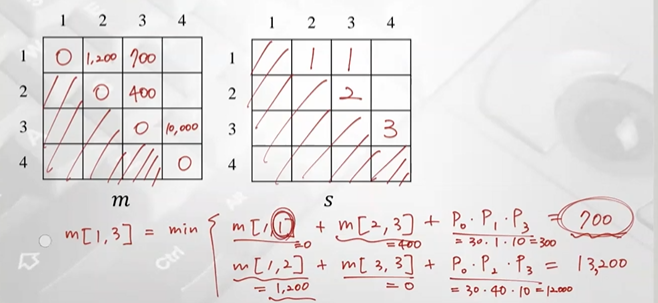
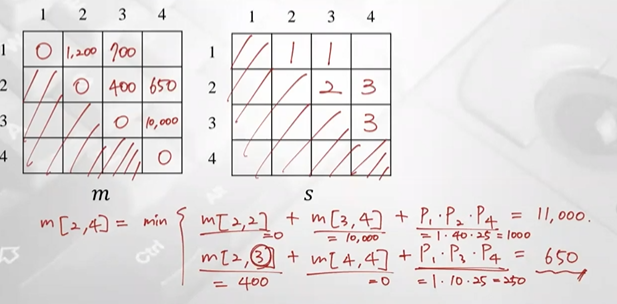
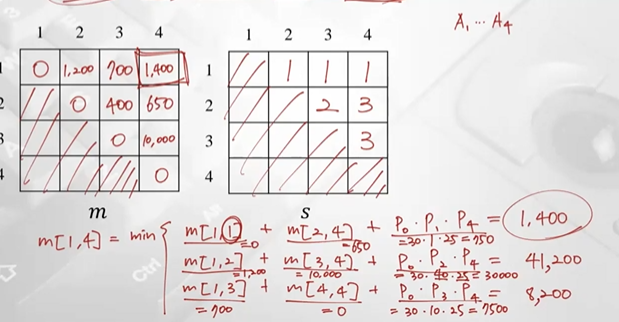
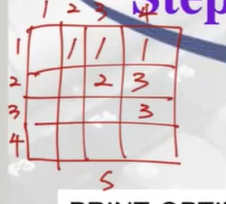
m, s table 계산 완료, 최종적으로 마지막 값 1400이 optimal solution의 value (A1부터 A4까지 필요한 곱셈연산의 최소 횟수)
-
Step 4: Constructing an Optimal Solution
PRINT-OPTIMAL-PARENS(𝑠, 𝑖,𝑗) //i=1, j=4
1 if 𝑖 = 𝑗
2 then print “A”i //base case
3 else print “(”
4 PRINT-OPTIMAL-PARENS(𝑠, 𝑖, 𝑠[𝑖,𝑗]) //s[i,j]에는 k값 저장 (Ai..Ak) -> left child
5 PRINT-OPTIMAL-PARENS(𝑠, 𝑠[𝑖,𝑗]+1, 𝑗) //s[i,j]+1=k+1 (Ak+1...Aj) -> right child
6 print “)recursion tree로 표현 가능
-
초기값 s[1,4]에 대한 k 값=1
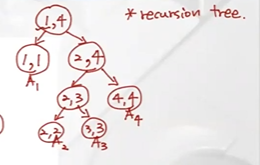
-
(1,4)의 left child는 i,k로 나타낼수 있으므로 (1, 1)
-
right child는 k+1, j 로 나타낼수 있으므로 (2,4)
-
위와 같은 방식으로 트리 만들 수 있음
-
왼쪽 자식 호출되기전 "(" 출력
-
오른쪽 자식이 호출되고 난후 직후 돌아올때 ")" 출력
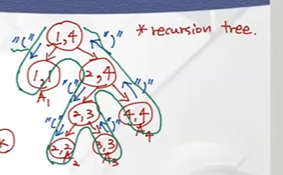 in order 순회 방식으로 출력
in order 순회 방식으로 출력
-> (A1((A2A3)A4)) 곱셈 순서 출력 가능!!
분석
Step 3 : matrix chain 길이 1 일때 계산, 2일때 계산, 3일때 계산,,,, n일때까지 계산 -> n+(n-1)+...+1 = O(n^2)의 셀 존재
하나의 셀 계산하는데 o(n) time 걸림
따라서 O(n^3) time, O(n^2) space
Step 4 : recursion tree노드 개수 분석
n개의 leaf 존재, n-1개의 internal node가짐 -> 총 2n-1개의 노드 가짐 따라서 O(n) time 에 수행가능
O(n^2) space (s 테이블을 계속 사용하기 때문)
