4. Red Black Tree

glow.soon·2022년 1월 19일

알고리즘

목록 보기

5/12

지난 학기 학교 알고리즘 수업을 수강하며, 정리 해 놓았던 마크다운 문서입니다. 문제시 삭제하겠습니다

Binary Search Trees

노드의 key들이 어떤 순서조건 만족시켜 줘야함 (binary search tree property)

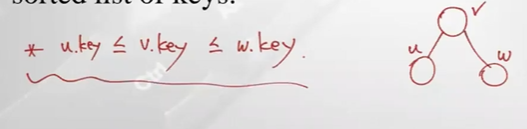이런 순서 조건 만족시켜줘야한다

inorder 순회하면 오름차순한 결과 얻을수 있다

Binary Search Tree Retrieval

Element bstSearch(BinTree bst, Key K)
Element found
if (bst == nil) // base case
    found = null;
else
    Element root = root(bst);
    if (K == root.key)
        found = root;
    else if (K < root.key)
        found = bstSearch (leftSubtree(bst), K);
    else // K > root.key
        found = bstSearch(rightSubtree(bst), K);
return found;

수행시간 트리모양 어떤가에 따라 다름

n개의 노드가 저장되어있는 binary tree

한쪽으로 쭉 늘어진 형태 ,탐색 최악시간 : θ(n)
트리가 가능한 balanced인 상태 , θ(logn)

목표->binary tree를 최대한 balanced하게 만들기 -> red black tree로 가능

Red-Black tree

다음의 조건 만족하는 binary search tree

Root property: root노드는 무조건 black
External property: 모든 leaf노드는 black
internal property: red노드의 children은 다 black이다
depth property: 모든 leaf노드들은 같은 black depth를 가진다

(black edge: black 노드에서 parent노드로 향하는 edge->

black depth: 해당 노드에서 root까지의 black edge수)

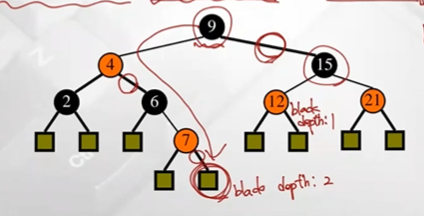RB tree의 예

Height of Red-Black tree

레드 블랙트리는 height O(logn)

어떤 레드 블랙트리가 있으면 어떤 depth는 비교적 짧고 어떤 depth는 비교적 길것임

red node의 children은 무조건 블랙이어야 함으로
가장 긴 겨우는 b,r,b,r,b,r,...b인 경우일것임

가장 짧은 경우는 black노드만 있는경우, 이 둘의 root까지 가면서 만나는 black노드의 개수는 같을 것이다

이둘의 높이차는 최대로 2배차이밖에 나지않는다

h<=2logn => θ(logn), 따라서 탐색의 수행시간 O(logn) time

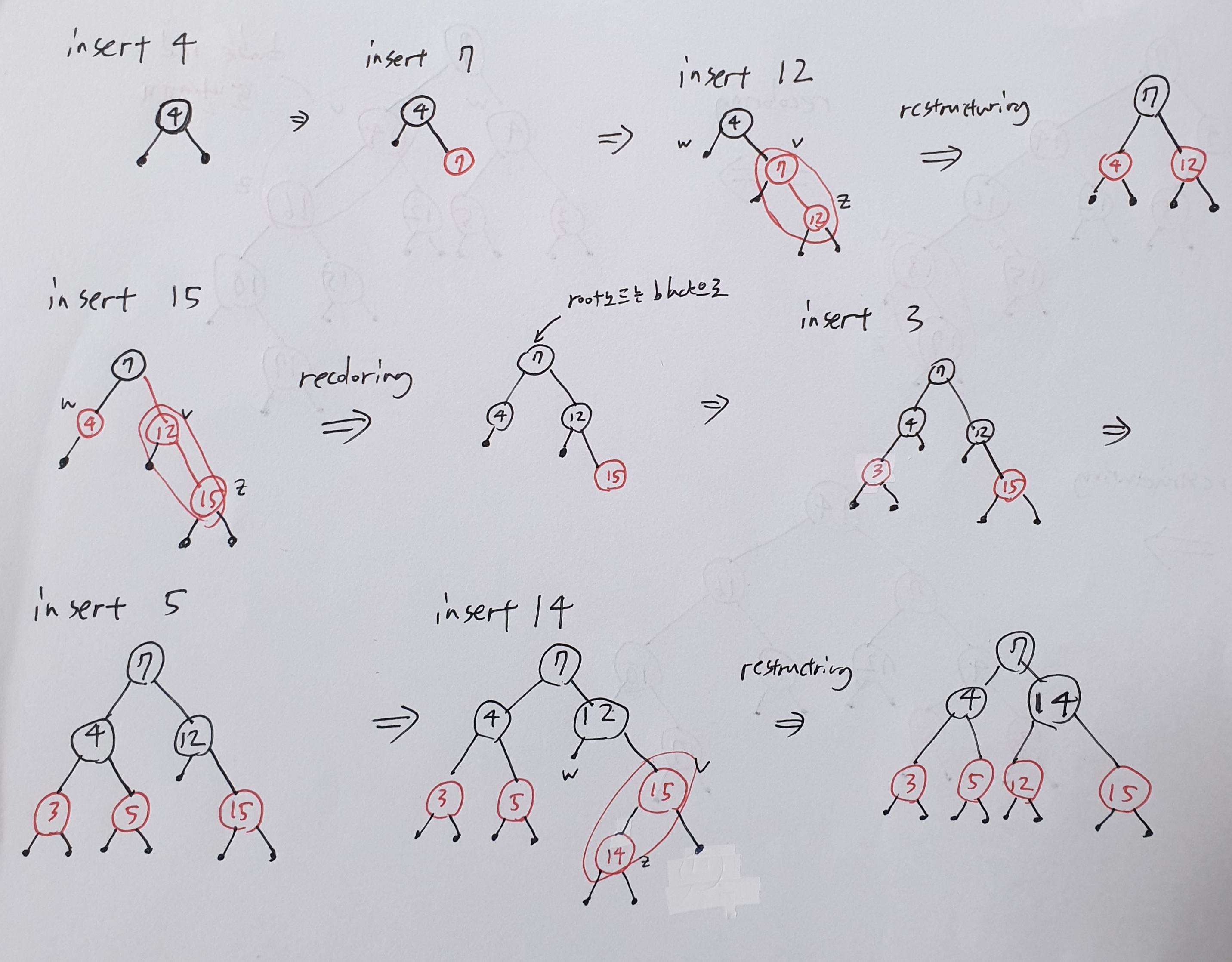
Insertion

BST의 삽입연산과 유사

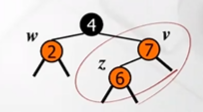
key값 4를 삽인한다고 하자(삽입 key는 무조건 red node)

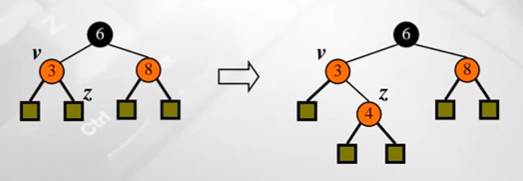
double red 상황 발생, 어떻게 해결할까?

삽입한 노드=z, z의 부모노드=v, v의 형제노드를 w라 하자

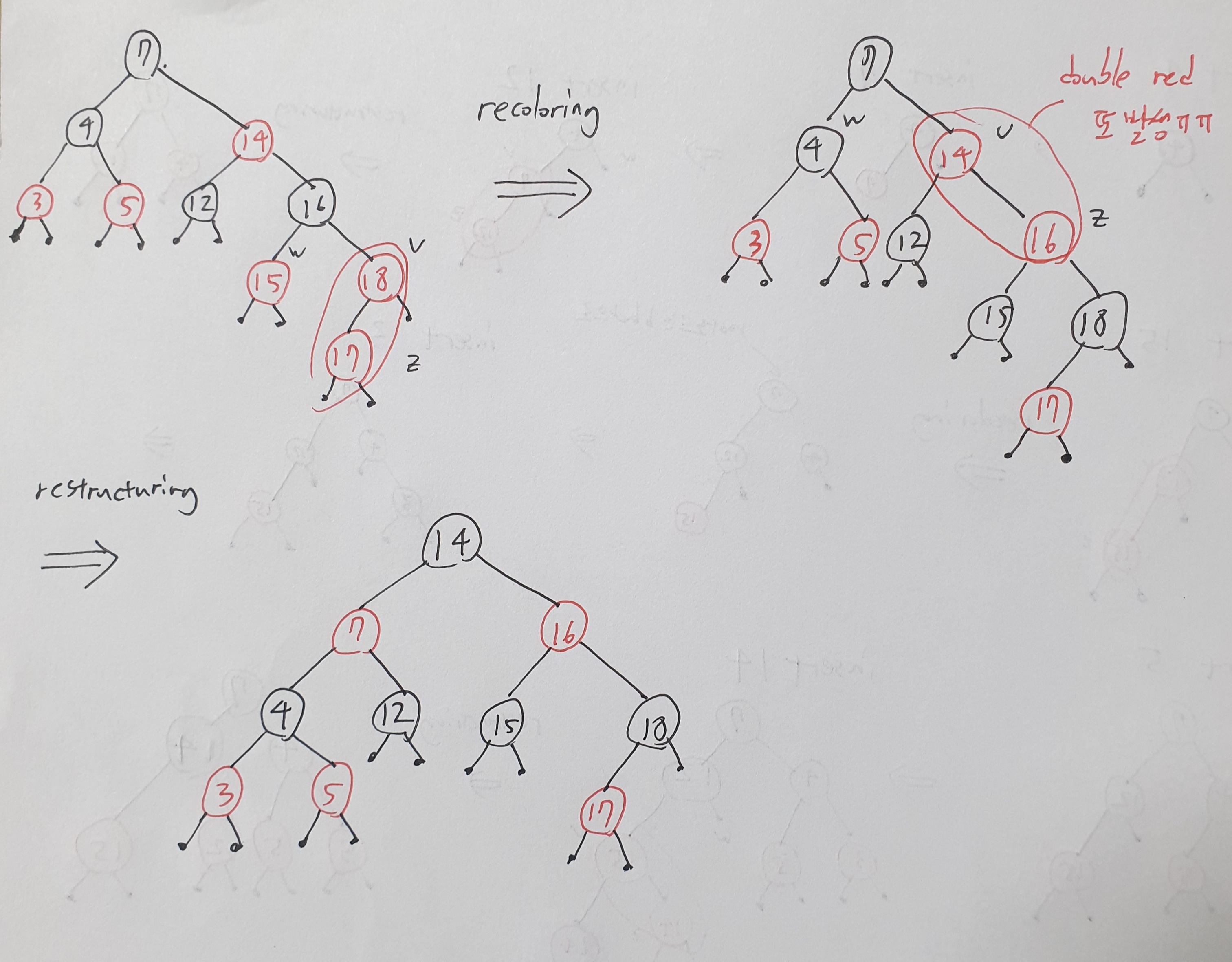
Restructuring

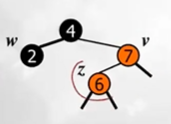w가 black인 경우 restructuring해줘야함

z와 v 그리고 v의 부모노드에 주목하자

키값이 중간인 노드를 부모로 나머지 노드를 자식노드로 처리해준다
root노드는 black노드로, 자식들은 red 노드로 처리

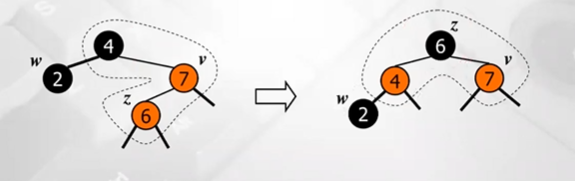
자체 시간 복잡도 O(1), 총수행시간은 삽입한뒤 일어나므로 O(logn)

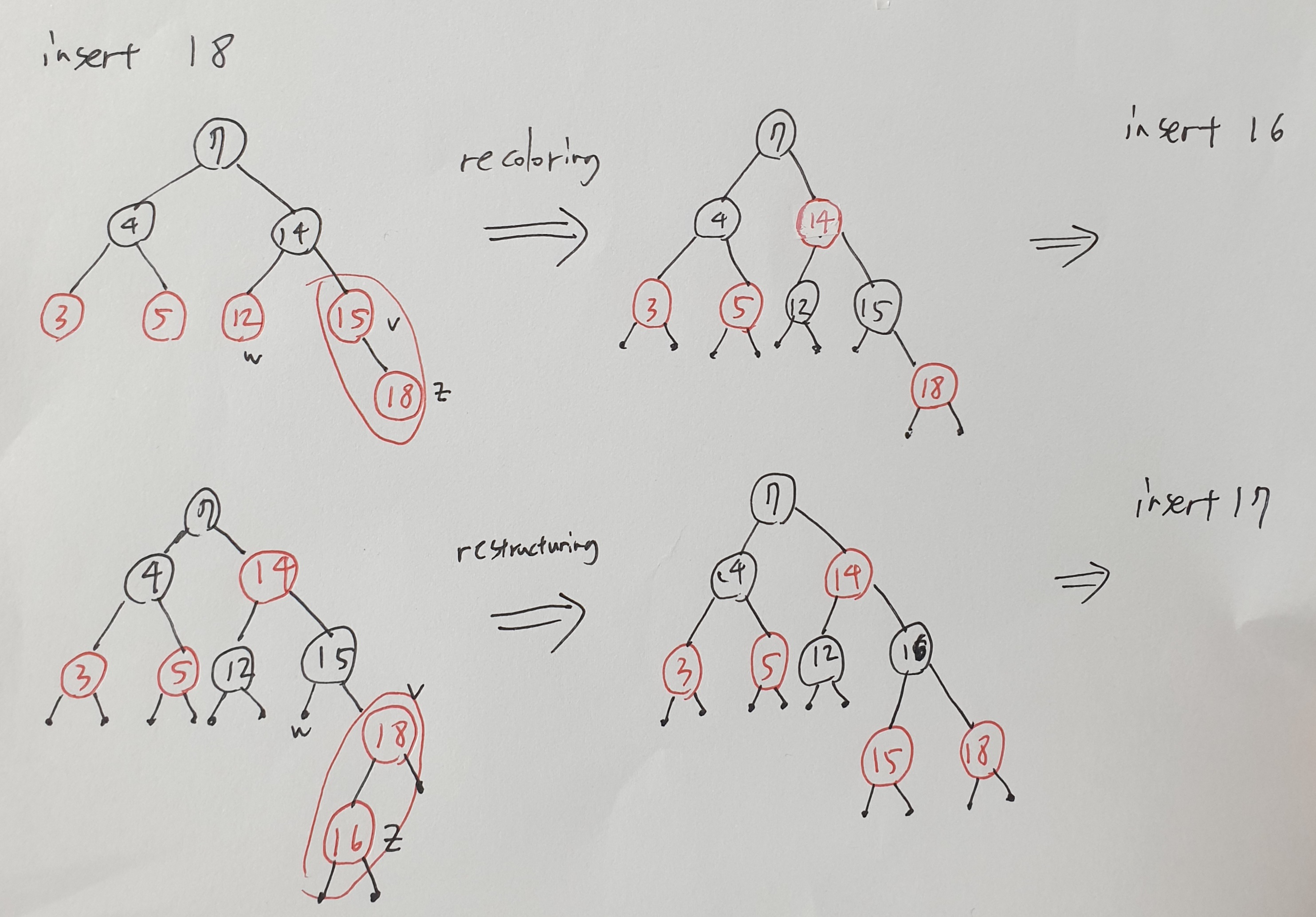
Recoloring

w가 red인 경우 recoloring 해줘야함

w, v를 black노드로 바꾸고 그 부모노드를 red로만 바꿔주기

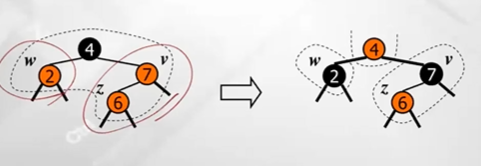
but, recoloring은 double red문제 또 발생할 수있다

자체 시간복잡도 O(1), 최악의 경우 leaf부터 root까지 가능: O(logn)

Algorithm insertItem(k, o)
1. We search for key k to locate the
insertion node z // O(logn) time

2. We add the new item (k, o) at
node z and color z red // O(1) time

3. while doubleRed(z)
    if isBlack(sibling(parent(z)))
        z <- restructure(z) // O(1) time
        return
    else { sibling(parent(z) is red }
        z <- recolor(z) // O(logn) time