지난 학기 학교 알고리즘 수업을 수강하며, 정리 해 놓았던 마크다운 문서입니다. 문제시 삭제하겠습니다
Traversing Graphs
Breadth-first search (BFS) and depth-first search (DFS)
정확히 한번 각각의 정점과 간선 방문하는 알고리즘 (O(n+m) time)
- vertex 상태
- undiscovered
- discovered
- finished
- edge 상태
- unexplored
- explored
Depth first search for Digraph
- 시작 정점 고름, d=0
- 방문할수있는 정점있으면 계속 방문 (d+1)
- 더이상 방문할수있는 정점 없으면 finish
- backtrack
- 모든 정점 방문했으면 종료
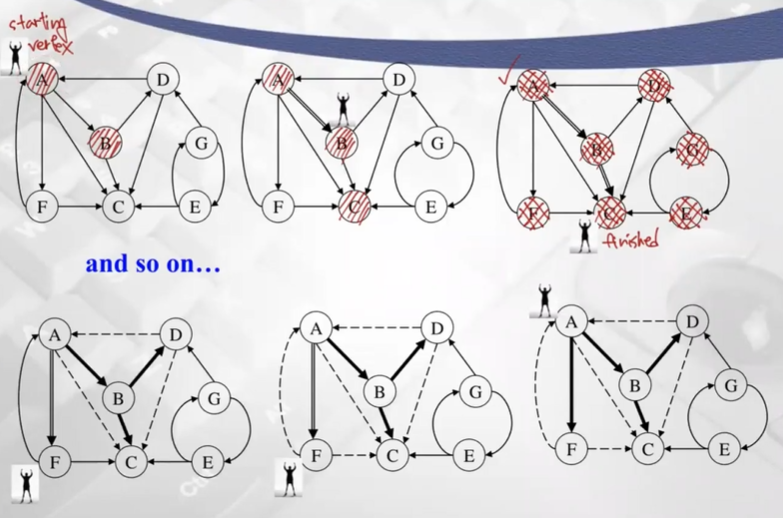
- visited 되는 순서: A, B, C, D, F, E, G
- finished 되는 순서: C, D, B, F, A, G, E
Breadth-first Search for Digraph
- 임의의 정점 선택, d=0으로 초기화
(다른 정점까지 최단거리, 경로 계산 가능) - d=1 정점 다찾고, d=2 정점 다찾기 ....-> 영역 넓히듯이 탐색
BFS example
가정 : 방문할수있는 여러개 정점 있는경우 알파벳 작은거 부터 방문
- starting 정점 : A (BFS는 하나의 큐 필요)
- A 큐에 삽입, d=0으로
- A를 dequeue, A에서 갈수 있는 정점 탐색
- B,C,F 삽입 (d=1)
- B dequeue, B에서 갈수있는 정점 탐색 (c는 이미 discovered, D 삽입(d=2))
- C, F dequeue
- D dequeue
- 더 이상 갈수있는 곳 x, d=0으로 초기화 starting 정점 E 추가
- E dequeue, G 삽입(d=1), G dequeue
->모든 정점 엣지 한번씩 순회 가능
최단 경로, 최단 거리를 구하려면 E,G 부분에서 d=무한대 로 저장하도록 계산
또한 각 노드에서 나를 탐색하게 한 정점에대한 정보 저장 할 것 필요-> predecessor(parent)
index D 에는 B 저장
A부터 D까지의 최단 경로는? D부터 역순으로 출력해주기 P[D]=B, P[B]=A, 스택 같은거에 삽입 ->A,B,D -> pop -> 최단경로 A,B,D
O(n+m) time 에 수행가능
Strongly Connected Components (SCC)
임의의 digraph D에서 SCC 찾기
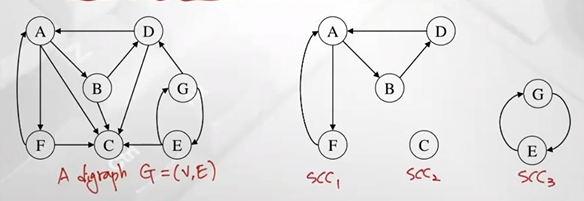어디에 적용? 사람들 팔로우 관계성(sns)
코사라주 알고리즘
2번의 dfs 이용
phase 1
- 입력으로 주어진 G에 대해 DFS 적용
- finishing time에 스택에 정점 삽입
(finish stack)
phase 2
- transpose graph G^T생성 (원래 그래프 엣지 방향 반대로)
- G^T에 대해 두번째 DFS 수행
- 처음 발견되는 starting 정점에 대해 leader라고 부를 것
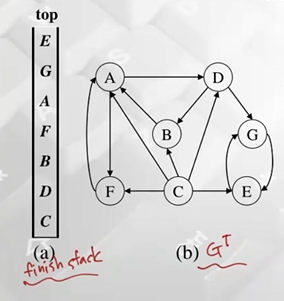phase 2 DFS 하기전까지 수행한 것, 그다음
-
SCC 정보 저장할 array 생성
-
finish stack에서 pop 해서 나온 E를 reader로 설정
-
E부터 dfs 수행, 결과 array에 저장
-
reader A
-
reader C
위 과정을 완료하면 SCC 찾기 가능 (같은 리더 가진 경우 같은 SCC) SCC개수=리더의 수
분석
phase 1: O(n+m) time
phase 2 : transpose graph 생성 -> O(n+m) time, 2nd DFS : O(n+m) time
total : O(n+m) time
