지난 학기 학교 알고리즘 수업을 수강하며, 정리 해 놓았던 마크다운 문서입니다. 문제시 삭제하겠습니다
problem: single source shortest paths
source: starting 정점 주어짐
source부터 reachable한 모든 shortest path찾는 문제
(이 교재에선 single source는 source, destination 모두 주어진거 말함)
- single-source shortest paths : 입력으로 source 정점 주어짐
- single-pair shortest paths: 입력으로 source와 destination 주어짐
- single-destination shortest paths: destination만 주어짐
- all-pairs shortest paths: 입력으로 주어진 모든 정점쌍에 대한 shortest path 구하기
shortest path property
- x부터 z까지의 shortest path있다고 가정
- 중간에 y 정점있다
- 이 shortest path는 x부터 y의 P와 y부터 z까지의 Q로 구성되있다 하겠음
- then, P도 shortest path이고 Q도 shortest path이다 (optimal substructure)
but, 이 역은 성립하지 않음. 예를 들어 x는 인천, y는 부산, z는 서울이라 할때 인천에서 부산까지 shortest path P, 부산에서 서울까지 shortest path Q있다. 이 두 shortest path를 합친다해도 인천에서 서울까지의 shortest path라 할 수 없음.
Dijkstra's shortest path algorithm
조건: weight가 음수가 되면 안됨
Prim 알고리즘과 거의 유사하게 동작
dijkstraSSSP(G,n) // OUTLINE
Initialize all vertices as unseen.
Start the tree with the specified source vertex s; reclassify it as tree; //root
define d(s,s) = 0. //자기자신 distance 0으로 초기화
Reclassify all vertices adjacent to s as fringe. // s와 인접한 모든 정점들 fringe상태로 업데이트
-------------------초기화 단계
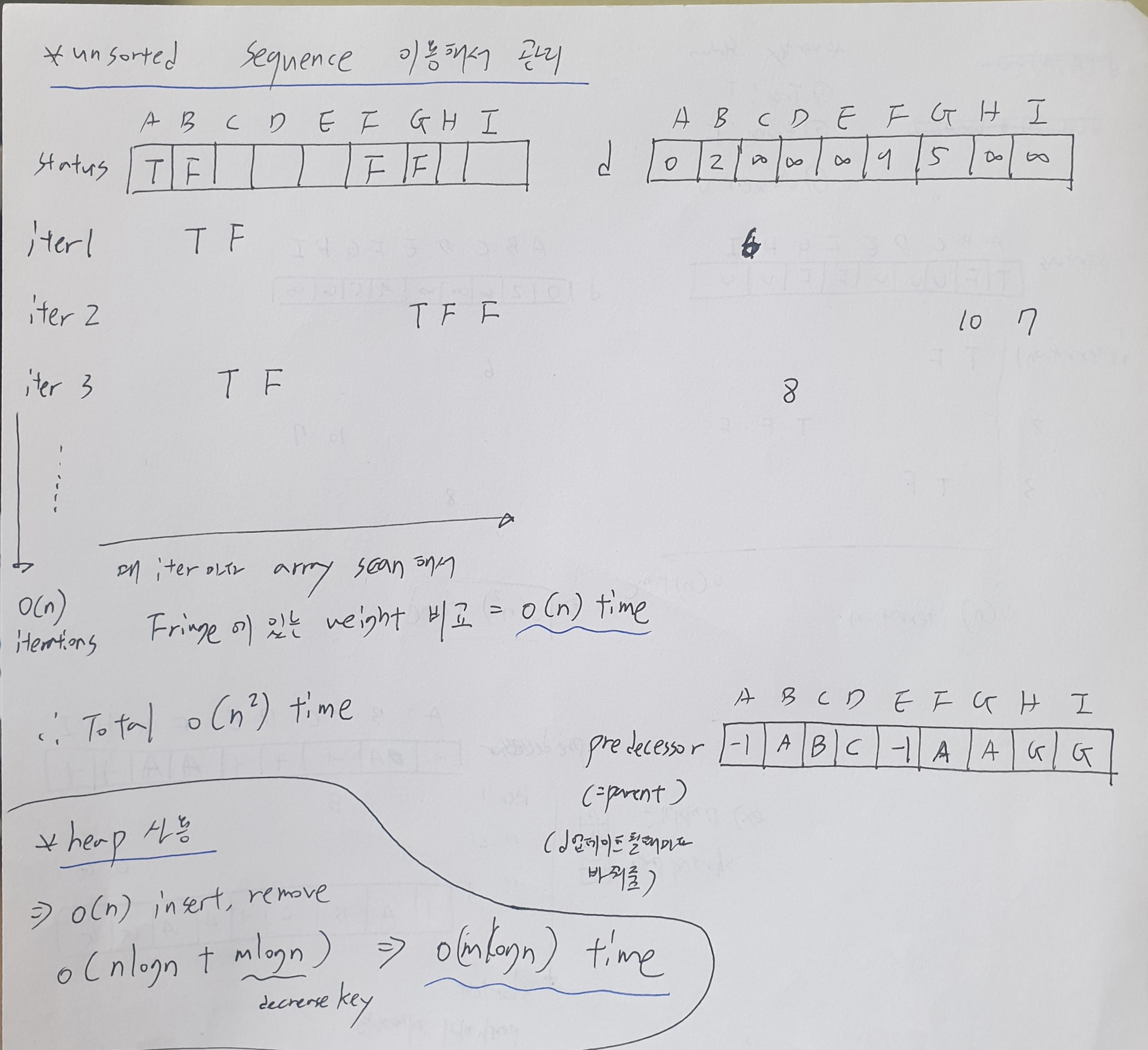
while there are fringe vertices: // 우선순위 큐로 구현 (unsorted sequence(O(N^2))) or heap(O(mlogn)))
Select an edge between a tree vertex t and a fringe vertex v
such that (d(s,t)+W(tv)) is minimum; //s부터 t까지의 거리+tv거리
Reclassify v as tree; add edge tv to the tree;
define d(s,v) = (d(s,t)+W(tv)). // 제일 작은 path선택
Reclassify all unseen vertices adjacent to v as fringe.Example
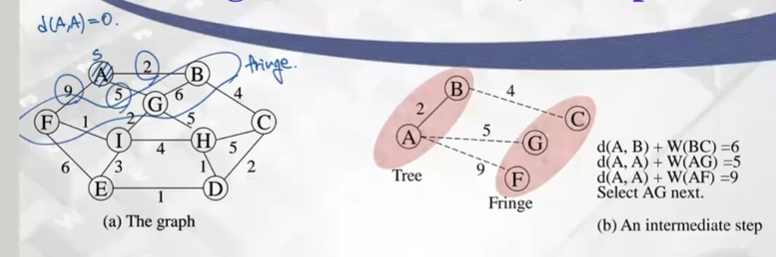
-
시작 정점 A
-
가장 작은 weight 가진 B를 Tree상태로 업데이트
-
B에서 인접한 A, G, C 체크
-
G는 기존에 A에서 G로 가는 weight가 더 작기때문에 그대로, C는 unseen 상태였기 떄문에 fringe 상태로 업데이트
-
Tn까지 수행하고, 이 때의 상태가 A로부터 다른 모든 정점까지의 shortest path 계산한것
Unsorted sequence 이용
weight 음수 안되는 이유

다익스트라 알고리즘은 한번 계산되면(d(A,B)=2) shortest path fix되기 때문에 음의 edge가 존재하면 이런 경우 발생가능
9. Transitive Closure, All-pairs Shortest paths
Floyd-warshall's algorithm 이용 그래프의 Transitive Closure 찾기
Transitive Closure
digraph G가 주어졌을때 G*는 G와 같은 정점 정보 가짐 대신 edge 정보 추가
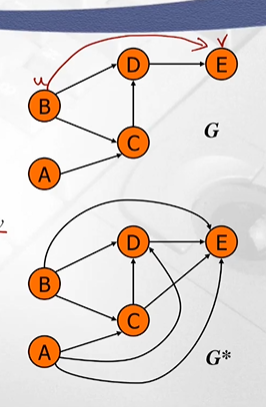 ex) B에서 E path 존재하면 B에서 E로 한번에 가는 directly connected edge 추가해주기
ex) B에서 E path 존재하면 B에서 E로 한번에 가는 directly connected edge 추가해주기
모든 이런 path에 대해 다 추가해준것이 G의 Transitive closure G*
Transitive closure는 n번의 dfs로도 가능 => O(n(n+m)), 만약 m이 O(n^2)에 바운드된다면 이때 수행시간은 O(n^3)이 됨
Floyd-warshall Transitive Closure
- 모든 정점에 대해 번호를 매겨줌
- 번호매긴 정점을 이용해서 바로 연결할수있는 edge 만들기
Algorithm FloydWarshall(G)
Input digraph G
Output transitive closure G* of G
i <- 1
for all v bound G.vertices()
denote v as vi
i <- i + 1
G0 <- G
for k <- 1 to n do
Gk <- Gk - 1
for i <- 1 to n (i != k) do
for j <- 1 to n (j != i, k) do
if Gk - 1.areAdjacent(vi
, vk) and Gk - 1.areAdjacent(vk, vj)
if not Gk.areAdjacent(vi, vj)
Gk.insertDirectedEdge(vi, vj , k)
return Gn어떤 step Gk에 대한 계산 하기위해 기존에 계산된 Gk-1로부터 계산 : 다이나믹 프로그래밍 기법 활용
adjacency matrix 활용했을때 O(n^3) time, when areAdjacent is O(1)
Example
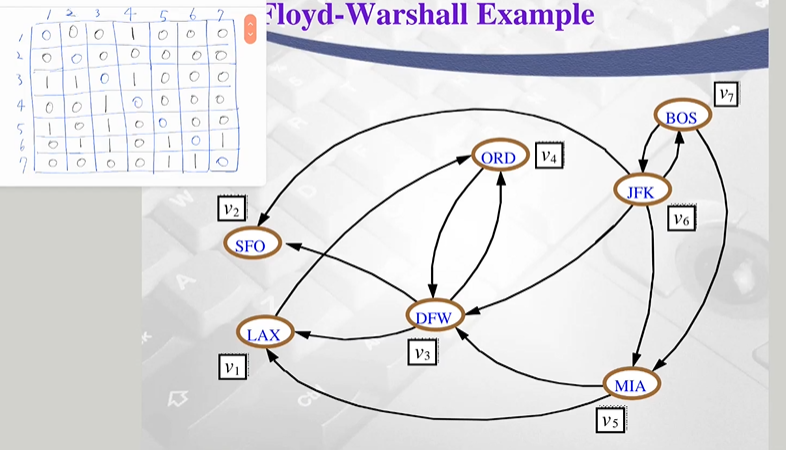
- 각 정점에 대해 outgoing 엣지 유무 1로 업데이트 (input G)
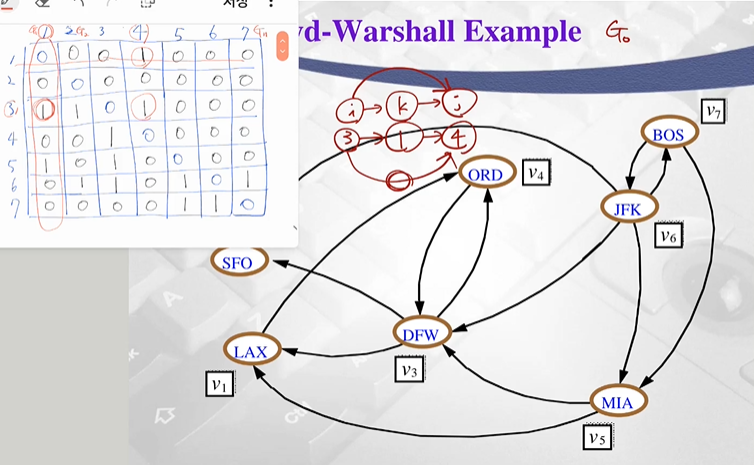
- column을 위에서 아래로 스캔
- edge 3에서 존재, (3,1) 이라고 볼수 있음
- 1번 row를 스캔
- (1,4) edge 존재
- (3,1)->(1.4) = (3,4)
- 이미 기존에 (3,4)에 edge 존재 -> pass
- 이런 단계로 알고리즘 진행
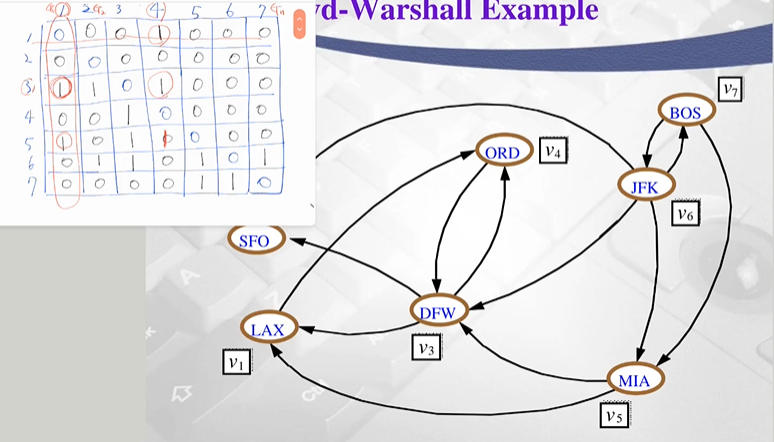
- (5,1) edge 존재
- 1 row 확인
- (1,4) edge 존재
- (5, 1) -> (1, 4) = (5,4)
- (5,4)에 1 업데이트
- phase 1 끝
Phase 2
- 2 row 에 존재 edge 없음, 종료
Phase 3
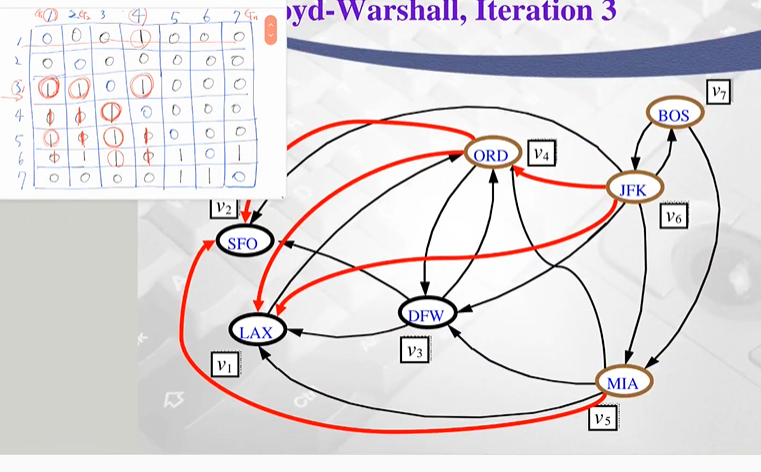
-
(4,3) 존재
-
3 row 확인
-
(3,1), (3,2) (3,4) 존재
-
(4,1) (4,2)에 1 업데이트 ((4,4) 자기자신은 제외)
-
(5,3) 존재
-
3 row 확인
-
(3,1), (3,2) (3,4) 존재
-
(5,1), (5,2), (5,4) 1 업데이트
-
(6,3) 존재
-
3 row 확인
-
(3,1), (3,2) (3,4) 존재
-
(6,1), (6,4) 1 업데이트
.
.
.
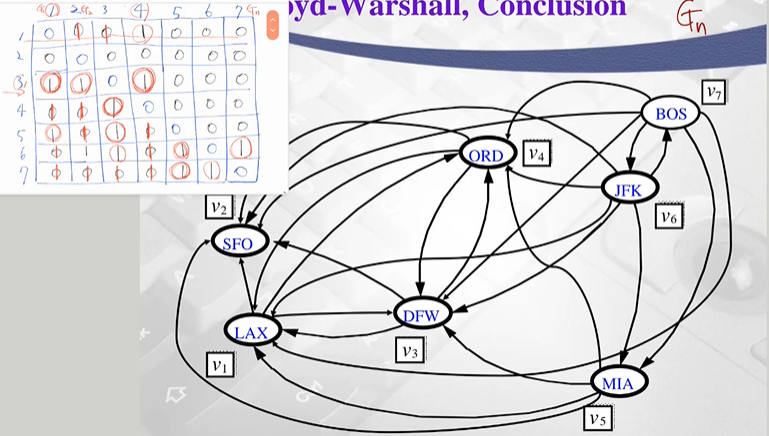 최종 결과 Gn=G*
최종 결과 Gn=G*
All-pairs shortest path
앞선 알고리즘 좀만 변경하면 all-pairs shortest path 찾을 수 있음 (모든 정점 쌍에대한 shortest distance 찾기)
- n번의 다익스트라 알고리즘 사용하면 찾을수 있음
- O(nmlogn) time 소요 (힙이용 다익스트라 O(mlogn))
- m -> O(n^2)이면 O(n^3logn)에도 수행 = O(n^3)
example
- phase 1
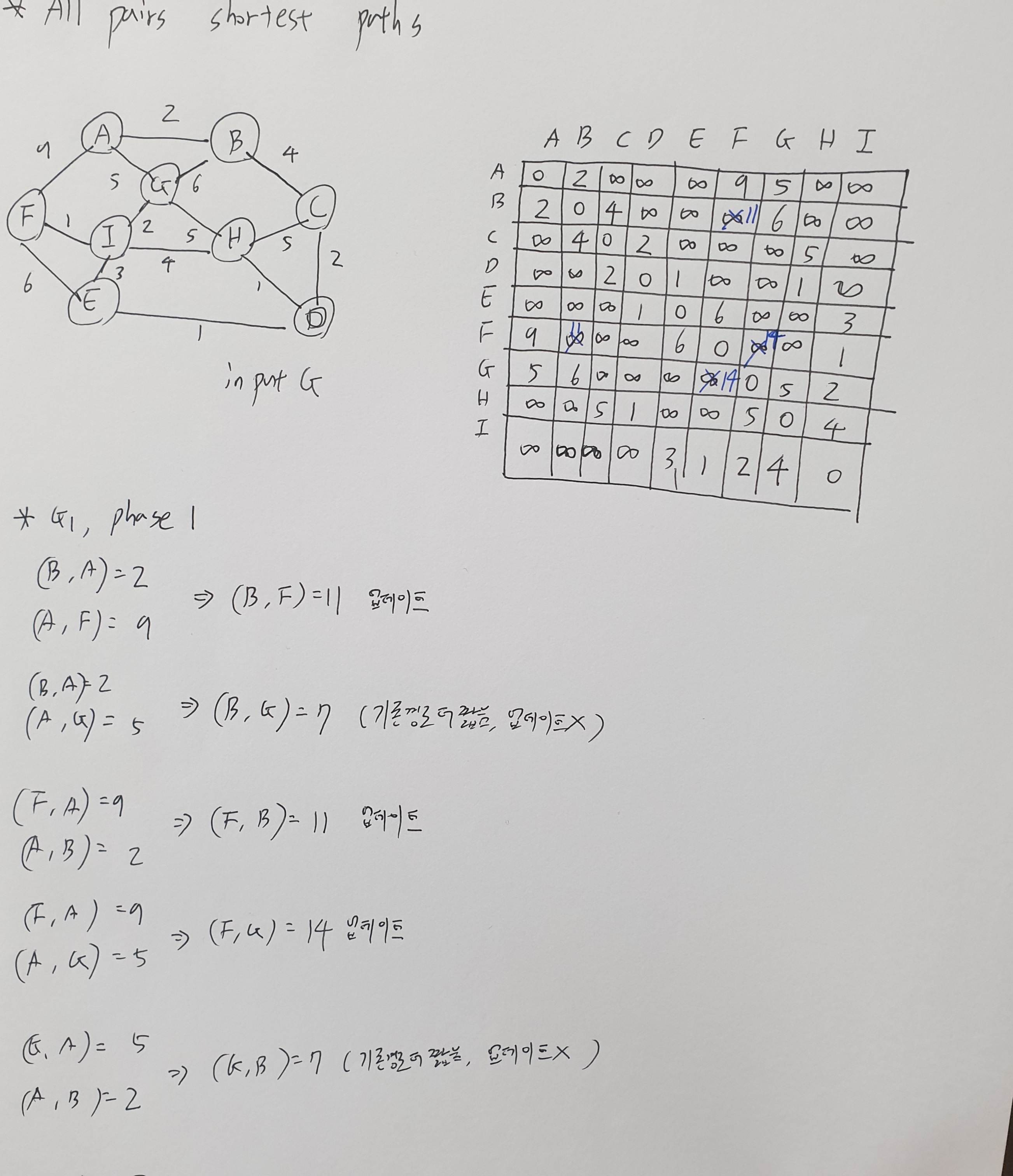
- phase 2
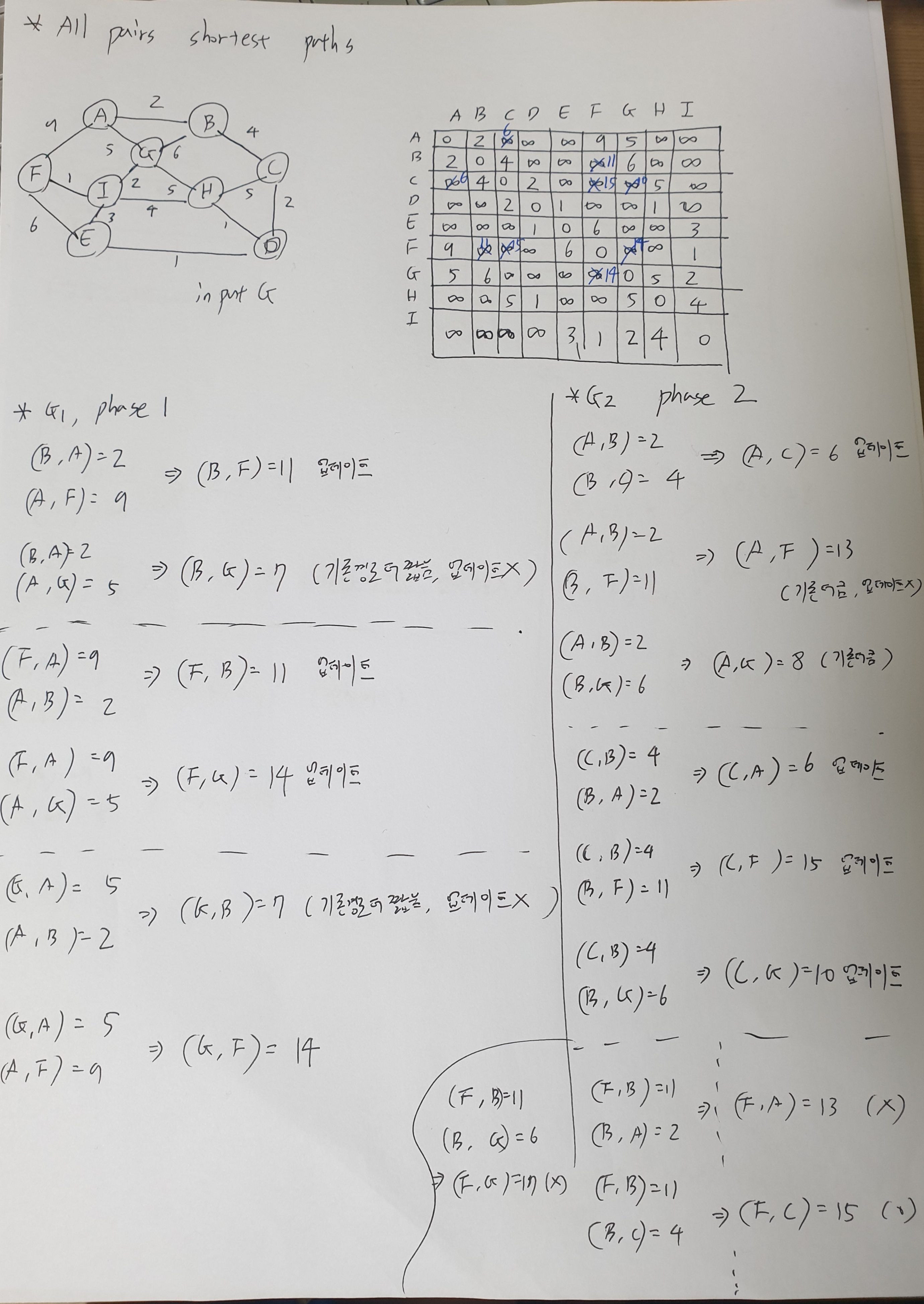
이런 방식으로 알고리즘 수행
분석 : n phases-> O(n) time
scan 하는데 O(N) * O(N)=> O(N^3)에 수행가능
