1. The Problem of Overfitting

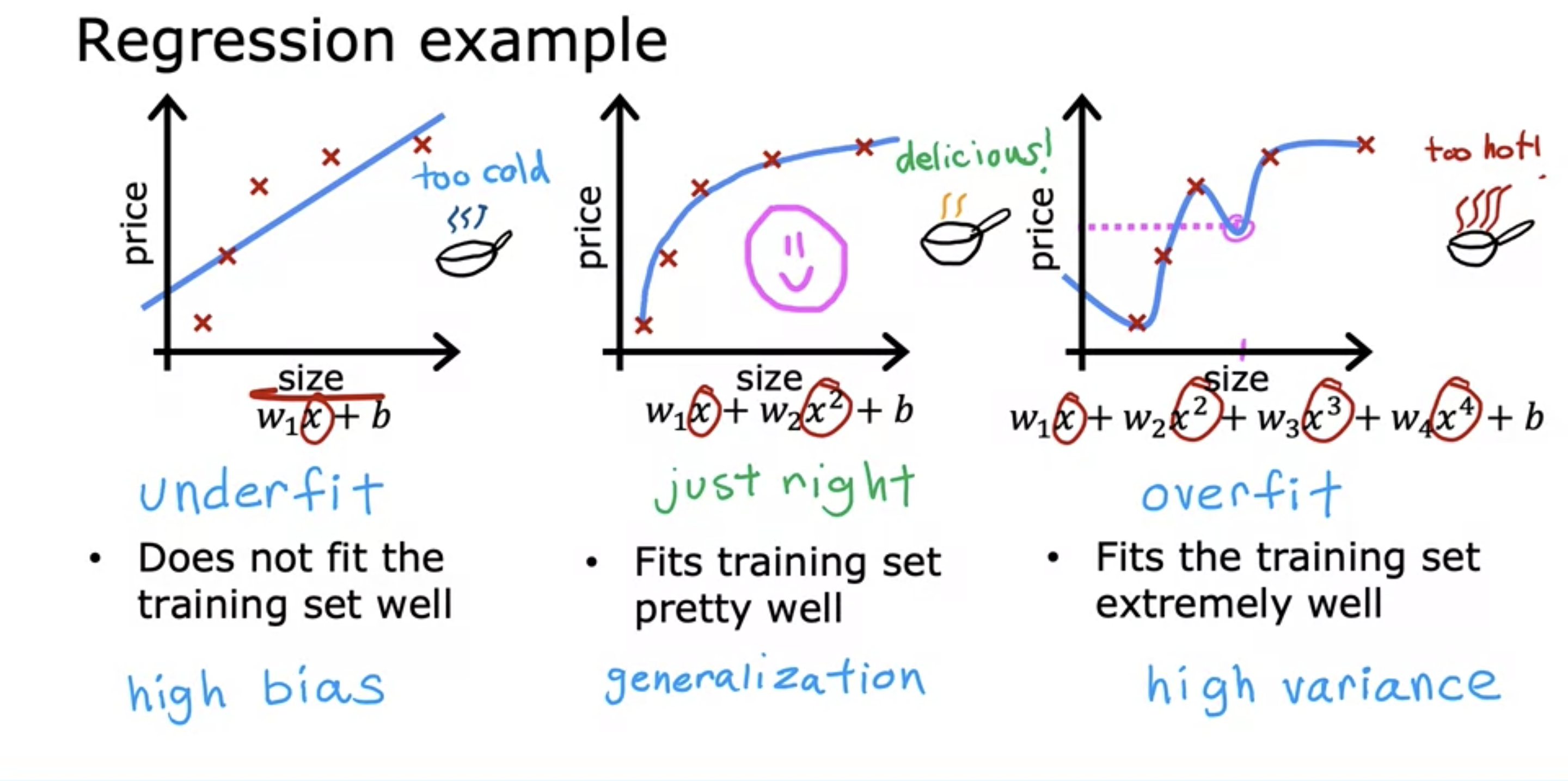
• Underfit is when the model we came up with does not fit the data accurately because the model has high bias for certain model.
  • Example above shows the model having high bias for a linear model, when quadratic model can fit it better.
• Generalization is when the model is able to generalize the pattern for new training data as well.
• Overfit is when the model fits the training data too well that it cannot predict the new training data accurately.
  • It has high variance meaning that the graph can look wiggly to fit the existing data.

2. Addressing Overfitting

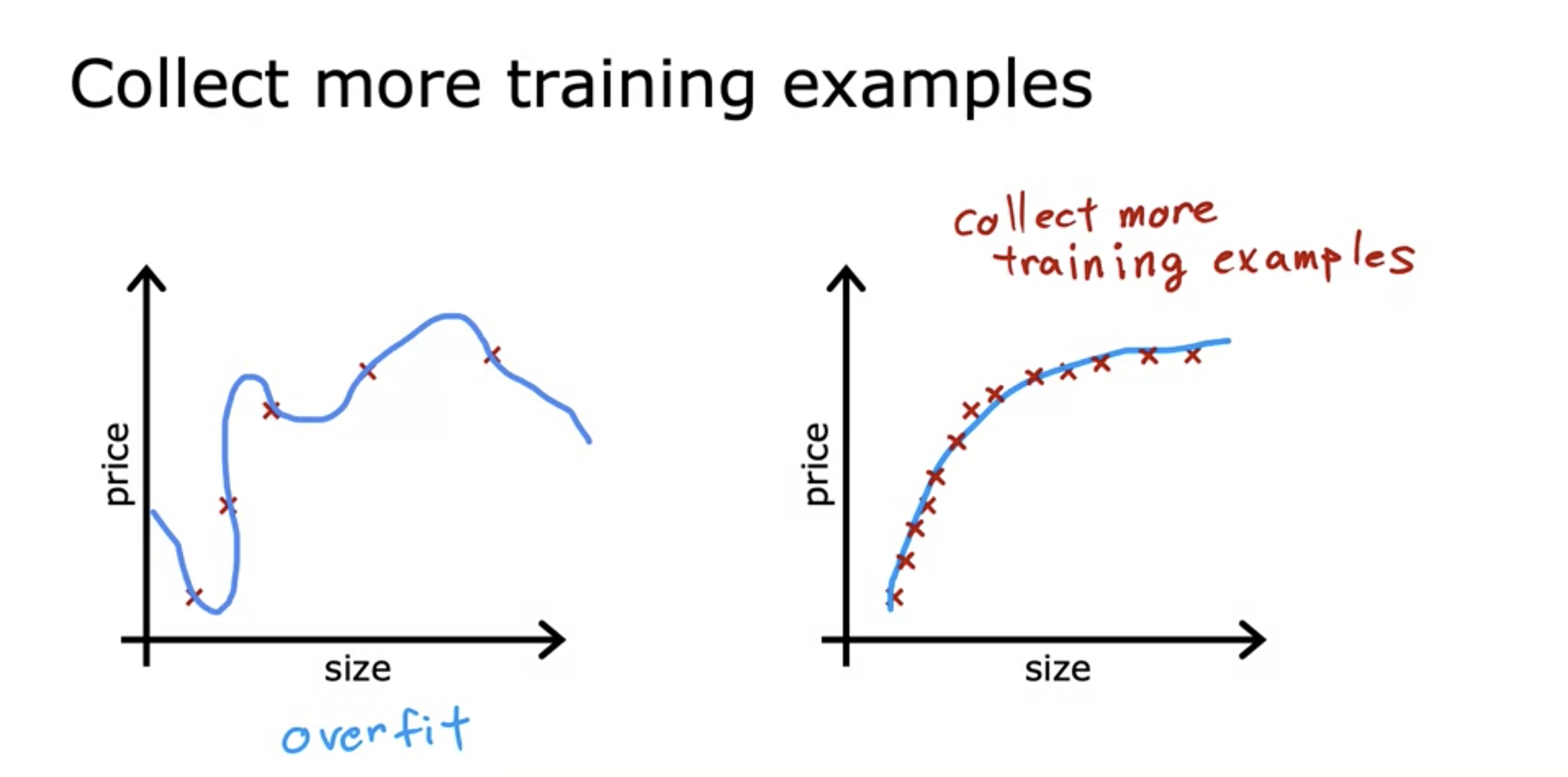
1. Collecting more training examples

2. Include / exclude features

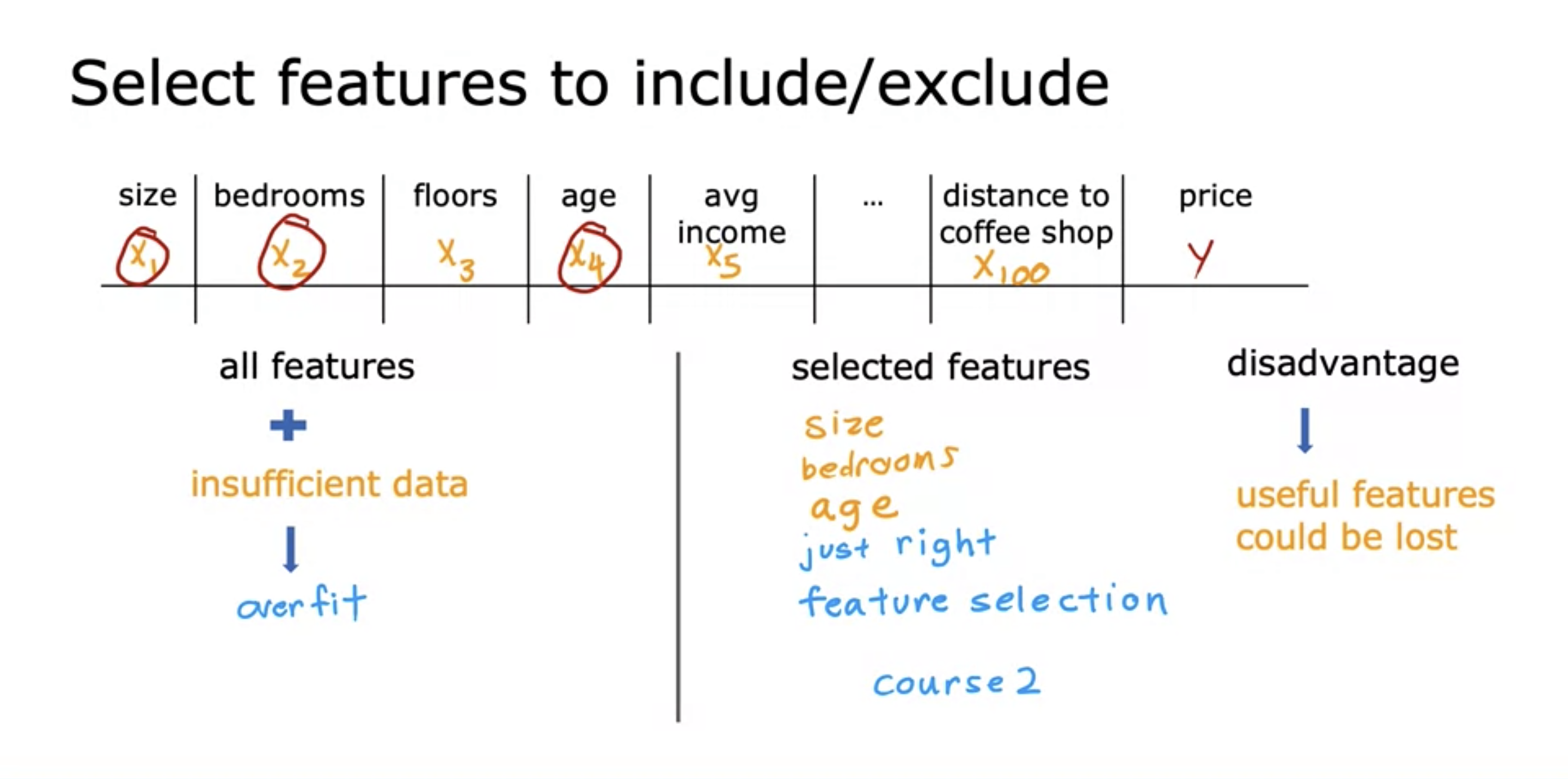
• Including every feature with insufficient data could lead to overfitting.
  • Maybe a graphical representation could help understanding this.
• Thus exclude unnecessary features.
• Disadvantage: useful features could be lost.
  • Course 2: algorithms for automatically choosing the most appropriate set of features to use for prediction task.

3. Regularization

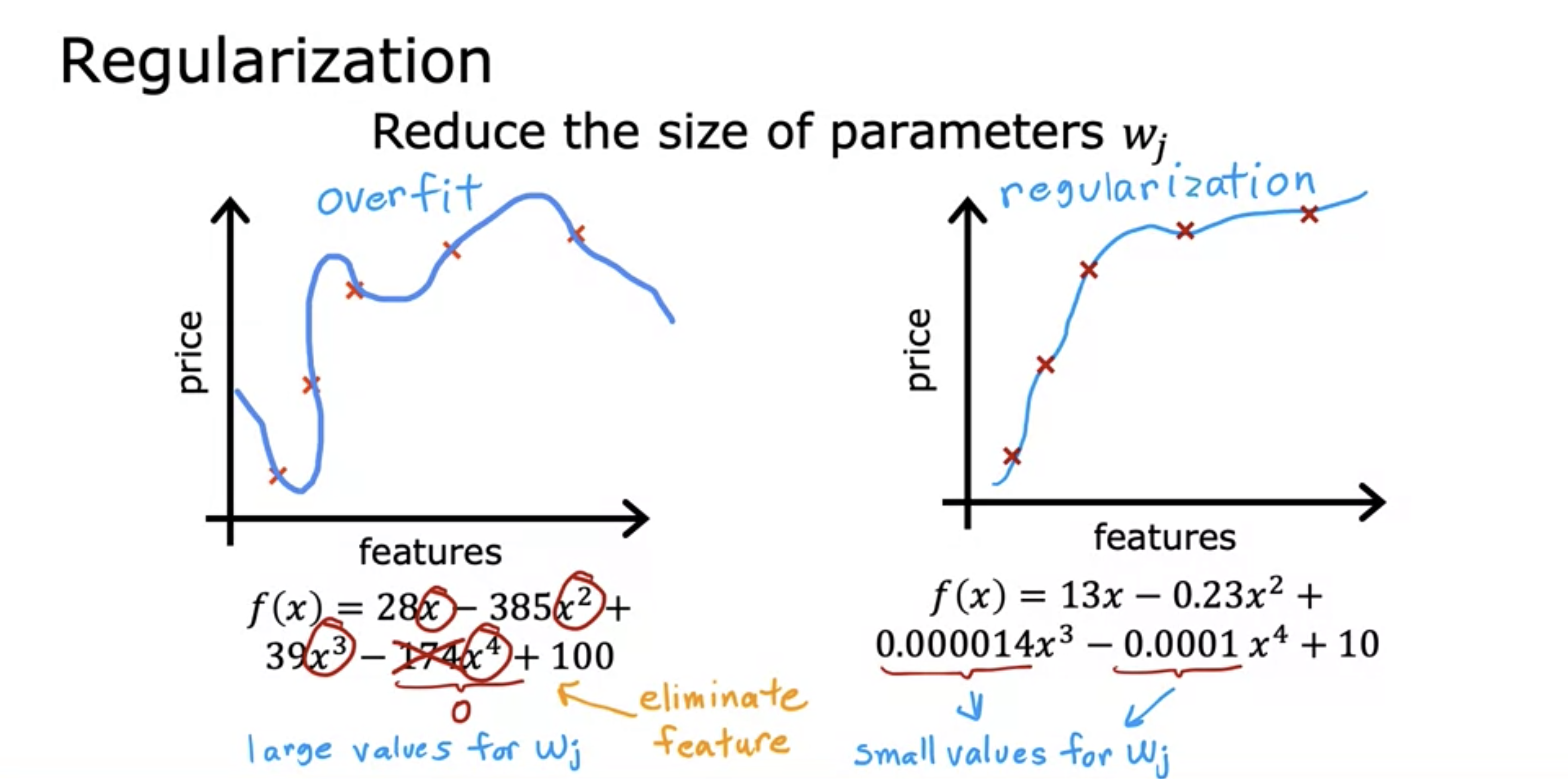
• Decrease the weight of a certain feature to minimize its impact on f(x).
• This can keep all the features and prevent any one of them from having a large effect, which may cause overfitting.

3. Cost Function with Regularization

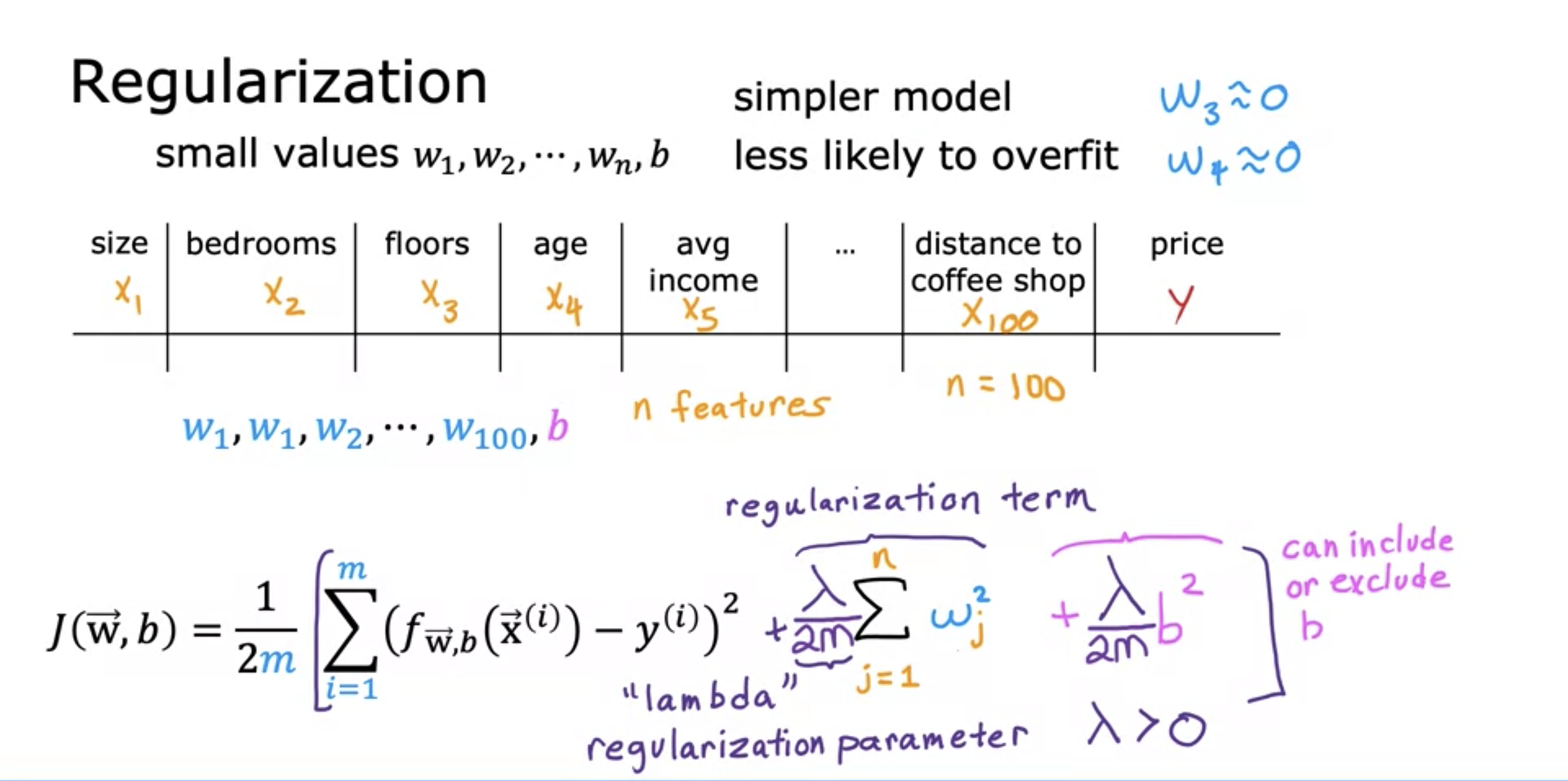
• Since we do not know which feature's weight must be decreased at first, we add regularization term to every feature's weight.

• Regularization term is added to the cost function, and the cost function is minimized.

• Small lambda value can cause overfit:

  • because weights are not decreased, large polynomial exponents can cause overfitting.

• Large value can cause underfit:

  • Large lambda means weights close to 0 - because when the cost function is minimized, in order to compensate for large regularization term, the weights will be close to 0 - , meaning that the model is close to a straight line.

• lambda is divided by 2m to keep the scale with the first term the same. This way with more training examples (higher m), the same lambda value can still be used.

• b^2 could also be added, but minimizing it has minimal effect.

4. Regularized Linear Regression

• 1 − α * λ/m term is close but less than 1, which decreases wj value after every iteration.

Cost Function Gradient Derivation

• The sigma is eliminated because when taking a partial derivative in terms of w_j, other w values are set to constant, which means they will become 0.
  • This leaves only w_j, which means there is no reason for a sigma.

Lab Examples:

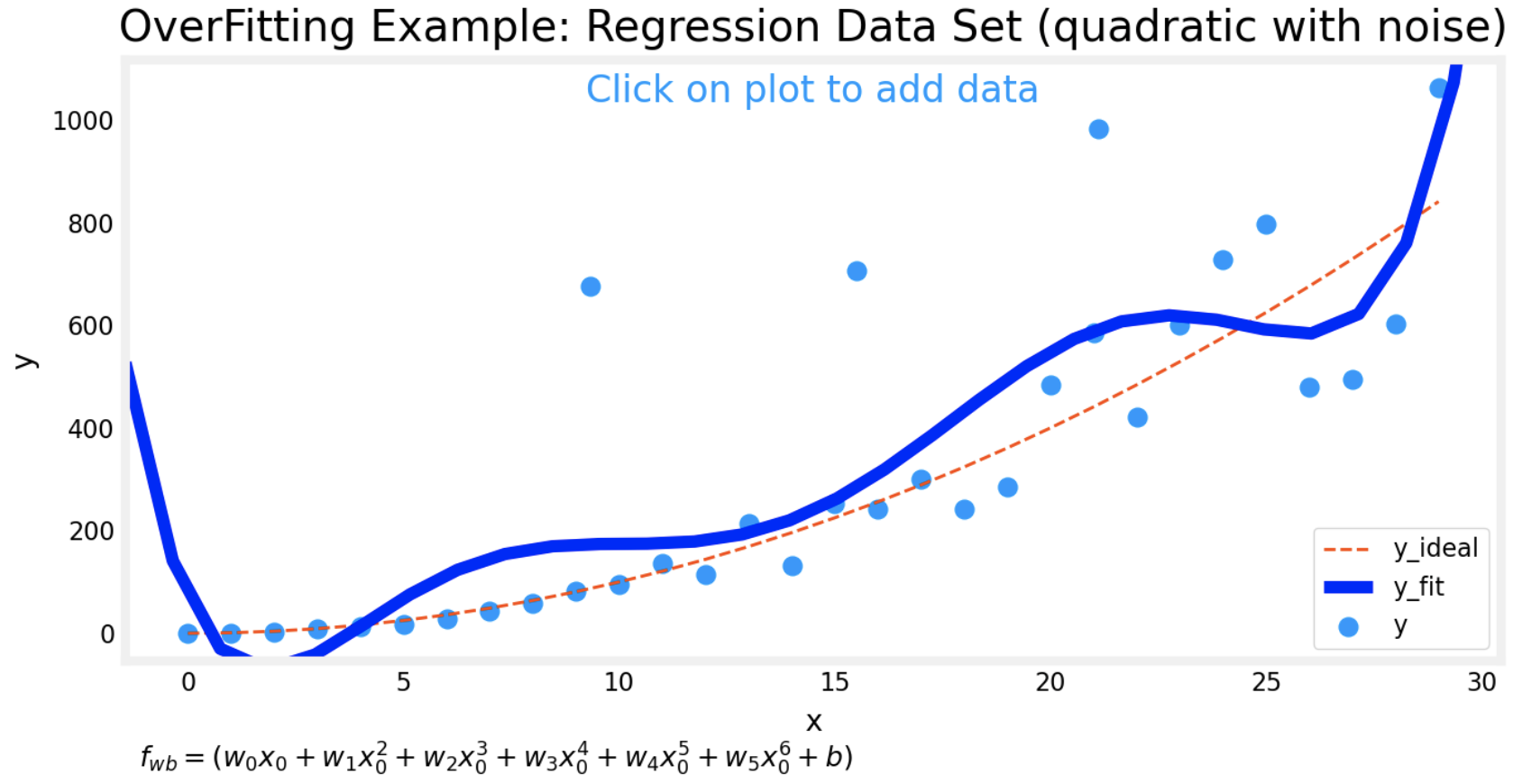
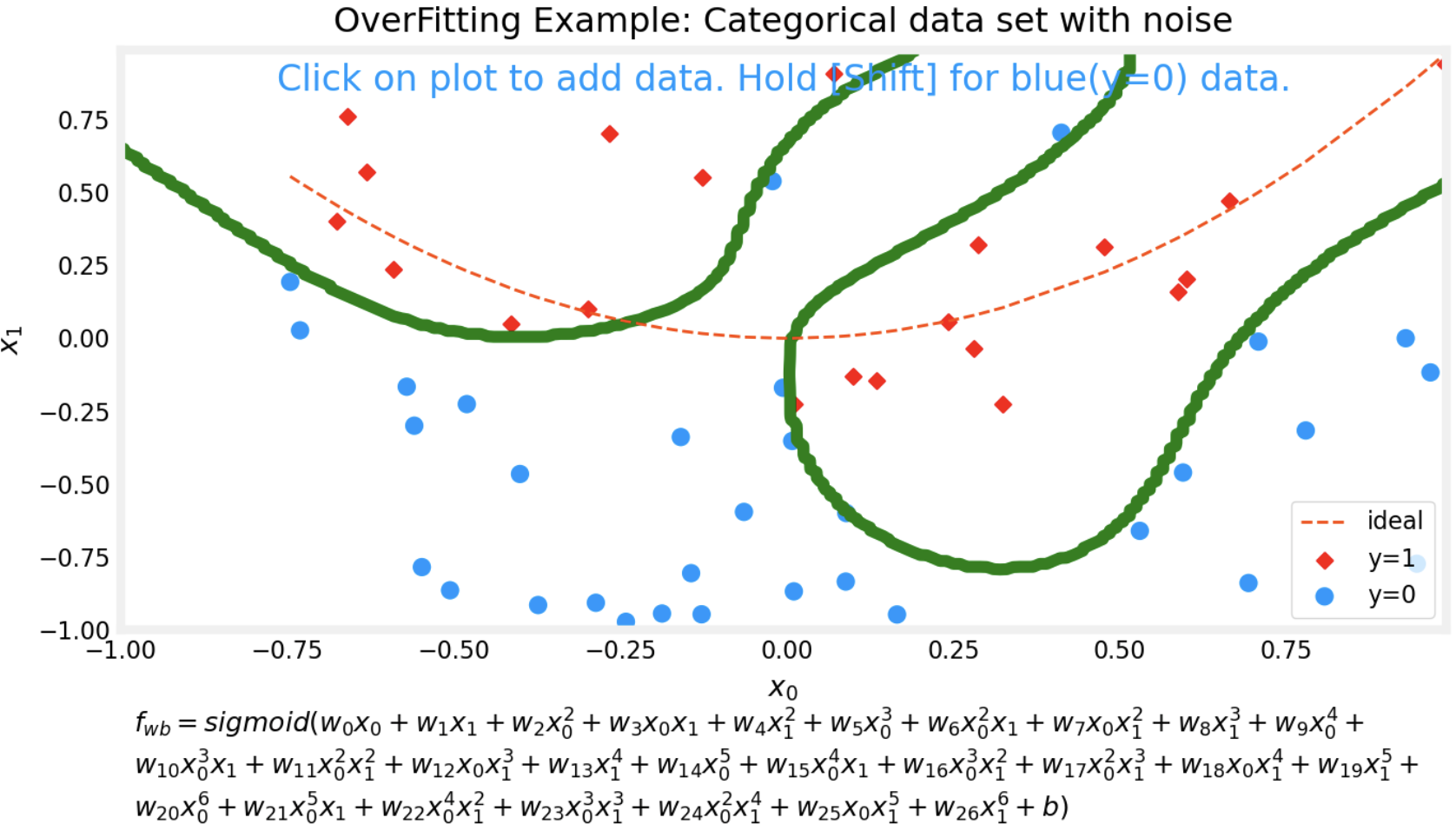
• This is a graph of regression data set with degree value of 6 and lambda value of 0.
• Because of outliers, the graph looks wiggly.
  
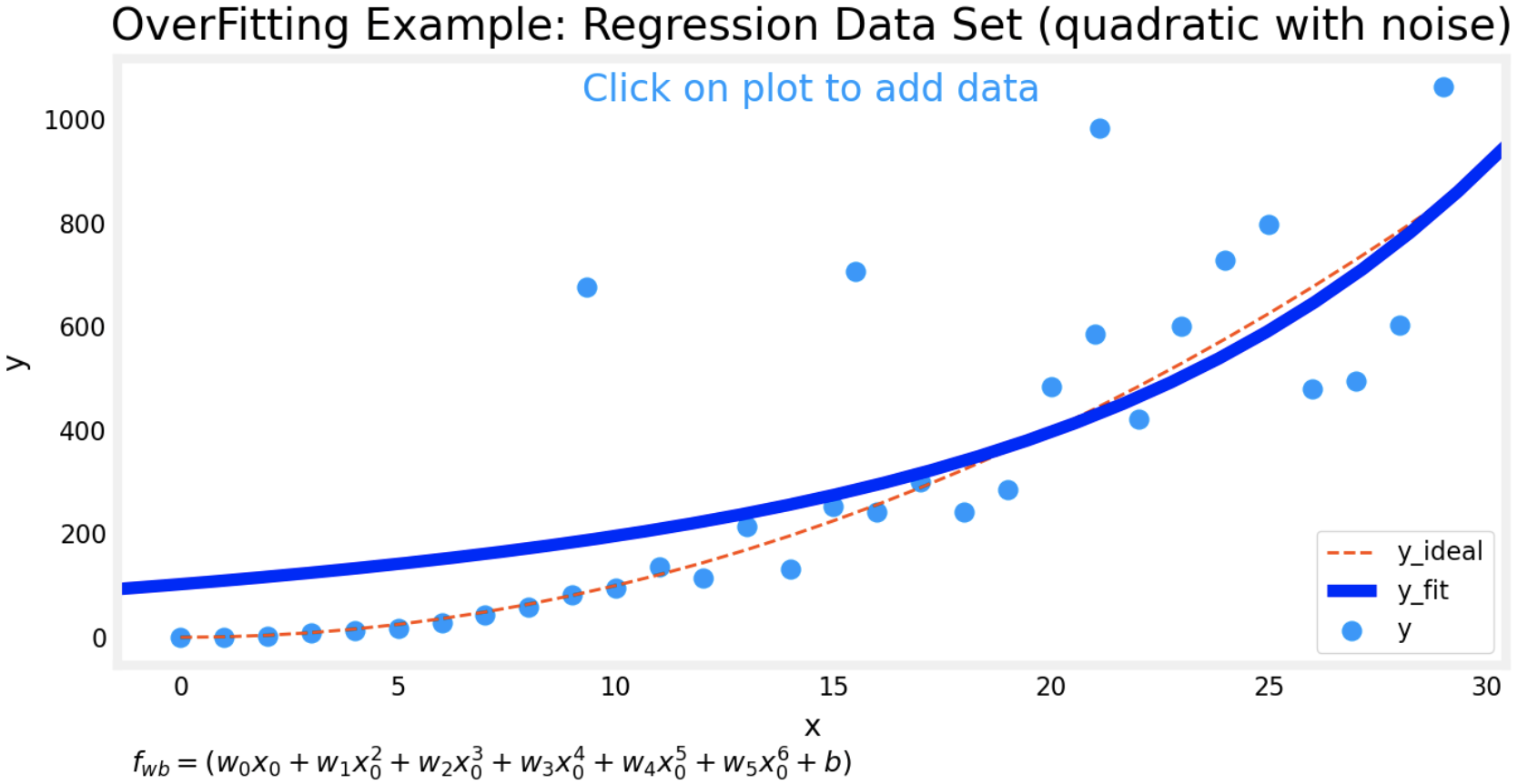
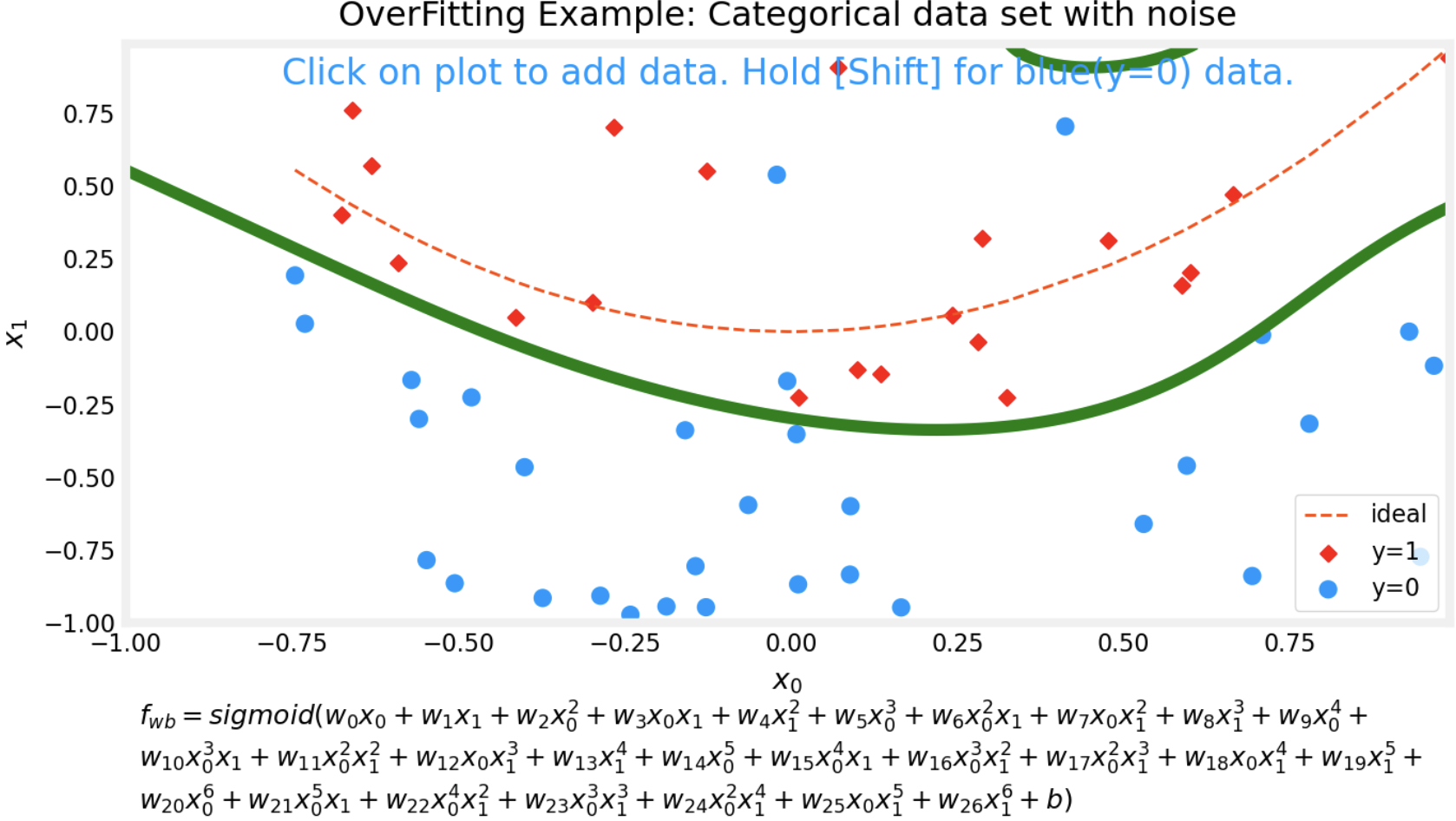
• With lambda value of 1, the graph looks more stable with less noise.
• The same happens with categorical data set.