[수학적 최적화] 2차원 선형 회귀 분석 (feat. numpy)

한결·2024년 1월 3일

수학 정리 노트

목록 보기

3/4

선형 회귀?

[서울시 CCTV 현황 분석]에서의 그래프의 모양을 확인해보겠습니다.

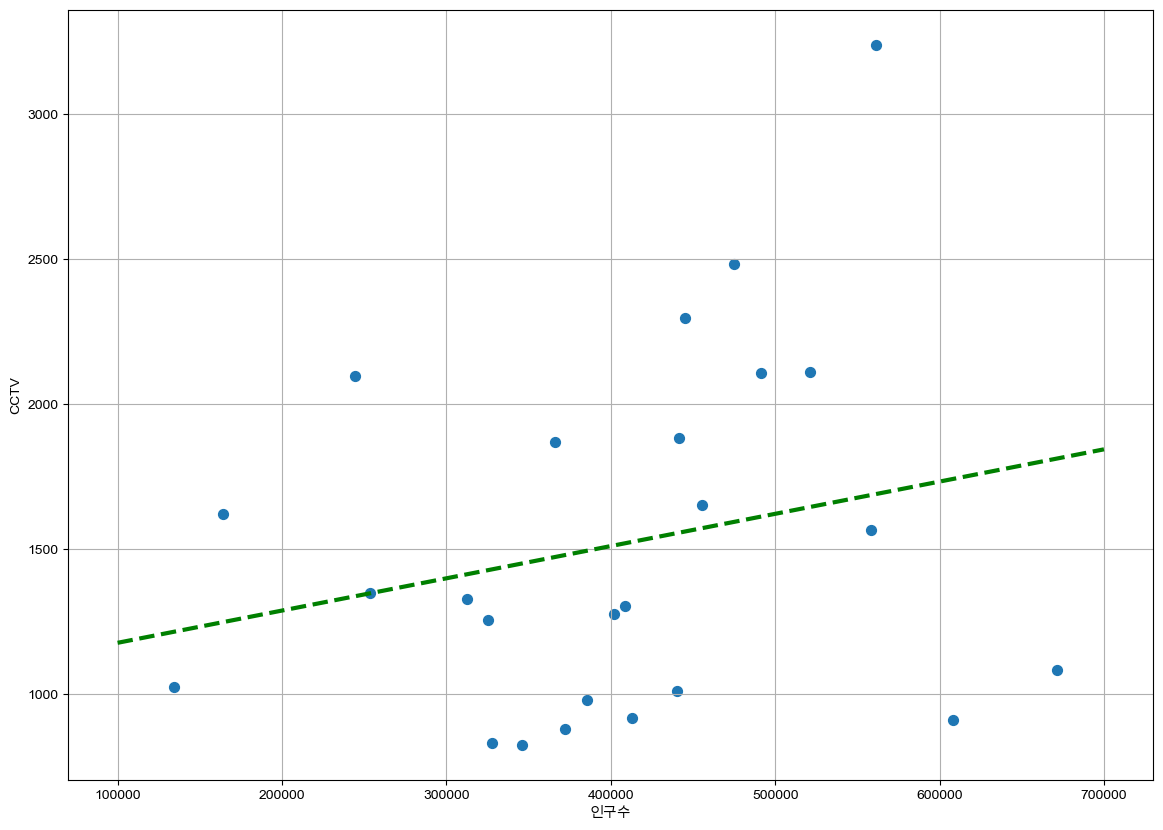
인구수가 증가하면서 설치된 CCTV의 개수도 점점 증가하는 것을 확인할 수 있었습니다. 이 때 저 초록색 선은 선형회귀를 통해 구한 추세선이에요. 즉 그래프 안에 있는 점들의 경향을 가장 수학적으로 잘 표현한 선이라 생각하면 됩니다. 이 직선을 구하는 방법을 우리는 선형 회귀 분석 이라고 합니다.

2차원 그래프에서 추세선은 일차함수입니다. 일차함수는 기울기와 절편만 알면 표현할 수 있다는 사실!

2차원 그래프에서 일차함수의 기울기와 절편을 구하는 방법은 대표적으로
np.polyfit(x, y, 1)
이 있습니다. 위 그래프 같은 경우 넘파이로 기울기와 y절편을 구해보겠습니다.

fp1 = np.polyfit(data_result['인구수'], data_result['소계'], 1)
fp1

array([1.11155868e-03, 1.06515745e+03])

그럼 오늘은 한번 이 기울기와 y절편이 어떻게 구해졌는지 한번 수학적인 과정과 코딩 구현까지 해볼게요!!

볼록 최적화

최적화?

수학적 최적화는 주어진 조건 하에서 최대값 혹은 최솟값을 찾는 과정입니다. 이걸 위해 보통 제약 조건이나 조건식이 있는데, 이를 만족하면서 가장 좋은 값을 찾는 게 최적화의 목표입니다.

표현방법은
$\text{minimize } f_0(x)$
$\text{subject to }$ 조건식

즉 '조건식에 맞춰서 $f_0(x)$ 의 최솟값을 구하라'고 해석하면 됩니다.

오늘은 다양한 최적화 방법 중 볼록성을 이용한 최적화를 이용해보겠습니다. 2차원 선형회귀 분석에 대한 얘기기 때문에 너무 딥하게 설명하지 않고 직관적으로 한번 짚고 넘어가 보겠습니다. 볼록성의 정의는 생략하겠습니다.

2차원에서

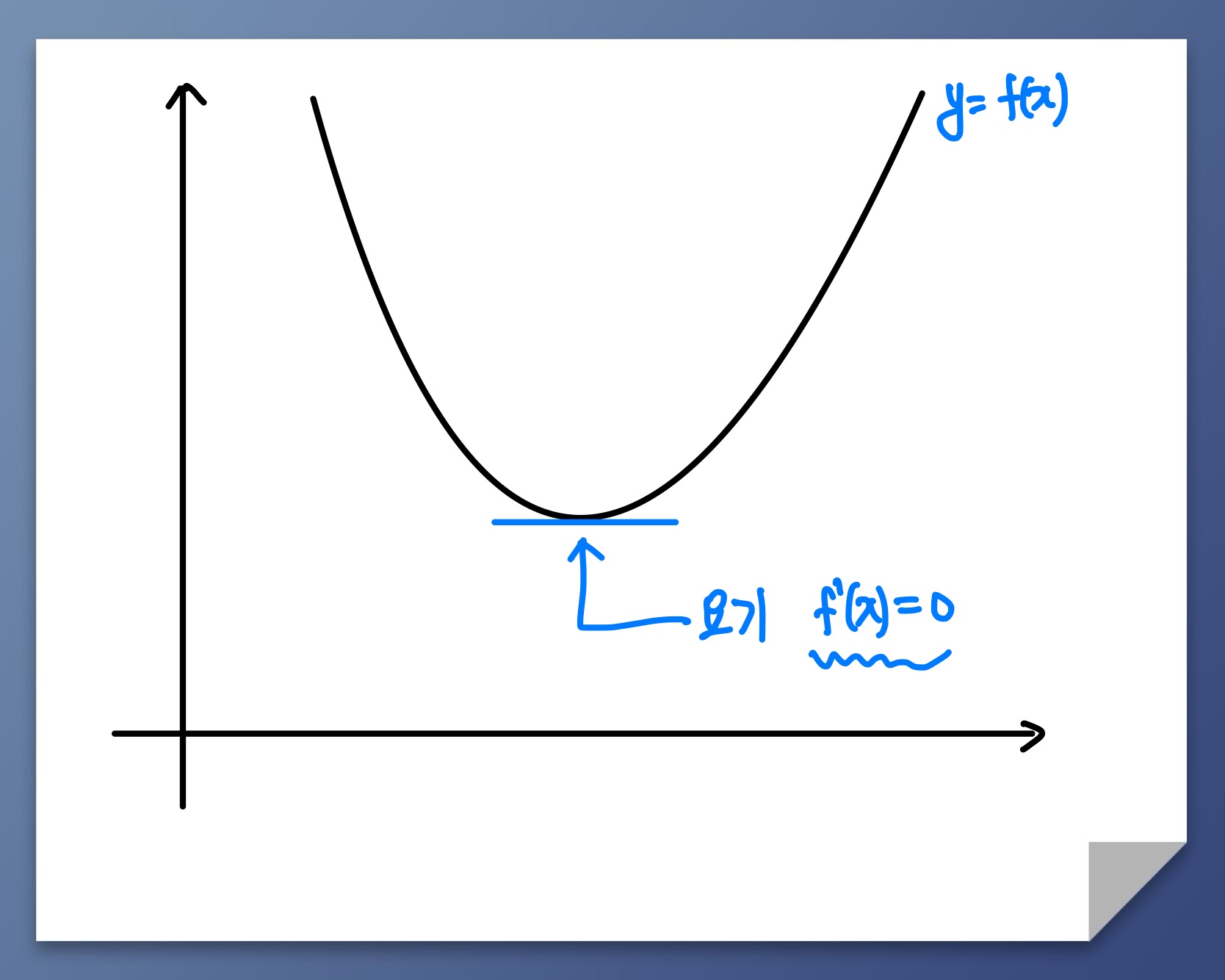
이차함수는 모든 실수에서 미분이 가능한 대표적인 볼록함수입니다. $y=f(x)$ 의 최솟값을 구하는 방법은 $f'(x)=0$ 인 점 즉 $f(x)$ 가 평평한 점을 구하면 됩니다.

3차원에서

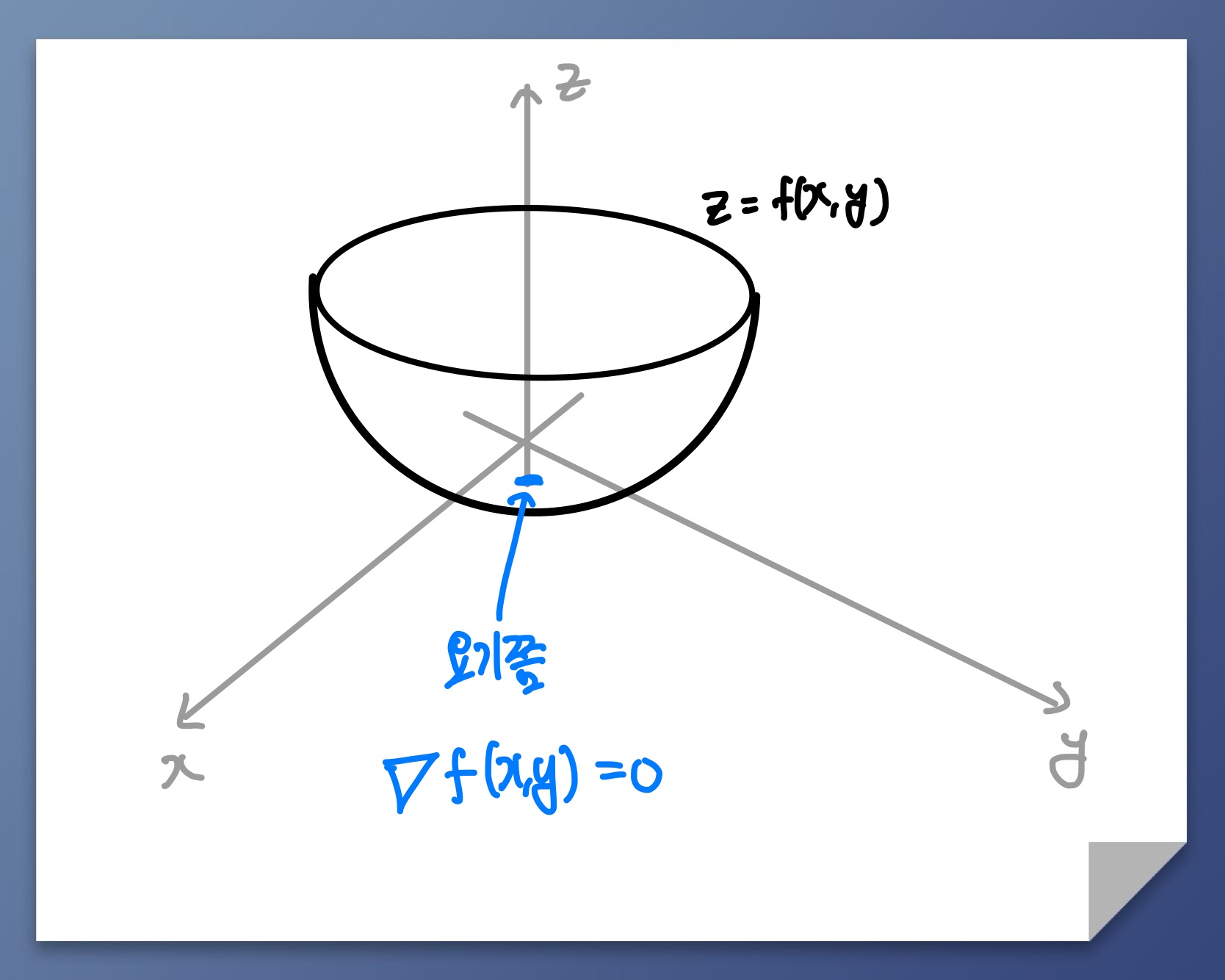
3차원도 마찬가지입니다. 만약 $f(x,y)$ 가 아래로 볼록인것을 확인했다면 $f(x,y)$ 가 최솟값이 나오는 지점은 $\nabla f(x,y)=0$ 즉 마찬가지로 평평한 지점입니다.

정리를 해보면

$f(x)$ 가 '아래로' 볼록인 함수이면 평평한 지점( $\nabla f(x)=0$ )에 해당하는 $x$ 가 최적화 문제의 해 즉 최솟값이 나오는 곳이다!

오차

오차란 예측한 값과 실제 값 사이의 차이를 말해요. 통계적으로 분석하거나 예측을 할 때, 모델이나 방법에 따라서 예측한 값과 실제 값 사이에 차이가 발생할 수 있습니다. 이 때 차이가 바로 오차입니다. 오차가 작을수록 예측이 정확하다고 볼 수 있습니다.

오차를 표현하는 식은 주로 쓰이는 세개를 나타내보면
1. MSE(Mean Squared Error)
$MSE = \frac{1}{N} \sum_{i=1}^{N}(pred_i - target_i)^2$

RMSE(Root Mean Squared Error)
$RMSE = \sqrt{\frac{1}{N} \sum_{i=1}^{N}(pred_i - target_i)^2}$

MAE(Mean Absolute Error)
$MAE = \frac{1}{N} \sum_{i=1}^{N}|(pred_i - target_i)|$

주어진 문제는? 🤔

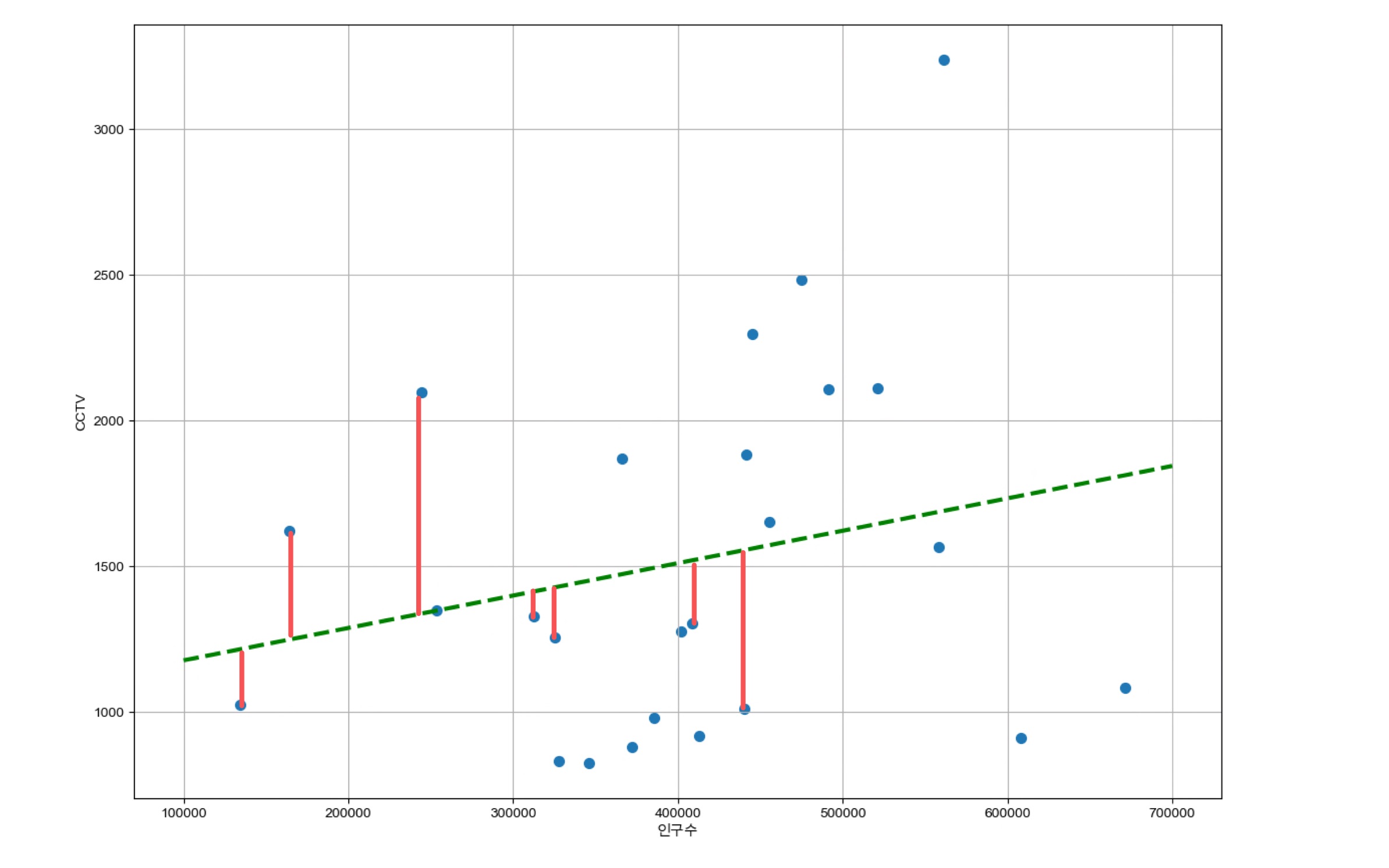
요런식으로 빨간선들이 각 점에서 직선까지의 차이라고 생각해볼게요. 이 차이들의 합이 결국 오차일 때 우리가 구하고자 하는 초록색선은 결국

'오차가 가장 작은 직선'

입니다.

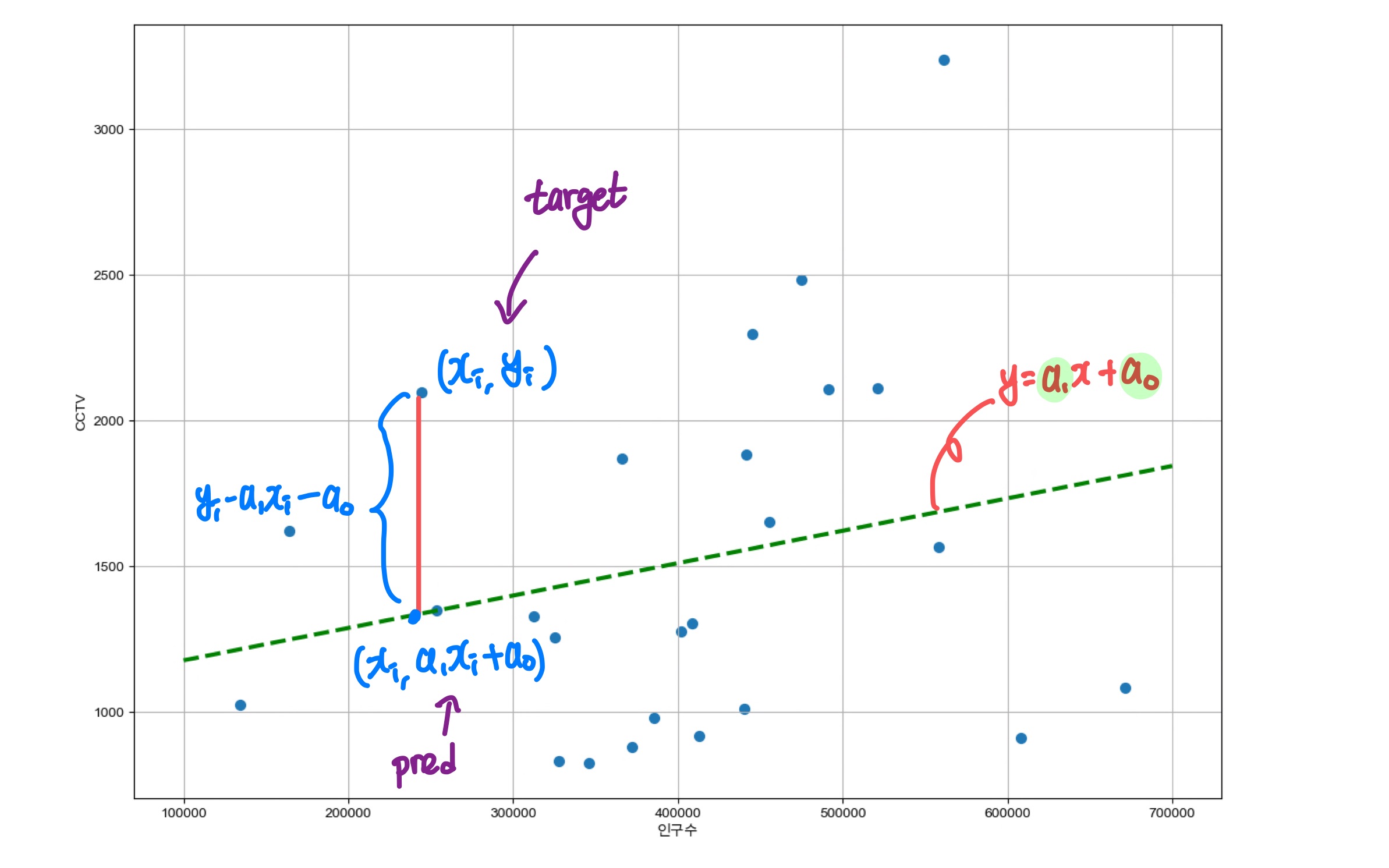
우리가 구하고자 하는 직선을 $y=a_1x+a_0$ 라고 뒀을 때 $(x_i, y_i)$ 에서 직선까지 빨간선의 길이는 $y_i - a_1x_i + a_0$ 로 표현할 수 있습니다.

이 때 오차식은 MSE를 사용하겠습니다.

아까 말했던 오차가 가장 작은 직선을 최적화 표현을 써보면

$minimize f(a_0,a_1) = \frac{1}{N} \sum_{i=1}^{N}(y_i - a_0 +a_1x_i)^2$

입니다. 즉 오차가 가장 최소가 나오는 $a_0, a_1$ 을 구하는 문제입니다.

해결 과정😇

❗ $f(a_0,a_1)=\frac{1}{N} \sum_{i=1}^{N}(y_i - a_0 +a_1x_i)^2$ 의 볼록성 증명은 이번글에서는 건너뛰겠습니다.🥲 볼록하다는 사실을 알고 문제를 해결해보겠습니다.

아까 볼록성을 이용해 최솟값을 구하는 방법인 $\nabla f(x)=0$ 을 이용하겠습니다.

Q. $\nabla f(a_0, a_1)=\Big(\frac{\partial f}{\partial a_0},\frac{\partial f}{\partial a_1}\Big) = (0, 0)$ 인 $a_0, a_1$ 을 구해보자.

정리하면
$a_1 = \frac{E(XY)-E(X)E(Y)}{V(X)}, a_0 = E(Y) - a_1 E(X)$ 이 나옵니다.

🧑🏻‍💻 2차 선형회귀분석 직접 코딩해보기

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
%matplotlib inline
from matplotlib import rc
rc('font', family='Arial Unicode MS')

# 랜덤 데이터 생성
np.random.seed(42)
x = np.linspace(1, 10, 10)  # 1부터 10까지의 10개의 값
y = 2 * x + 1 + np.random.randn(10)  # y = 2x + 1의 관계에 노이즈 추가

# 생성된 데이터 점 찍어보기
plt.scatter(x, y)
plt.xlabel('X 값')
plt.ylabel('Y 값')
plt.title('선형 회귀 분석을 위한 예시 데이터')
plt.show()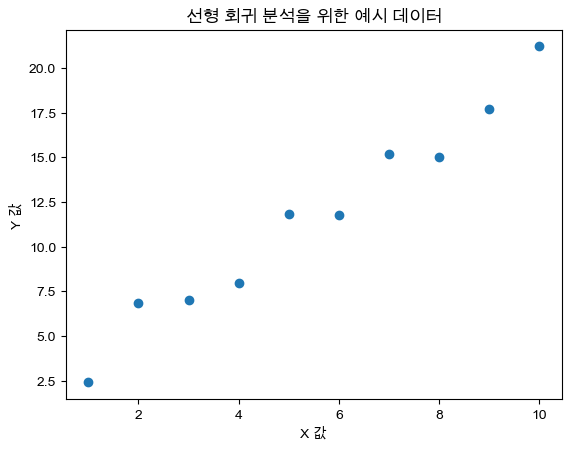

넘파이에서 기본으로 제공되는 함수로 계수를 계산해 보았습니다.

fp1 = np.polyfit(x, y, 1) # 직선을 구성하기 위한 계수 계산
f1 = np.poly1d(fp1)

fp1

array([1.86029898, 1.45824895])

이번엔 아까 구한 계수 공식을 활용해 직접 계산 해보겠습니다.

# 기댓값 함수
def expected_value(list_x):
    sum = 0
    for num in list_x:
        sum += num

    return sum / len(list_x)

# 분산 함수
def variance(list_x):
    return expected_value(x**2) - (expected_value(x)**2)

# 기울기 계수 함수
def a_1(list_x,list_y):
    return (expected_value(list_x * list_y) - expected_value(list_x) * expected_value(list_y))/variance(list_x)

# y 절편 계수 함수
def a_0(list_x,list_y):
    return expected_value(list_y) - (a_1(list_x,list_y) * expected_value(list_x))

# 결과 반환 함수
def my_polyfit(list_x, list_y):
    return np.array([a_1(list_x,list_y),a_0(list_x,list_y)])

my_polyfit(x,y)

array([1.86029898, 1.45824895])
토씨 하나 안 틀리고 넘파이랑 동일하게 나왔어요! 이럴 때 좀 뿌듯하네요😏

fx = np.linspace(0, 10) # x의 범위 지정
# 구해진 기울기와 절편을 이용해 일차함수 정의
line = my_polyfit(x,y)[0]*fx + my_polyfit(x,y)[1]

plt.plot(fx,line, ls='dashed', lw=3, color='grey')
plt.scatter(x,y)

plt.show()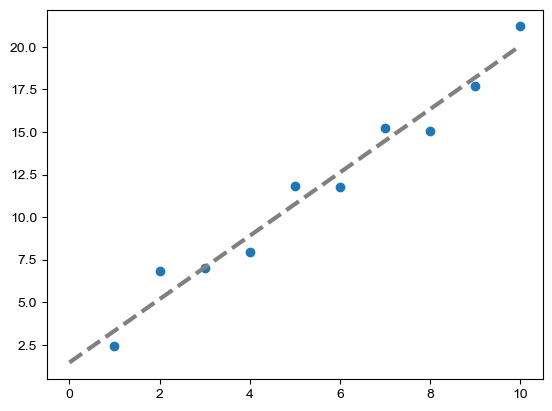

마치며...

2차원 선형 회귀 분석은 변수가 2개이기에 최적화 문제 중에 쉬운 편에 속합니다. 이 뒤에 다변량 데이터부터는 이렇게 깔끔하게 구할 수 있는 공식이 존재를 해도 해를 구하기가 매우 매우 까다로워지기 때문에 경사하강법 같은 방식을 사용해야 합니다.😇 당장 2차원 선형 회귀 분석을 완벽하게 정리하려면 볼록 최적화, 오차, 평균, 분산 등 알아야 하는 수학 지식이 많기에 이러한 것들도 차근차근 정리하며 공부해보겠습니다.