2차원 선형 회귀 분석을 읽고 오면 조금 더 이해가 편할 수 있습니다.

글 내용 순서는 '머신러닝을 위한 수학 - 이병준 저'를 참고했습니다.

경사하강법?

제가 만약 산 위에서 길을 잃었다고 가정하면 내려오는 방법은 그냥 계속 내리막을 타는 것입니다. 특히 경사가 가파른 길을 타고 내려올수록 밑에 도달하는 시간이 짧아질 겁니다. 이 글은 아래로 볼록인 함수의 최적화 문제를 해결하는 방법중 하나인 경사하강법의 수학적 원리에 대해 알아보겠습니다.

머신러닝, 딥러닝에서는 주로 언제 쓰이나요?🤔
기계학습에서 손실 함수(loss function)는 기계 학습 모델이 예측한 값과 실제 관측된 값 사이의 차이를 측정하는 함수입니다. 모델이 얼마나 정확한지를 평가하고, 이를 최소화하여 모델을 최적화하는 데 사용됩니다. 이 때 손실 함수의 최소값을 구할 때 경사하강법이 많이 쓰입니다.

---

경사하강법의 원리

하강법

(a) $x_{k+1} = x_{k} + t_k \Delta{x_k},k=0,1,...$ (단, $t_k>0$)
(b) $f(x_{k+1})<f(x_k)$

위의 조건을 가진 수식을 이용해 최적화 문제를 푸는 방식을 하강법이라 정의합니다. 즉 $k$가 증가하면 함수값이 계속 감소하도록 수열을 설정하는 것이 관건입니다.

---

경사하강법

경사하강법에 쓰이는 목적함수는 볼록함수입니다. 볼록함수의 정의에 의해

$f(x_{k+1}) \geq f(x_k)+\nabla f(x_k)^T(x_{k+1}-x_k)$

가 성립합니다. 이때 위 하강법 정의 (b)가 성립하려면

$\nabla f(x_k)^T(x_{k+1}-x_k)<0$이고 이식을 (a)를 이용해 정리하면

$\nabla f(x_k)^T t_k\Delta{x_k}<0$ 이 되어야 합니다.

$t_k$는 양수이기에 $\Delta{x_k}$를 설정하겠습니다.

❗️ 다변수 함수 $f:R^n \rightarrow R$이 가장 빠르게 증가하는 방향은 $\nabla f$ 방향이다.

위 정리를 거꾸로 말하면 $\Delta{x_k}$를 $-\nabla f(x_k)$로 놓으면 가장 빠르게 감소하는 방향으로 $x_k$가 향한다는 것을 알 수 있습니다.

그럼 이것을 파이썬으로 구현해보고 그래프로 한번 확인해보겠습니다.

🧑🏻‍💻 경사하강법 코딩하기

$f(x) = 2x^2+3xy+4y^2$ 일 때, $minimize_{x \in R^2} f(x)$를 경사하강법을 이용해 풀어보세요. (단, $x_0=(2,4), t_k=0.01, \epsilon=10^{-8}$)

# 목적함수
def f(x,y):
    return 2*x**2 + 3*x*y + 4*y**2

# 목적함수를 x로 편미분한 함수
def fx(x,y):
    return 4*x+3*y

# 목적함수를 y로 편미분한 함수
def fy(x,y):
    return 3*x+8*y

# x_k,y_k의 좌표를 받을 리스트
xlist,ylist=[2],[4]

# 설정 값
x0,y0 = 2,4
t=0.01
eps=10**(-8)

iter=0
xk,yk=x0,y0

while True:
    tk=t
    
    # xkp1 = xk - tk * delta(xk)
    xkp1=xk-tk*fx(xk,yk)
    ykp1=yk-tk*fy(xk,yk)

    xlist.append(xkp1)
    ylist.append(ykp1)

    if np.linalg.norm(np.array((xkp1-xk,ykp1-yk)))<eps:
        print(f'iterated {iter} times')
        print(f'GD converges to {round(xkp1,1),round(ykp1,1)}')
        break

    iter = iter + 1
    xk,yk = xkp1, ykp1

520번 경사하강법을 실행해서 (0,0) 즉 해에 수렴하는 것을 확인할 수 있습니다.

---

🧑🏻‍💻 경사하강법 그래프

from mpl_toolkits.mplot3d import axes3d
import matplotlib.pyplot as plt
from matplotlib import animation

# x,y 값에 따른 z 좌표 리스트
zlist=[]
for i in range(len(xlist)):
	zlist.append(f(xlist[i],ylist[i]))
    
# 그래프 생성
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.view_init(elev=30, azim=-30) 

# x, y 값 생성
x = np.linspace(-4, 4, 10)
y = np.linspace(-4, 4, 10)
x, y = np.meshgrid(x, y)

# z 값 계산
z = f(x,y)

# 3D 플로팅
ax.plot_surface(x,y,z,color='#d070fb', alpha = 0.6)
ax.plot(xlist,ylist,zlist,lw=3, color='black')
ax.text(xlist[0],ylist[0],zlist[0],'(x0,y0,f(x0,y0))')
ax.text(xlist[-1],ylist[-1],zlist[-1],'Solution')

# x, y, z 축 레이블 설정
ax.set_xlabel('X-axis')
ax.set_ylabel('Y-axis')
ax.set_zlabel('Z-axis')

# 그래프 표시
plt.show()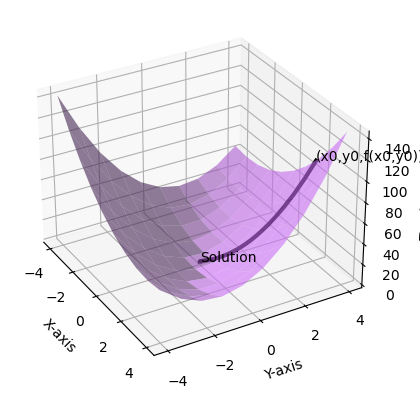

경사를 따라 쭉 내려가 (0,0)에 수렴하는 것을 확인할 수 있습니다.

---