[선형대수학]특잇값 분해

• 정방행렬 => 고유분해를 통해 고윳값, 고유벡터를 찾음
• 정방행렬이 아닌 행렬 => 특이분해를 통해 특잇값, 특이벡터를 찾음

1. 특잇값과 특이벡터

특잇값 분해(Singular value decomposition)
= 특이분해(Singular decomposition)
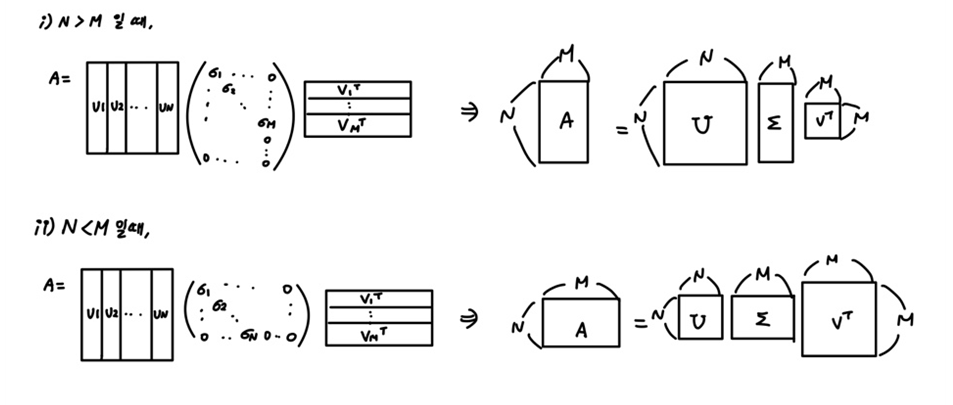
: NxM 크기의 행렬A를 다음과 같이 3개의 행렬 곱으로 나타낸 것

• 특이분해는 모든 행렬에 대해 가능하다

2. 특잇값 분해 행렬의 크기

특잇값 개수는 행렬의 열과 행 중 작은 값과 같다.

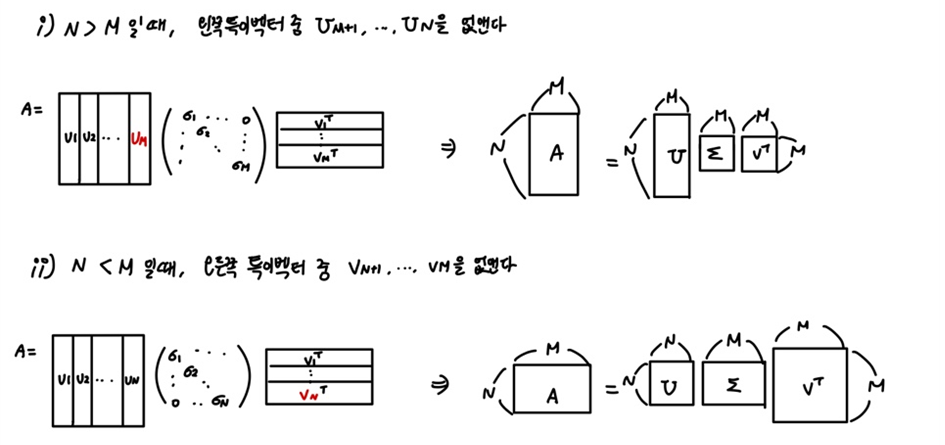
3. 특잇값 분해의 축소형

특잇값 대각행렬에서 0인 부분은 사실상 의미가 없기 때문에, 대각행렬의 0 원소 부분과 이에 대응하는 왼쪽(또는 오른쪽) 특이벡터들을 없애고 축소된 형태로 해도 마찬가지로 원래 행렬이 나온다.

+) 특잇값 분해, 축소형을 python으로 구현

import numpy as np
from numpy.linalg import svd

#특잇값 분해는 svd함수 사용
A = np.array([[3, -1], [1, 3], [1, 1]])
U, S, VT = svd(A)

#U출력
U

#<output>
# array([[-4.08248290e-01,  8.94427191e-01, -1.82574186e-01],
       [-8.16496581e-01, -4.47213595e-01, -3.65148372e-01],
       [-4.08248290e-01, -2.06937879e-16,  9.12870929e-01]])

#S출력
S

#<output>
# array([3.46410162, 3.16227766])

#S의 특잇값을 대각성분으로 하는 대각행렬 생성
# 단, 행렬 A가 2X3이었다면 np.diag(np.append(S,0))[:2,:]
  
np.diag(S, 1)[:, 1:]
  
#<output>
#  array([[3.46410162, 0.        ],
#     [0.        , 3.16227766],
#     [0.        , 0.        ]])

#VT출력
VT

#<output>
#  array([[-0.70710678, -0.70710678],
#    [ 0.70710678, -0.70710678]])

# 아래의 결과가 행렬 A와 같음
U @ np.diag(S, 1)[:, 1:] @ VT

# <output>
# array([[ 3., -1.],
#     [ 1.,  3.],
#     [ 1.,  1.]])

축소형의 경우 인수 full_matrices=False로 지정

U2, S2, VT2 = svd(A, full_matrices=False)
U2 @ np.diag(S2) @ VT2

#<output>
#array([[ 3., -1.],
#       [ 1.,  3.],
#       [ 1.,  1.]])

4. 특잇값과 특이벡터의 관계

i 번째 특잇값 σi와 특이벡터 ui, vi는
Avi=σiui(i=1,…,min(M,N))

(증명)

5. 특이분해와 고유분해의 관계

• 행렬 A의 특잇값제곱 = 분산행렬 A^TA 의 고윳값
• 행렬 A의 오른쪽 특이벡터 = 분산행렬 A^TA 의 고유벡터

데이터 사이언스 스쿨

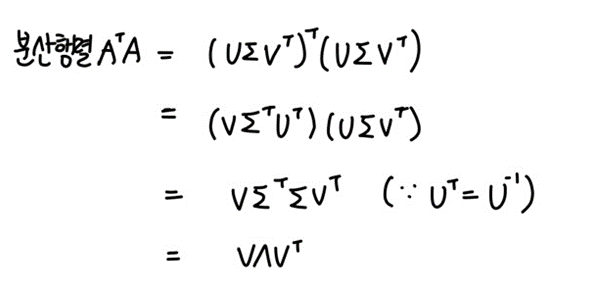
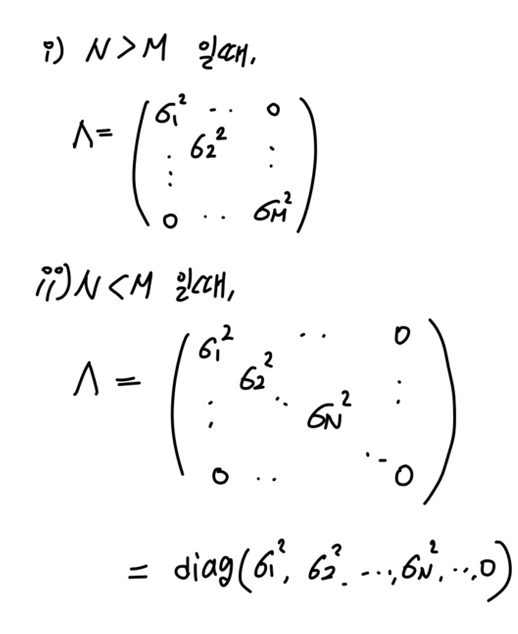
위의 링크를 참고하여 학습했습니다:)