[LeetCode] 1161. Maximum Level Sum of a Binary Tree

1. Question

Given the root of a binary tree, the level of its root is 1, the level of its children is 2, and so on.

Return the smallest level x such that the sum of all the values of nodes at level x is maximal.

Example 1:

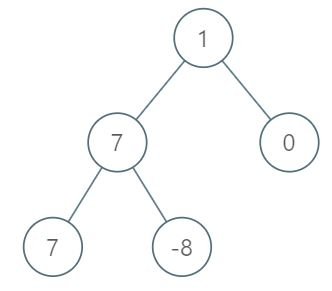
Input: root = [1,7,0,7,-8,null,null]
Output: 2
Explanation: 
Level 1 sum = 1.
Level 2 sum = 7 + 0 = 7.
Level 3 sum = 7 + -8 = -1.
So we return the level with the maximum sum which is level 2.

Example 2:

Input: root = [989,null,10250,98693,-89388,null,null,null,-32127]
Output: 2

2. Thoughts

Use BFS.
1. Iterate through every level of the tree.
2. calculate sum for level
3. return level for max sum

3. Tips learned

4. My solution

class Solution:
    def maxLevelSum(self, root: Optional[TreeNode]) -> int:
        final_max = root.val
        current_level, max_level = 0, 1
        tree = deque([root])

        while tree:
            current_level += 1
            level = len(tree)
            local_sum = 0
            for _ in range(level):
                node = tree.popleft()
                local_sum += node.val
                if node.left:
                    tree.append(node.left)
                if node.right:
                    tree.append(node.right)
            if local_sum > final_max:
                final_max = local_sum
                max_level = current_level

        return max_level

41/41 cases passed (226 ms)
Your runtime beats 80.42 % of python3 submissions
Your memory usage beats 21.99 % of python3 submissions (21.1 MB)

5. AI Solution and Improvements

Your solution for finding the level of a binary tree with the maximum sum is effective and follows a standard approach using Breadth-First Search (BFS) with a queue. The logic is sound, and the code is well-structured. However, there is a minor optimization that can be done to enhance readability and efficiency.

In your current implementation, you initialize current_level to 0 and increment it at the start of the while loop. This works perfectly, but it can be slightly more intuitive if you start counting levels from 1 (since the root is at level 1) and increment it at the end of the loop. Also, initializing final_max with root.val is fine, but in case of a tree with all negative values, it might cause an issue if the root has a very low value. A better approach could be to initialize it with the smallest possible integer.

Here's an optimized version of your code:

from collections import deque

class Solution:
    def maxLevelSum(self, root: Optional[TreeNode]) -> int:
        if not root:
            return 0

        final_max = float('-inf')  # Initialize to the smallest possible integer
        max_level = 1
        current_level = 1
        queue = deque([root])

        while queue:
            level_size = len(queue)
            local_sum = 0
            for _ in range(level_size):
                node = queue.popleft()
                local_sum += node.val
                if node.left:
                    queue.append(node.left)
                if node.right:
                    queue.append(node.right)

            if local_sum > final_max:
                final_max = local_sum
                max_level = current_level

            current_level += 1  # Increment the level after processing the current level

        return max_level

In this revised version, current_level starts at 1, and final_max is initialized to float('-inf') to handle all negative value cases more effectively. Incrementing current_level after processing each level makes the code more intuitive.