[LeetCode] 450.Delete Node in a BST

1. Question

Given a root node reference of a BST and a key, delete the node with the given key in the BST. Return the root node reference (possibly updated) of the BST.

Basically, the deletion can be divided into two stages:

Search for a node to remove.
If the node is found, delete the node.

Example 1:

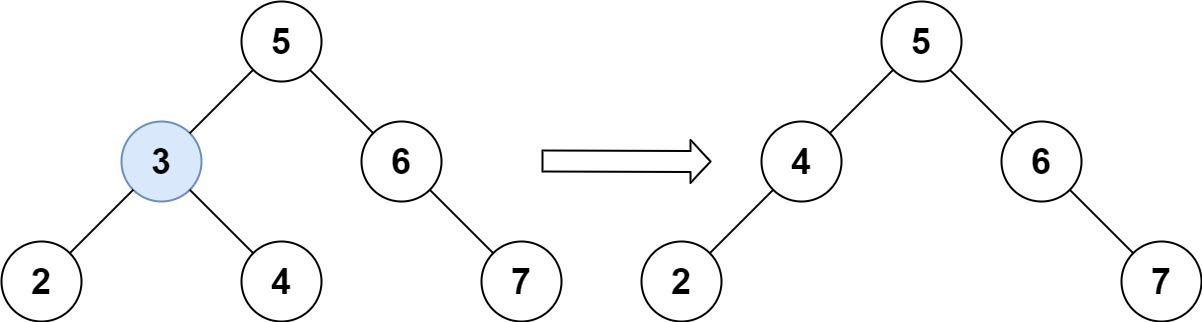
Input: root = [5,3,6,2,4,null,7], key = 3
Output: [5,4,6,2,null,null,7]
Explanation: Given key to delete is 3. So we find the node with value 3 and delete it.
One valid answer is [5,4,6,2,null,null,7], shown in the above BST.
Please notice that another valid answer is [5,2,6,null,4,null,7] and it's also accepted.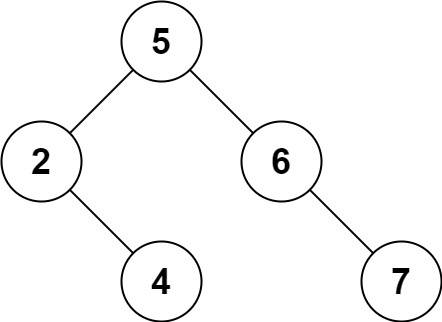

Example 2:

Input: root = [5,3,6,2,4,null,7], key = 0
Output: [5,3,6,2,4,null,7]
Explanation: The tree does not contain a node with value = 0.

Example 3:

Input: root = [], key = 0
Output: []

2. Thoughts

Use Binary Tree characteristic
change to leftmost of right
if no right exists, change to left

3. Tips learned

4. My solution

class Solution:
    def deleteNode(self, root: Optional[TreeNode], key: int) -> Optional[TreeNode]:
        def changeto_leftmost_right(node, dir):
            if dir == "right":
                child = node.right
            elif dir == "left":
                child = node.left
            else:
                child = node

            temp = child.right
            if not temp.left:
                if dir == "right":
                    node.right = temp
                elif dir == "left":
                    node.left = temp

                temp.left = child.left
                return

            while temp.left.left:
                temp = temp.left

            child.val = temp.left.val
            temp.left = temp.left.right

        def changeto_left(node, dir):
            if dir == "right":
                node.right = node.right.left
            else:
                node.left = node.left.left

        if not root:
            return None

        if key == root.val:
            if not root.right and not root.left:
                return None
            elif root.right:
                if not root.right.left:
                    changeto_leftmost_right(root, "root")
                    return root.right
                else:
                    changeto_leftmost_right(root, "root")
            elif root.left:
                return root.left

        node = root
        while node.right or node.left:
            if key > node.val:
                if not node.right:
                    return root
                if key == node.right.val:
                    if node.right.right:
                        changeto_leftmost_right(node, "right")
                    elif node.right.left:
                        changeto_left(node, "right")
                    else:
                        node.right = None
                else:
                    node = node.right
            else:
                if not node.left:
                    return root
                if key == node.left.val:
                    if node.left.right:
                        changeto_leftmost_right(node, "left")
                    elif node.left.left:
                        changeto_left(node, "left")
                    else:
                        node.left = None
                else:
                    node = node.left

        return root

92/92 cases passed (62 ms)
Your runtime beats 91.5 % of python3 submissions
Your memory usage beats 21.61 % of python3 submissions (20.8 MB)

5. AI Solution and Improvements

Your implementation for deleting a node in a binary search tree (BST) seems comprehensive, but it can be simplified for better readability and efficiency. The main idea when deleting a node from a BST is to maintain the BST properties after the deletion. Here are the key steps to consider:

1. Find the node to delete: Traverse the tree to find the node with the given key.
2. Handle different cases for deletion:
   • If the node is a leaf (no children), simply remove it.
   • If the node has one child, replace it with its child.
   • If the node has two children, find the in-order successor (smallest node in the right subtree) or the in-order predecessor (largest node in the left subtree), copy its value to the node, and delete the in-order successor/predecessor.

Here's a simplified version of your code implementing these steps:

class Solution:
    def deleteNode(self, root: TreeNode, key: int) -> TreeNode:
        if not root:
            return root

        # Find the node to be deleted
        if key < root.val:
            root.left = self.deleteNode(root.left, key)
        elif key > root.val:
            root.right = self.deleteNode(root.right, key)
        else:
            # Node with only one child or no child
            if not root.left:
                return root.right
            elif not root.right:
                return root.left

            # Node with two children: Get the inorder successor (smallest in the right subtree)
            temp = self.findMin(root.right)

            # Copy the inorder successor's content to this node
            root.val = temp.val

            # Delete the inorder successor
            root.right = self.deleteNode(root.right, temp.val)

        return root

    def findMin(self, node):
        current = node
        while current.left is not None:
            current = current.left
        return current

This code simplifies the deletion process and improves readability. The recursive approach makes it easier to handle the different cases of node deletion in a BST.