[LeetCode] 872. Leaf-Similar Trees

1. Question

Consider all the leaves of a binary tree, from left to right order, the values of those leaves form a leaf value sequence.

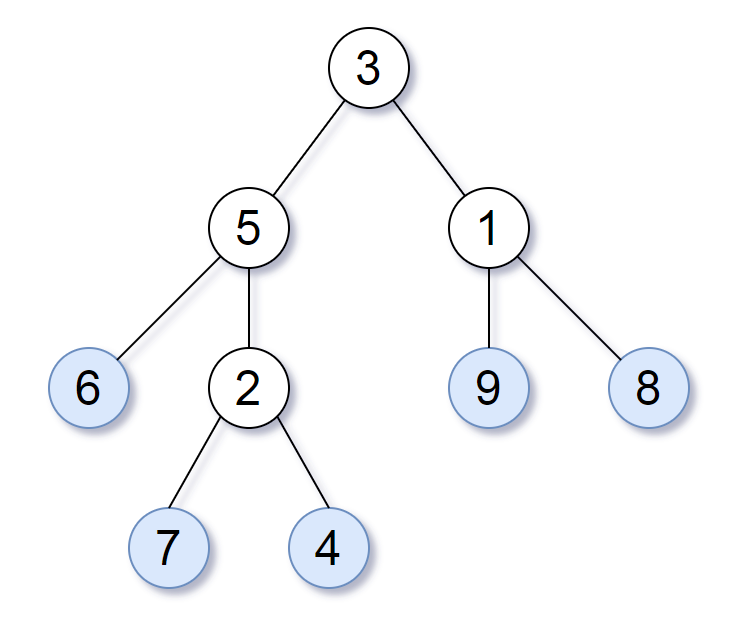
For example, in the given tree above, the leaf value sequence is (6, 7, 4, 9, 8).

Two binary trees are considered leaf-similar if their leaf value sequence is the same.

Return true if and only if the two given trees with head nodes root1 and root2 are leaf-similar.

Example 1:

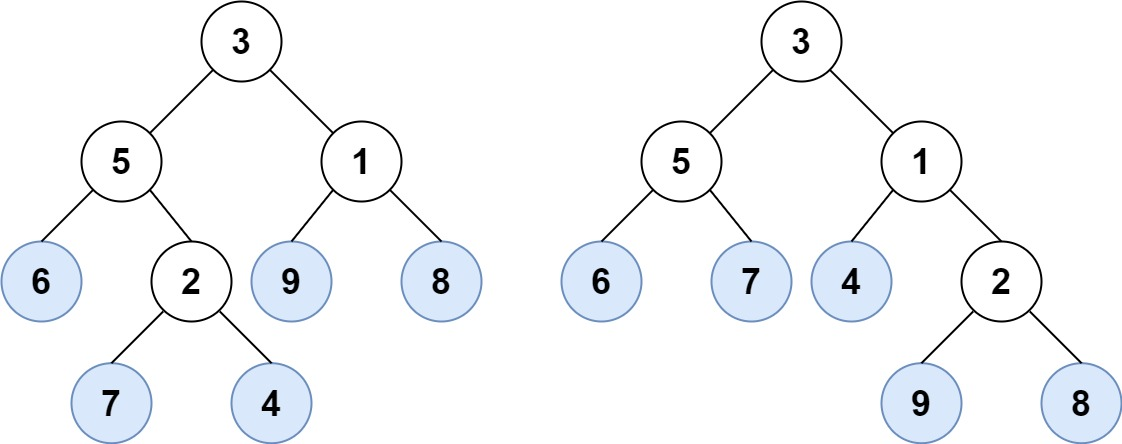
Input: root1 = [3,5,1,6,2,9,8,null,null,7,4], root2 = [3,5,1,6,7,4,2,null,null,null,null,null,null,9,8]
Output: true

Example 2:

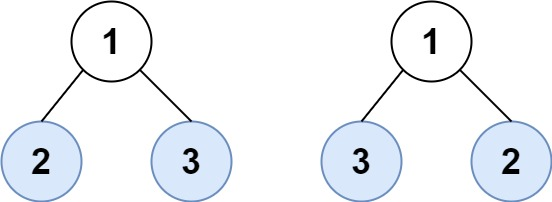
Input: root1 = [1,2,3], root2 = [1,3,2]
Output: false

2. Thoughts

Use DFS

3. Tips learned

4. My solution

class Solution:
    def leafSimilar(self, root1: Optional[TreeNode], root2: Optional[TreeNode]) -> bool:
        tree1, tree2 = deque([root1]), deque([root2])
        leaf = []

        while tree1:
            n = tree1.pop()

            if not n.right and not n.left:
                leaf.append(n.val)
            else:
                if n.right:
                    tree1.append(n.right)
                if n.left:
                    tree1.append(n.left)
        while tree2:
            n = tree2.pop()
            if not n.right and not n.left:
                if not leaf or leaf[-1] != n.val:
                    return False
                else:
                    leaf.pop()
            else:
                if n.left:
                    tree2.append(n.left)
                if n.right:
                    tree2.append(n.right)

        return not leaf

43/43 cases passed (35 ms)
Your runtime beats 85.91 % of python3 submissions
Your memory usage beats 31.76 % of python3 submissions (16.3 MB)

5. AI Solution and Improvements

Your solution to determine if two binary trees are leaf-similar is conceptually sound but can be improved for clarity and efficiency. The current implementation uses a deque and a list to store leaf nodes, but this can be simplified by using a depth-first search (DFS) approach to directly compare the leaf nodes of both trees as they are encountered. Here's how you can improve it:

Improved Solution

1. Use Recursive DFS to Collect Leaf Values: Create a helper function that performs a DFS and collects the leaf values in a list. This function can be applied to both trees to get their leaf sequences.

2. Compare Leaf Sequences: Compare the leaf sequences of the two trees to determine if they are leaf-similar.

Here's the revised code:

class Solution:
    def leafSimilar(self, root1: Optional[TreeNode], root2: Optional[TreeNode]) -> bool:
        def dfs(node):
            if not node:
                return []
            if not node.left and not node.right:
                return [node.val]
            return dfs(node.left) + dfs(node.right)

        return dfs(root1) == dfs(root2)

Explanation

• DFS to Find Leaf Nodes: The dfs function is a recursive function that traverses the tree. If it encounters a leaf node (a node without children), it returns its value. Otherwise, it recursively collects leaf values from both the left and right subtrees.

• Comparing Leaf Sequences: After obtaining the leaf sequences from both trees using DFS, the sequences are compared using ==. If they are the same, the function returns true, indicating the trees are leaf-similar.

Benefits of the Improved Solution

• Simplicity and Readability: The code is more straightforward, focusing on the task of finding leaf sequences and comparing them.
• Efficiency: This approach is more efficient as it avoids extra data structures like deques and simplifies the logic, especially in the way leaf nodes are compared.
• Scalability: The DFS approach is more scalable and works efficiently even for large trees.