[LeetCode / C++] 1091. Shortest Path in Binary Matrix

Leetcode Question Link

1. Question

Given an n x n binary matrix grid, return the length of the shortest clear path in the matrix. If there is no clear path, return -1.

A clear path in a binary matrix is a path from the top-left cell (i.e., (0, 0)) to the bottom-right cell (i.e., (n - 1, n - 1)) such that:

All the visited cells of the path are 0.
All the adjacent cells of the path are 8-directionally connected (i.e., they are different and they share an edge or a corner).
The length of a clear path is the number of visited cells of this path.

Example 1:

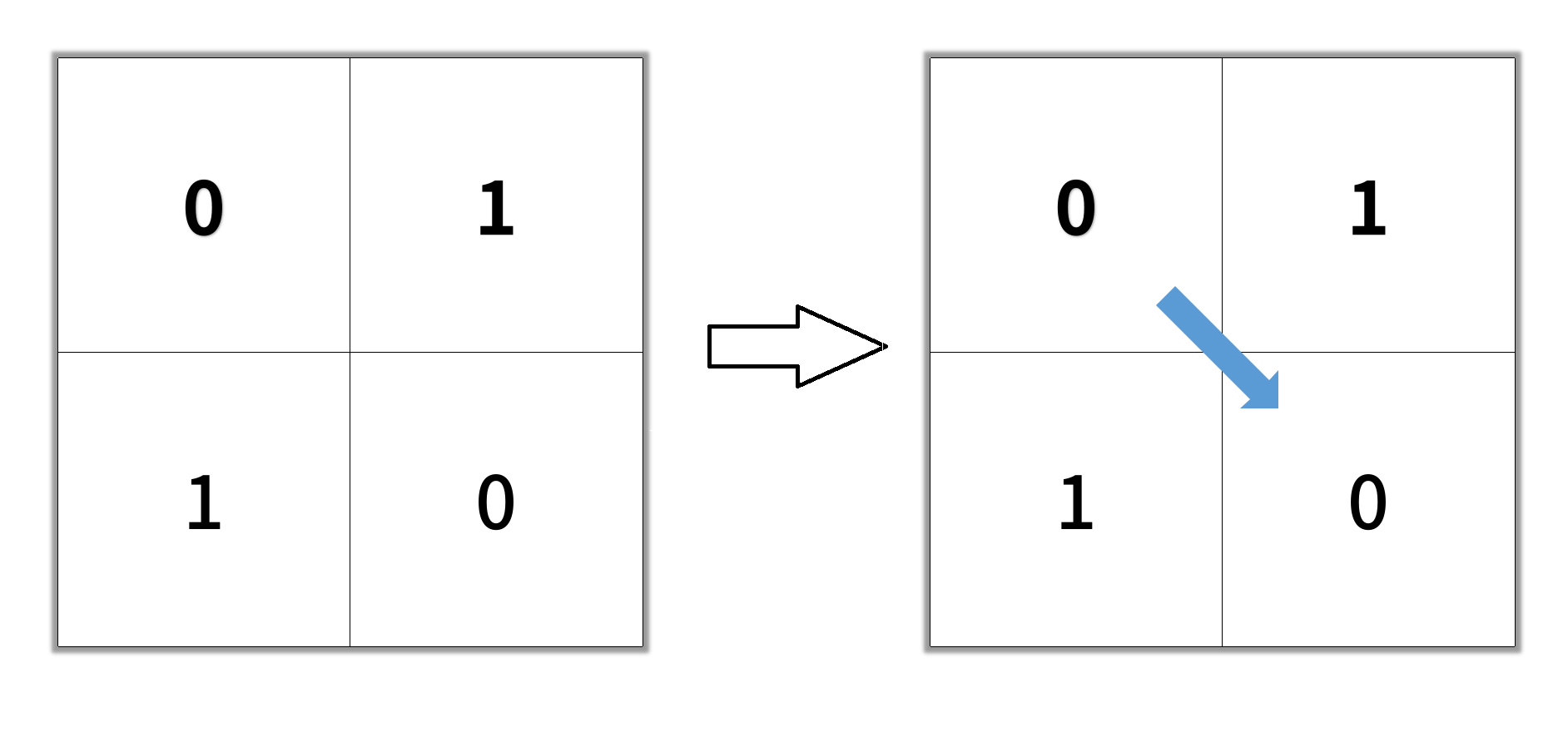
Input: grid = [[0,1],[1,0]]
Output: 2

Example 2:

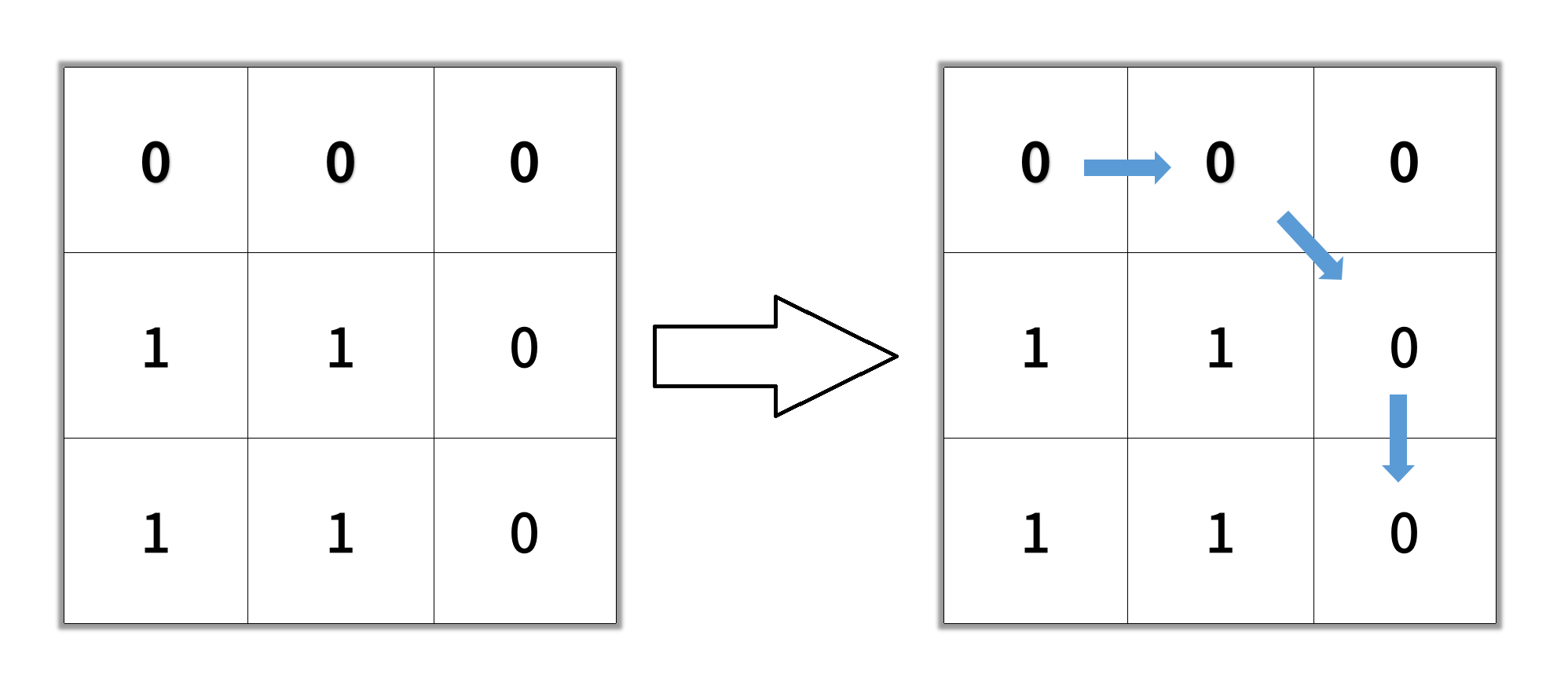
Input: grid = [[0,0,0],[1,1,0],[1,1,0]]
Output: 4

Example 3:

Input: grid = [[1,0,0],[1,1,0],[1,1,0]]
Output: -1

2. Thoughts

// Finding shortest path => Use BFS Search => Use Queue
// 1. Start with (0,0)
// 2. Get 8-directions (should do boundary check)
// 3. Should take in count of the "visited"
// 4. if reach last, return len. Else, return -1

3. Tips learned

3.1. Using Pair

std::pair stores two related values. Include to use it.

Usage:
1. Declaration:

std::pair<int, std::string> p(1, "Hello");

2. Access Elements:

std::cout << p.first << ", " << p.second << std::endl;

3. Modify Elements:

p.first = 10; 
p.second = "C++";

4. make_pair:

auto p2 = std::make_pair(2, "World");

5. Comparison:
   Pairs are compared lexicographically:

if (p1 < p2) { /* ... */ }

6. Common Use with STL Containers:
   • vector:

std::vector<std::pair<int, std::string>> vec = {{1, "A"}, {2, "B"}};

• map:

std::map<int, std::string> m = {{1, "Cat"}, {2, "Dog"}};

3.2. Using Queue

queue Overview

A queue in C++ is part of the STL and provides a FIFO (First In, First Out) data structure. Include < queue> to use it.

Usage

1. Declaration:

#include <queue>
std::queue<int> q;

2. Add Elements:
   Use push() to add elements to the back of the queue.

q.push(10);
q.push(20);
q.push(30);

3. Access Elements:
   • front() returns the first element.
   • back() returns the last element.

std::cout << "Front: " << q.front() << ", Back: " << q.back() << std::endl;

4. Remove Elements:
   Use pop() to remove the front element.

q.pop();

5. Check Size:

std::cout << "Size: " << q.size() << std::endl;

6. Check if Empty:

if (q.empty()) {
    std::cout << "Queue is empty" << std::endl;
}

Example:

#include <iostream>
#include <queue>

int main() {
    std::queue<int> q;

    q.push(10);
    q.push(20);
    q.push(30);

    std::cout << "Front: " << q.front() << ", Back: " << q.back() << std::endl;

    q.pop();
    std::cout << "After pop, Front: " << q.front() << std::endl;

    return 0;
}

3.3. Using Tuple

tuple Overview

A tuple is part of the STL (from C++11) and allows grouping multiple values of different types into a single object. Include to use it.

Usage

1. Declaration and Initialization:

#include <tuple>
std::tuple<int, std::string, double> t(1, "Hello", 3.14);

2. Access Elements:

Use std::get to access elements by index (0-based):

std::cout << std::get<0>(t) << " " << std::get<1>(t) << " " << std::get<2>(t) << std::endl;

3. Modify Elements:

std::get<1>(t) = "World";

4. make_tuple:
   Create a tuple without specifying the types:

auto t2 = std::make_tuple(42, "C++", 2.71);

5. Tie to Variables:

   Use std::tie to unpack tuple values into variables:

int a;
std::string b;
double c;
std::tie(a, b, c) = t;

6. Ignore Values:
   Use std::ignore to skip certain elements during unpacking:

std::tie(a, std::ignore, c) = t;

7. Compare Tuples:
   Tuples are compared lexicographically:

std::tuple<int, int> t1(1, 2), t2(2, 3);
if (t1 < t2) { /* ... */ }
        

8. Get Tuple Size:
   Use std::tuple_size to get the number of elements in a tuple:

std::cout << std::tuple_size<decltype(t)>::value << std::endl;

Example:

#include <iostream>
#include <tuple>

int main() {
    std::tuple<int, std::string, double> t(1, "Hello", 3.14);

    // Access and modify elements
    std::cout << "Before: " << std::get<1>(t) << std::endl;
    std::get<1>(t) = "World";
    std::cout << "After: " << std::get<1>(t) << std::endl;

    // Unpack values
    int a;
    std::string b;
    double c;
    std::tie(a, b, c) = t;

    std::cout << "Unpacked: " << a << ", " << b << ", " << c << std::endl;

    return 0;
}

3.3 Structured Binding

If you’re using C++17 or later, you can use structured bindings to unpack directly:

#include <iostream>
#include <queue>
#include <tuple>

int main() {
    std::queue<std::tuple<int, int, int>> bfs;

    bfs.push(std::make_tuple(1, 2, 3));

    // Use structured bindings to unpack
    auto [x, y, z] = bfs.front();

    std::cout << "x: " << x << ", y: " << y << ", z: " << z << std::endl;

    return 0;
}

4. My solution

#include <vector>
#include <iostream>
#include <utility>
#include <queue>
#include <tuple>

using namespace std;

class Solution
{
public:
    int shortestPathBinaryMatrix(vector<vector<int>> &grid)
    {
        int n = grid[0].size();
        if (grid.at(0).at(0) || grid.at(n - 1).at(n - 1))
            return -1;

        vector<pair<int, int>> direction = {{1, 1}, {1, 0}, {1, -1}, {0, 1}, {0, -1}, {-1, 1}, {-1, 0}, {-1, -1}};
        // row, col, length
        queue<tuple<int, int, int>> bfs;
        bfs.push({0, 0, 1});
        grid.at(0).at(0) = 1;

        while (!bfs.empty())
        {
            auto [x, y, len] = bfs.front();
            bfs.pop();
            if (x == n - 1 && y == n - 1)
                return len;
            for (auto dir : direction)
            {
                auto [dir_x, dir_y] = dir;
                int new_x = x + dir_x, new_y = y + dir_y;
                if (new_x >= 0 && new_x <= n - 1 && new_y >= 0 && new_y <= n - 1)
                {
                    if (grid.at(new_x).at(new_y) == 0)
                    {
                        grid[new_x][new_y] = 1;
                        bfs.push({new_x, new_y, len + 1});
                    }
                }
            }
        }

        return -1;
    }
};

5. AI Solution and Improvements

Your solution efficiently implements the Breadth-First Search (BFS) algorithm to solve the problem, which is optimal for finding the shortest path in an unweighted grid like this. However, there are some improvements and suggestions for better readability, efficiency, and robustness:

---

Improvements to Your Solution:

1. Early Return for Small Grid:

   • If the grid is of size 1x1 and grid[0][0] == 0, return 1 immediately.

   if (n == 1 && grid[0][0] == 0)
       return 1;

2. Avoid Copying Directions in Every Iteration:

   • Use const for the direction vector to avoid unnecessary copies.

   const vector<pair<int, int>> direction = {{1, 1}, {1, 0}, {1, -1}, {0, 1}, {0, -1}, {-1, 1}, {-1, 0}, {-1, -1}};

3. Mark the Cell While Pushing to the Queue:

   • To avoid duplicate processing, mark the cell as visited (grid[new_x][new_y] = 1) before adding it to the queue, ensuring no unnecessary checks later.

4. Simplify Bounds Check:

   • Instead of new_x >= 0 && new_x <= n - 1, simplify to new_x >= 0 && new_x < n.

5. Use a Lambda for Validity Check:

   • Encapsulate the cell validity check in a lambda function for better readability.

   auto isValid = [&](int x, int y) {
       return x >= 0 && x < n && y >= 0 && y < n && grid[x][y] == 0;
   };

6. Optimize Memory:

   • Replace the tuple with a struct or simply store the path length in the grid directly to reduce memory usage (saving len for BFS).

---

Final Improved Code:

class Solution
{
public:
    int shortestPathBinaryMatrix(vector<vector<int>> &grid)
    {
        int n = grid.size();
        if (grid[0][0] != 0 || grid[n - 1][n - 1] != 0)
            return -1;

        if (n == 1 && grid[0][0] == 0)
            return 1;

        const vector<pair<int, int>> direction = {{1, 1}, {1, 0}, {1, -1}, {0, 1}, {0, -1}, {-1, 1}, {-1, 0}, {-1, -1}};
        queue<pair<int, int>> bfs;
        bfs.push({0, 0});
        grid[0][0] = 1; // Mark as visited with the distance

        while (!bfs.empty())
        {
            auto [x, y] = bfs.front();
            int len = grid[x][y];
            bfs.pop();

            if (x == n - 1 && y == n - 1)
                return len;

            for (auto [dx, dy] : direction)
            {
                int new_x = x + dx, new_y = y + dy;
                if (new_x >= 0 && new_x < n && new_y >= 0 && new_y < n && grid[new_x][new_y] == 0)
                {
                    grid[new_x][new_y] = len + 1; // Mark visited with distance
                    bfs.push({new_x, new_y});
                }
            }
        }

        return -1;
    }
};

---

Algorithm Suggestions:

If you want to experiment with alternative approaches, consider the following:

1. A* Algorithm:

• You can use the A* algorithm to prioritize exploration towards the bottom-right corner (n-1, n-1) using a heuristic like the Manhattan Distance or Euclidean Distance.
• It may not always improve performance in terms of runtime for this problem but can reduce the number of cells visited.

Example A* Approach:

#include <queue>
#include <cmath>

class Solution
{
public:
    int shortestPathBinaryMatrix(vector<vector<int>> &grid)
    {
        int n = grid.size();
        if (grid[0][0] != 0 || grid[n - 1][n - 1] != 0)
            return -1;

        const vector<pair<int, int>> direction = {{1, 1}, {1, 0}, {1, -1}, {0, 1}, {0, -1}, {-1, 1}, {-1, 0}, {-1, -1}};
        
        auto heuristic = [&](int x, int y) {
            return sqrt((n - 1 - x) * (n - 1 - x) + (n - 1 - y) * (n - 1 - y));
        };

        priority_queue<tuple<int, int, int>, vector<tuple<int, int, int>>, greater<>> pq; // Min-heap: {f(x, y), x, y}
        pq.push({1 + heuristic(0, 0), 0, 0});
        grid[0][0] = 1;

        while (!pq.empty())
        {
            auto [f, x, y] = pq.top();
            pq.pop();

            int len = grid[x][y];
            if (x == n - 1 && y == n - 1)
                return len;

            for (auto [dx, dy] : direction)
            {
                int new_x = x + dx, new_y = y + dy;
                if (new_x >= 0 && new_x < n && new_y >= 0 && new_y < n && grid[new_x][new_y] == 0)
                {
                    grid[new_x][new_y] = len + 1;
                    pq.push({len + 1 + heuristic(new_x, new_y), new_x, new_y});
                }
            }
        }

        return -1;
    }
};

---

Comparison of BFS vs. A*:

• BFS:
  • Simpler and guaranteed to find the shortest path.
  • Explores all possible directions uniformly.
• A*:
  • Focuses on promising paths using a heuristic.
  • May reduce the number of explored cells but is slightly more complex.

When to Use:

• Stick with BFS for simple grid problems where uniform costs apply.
• Use A* when the heuristic can significantly reduce unnecessary exploration.

Your BFS implementation is efficient and well-suited for this problem, but experimenting with A* may provide valuable learning!