[LeetCode / C++] 128. Longest Consecutive Sequence

Leetcode Question Link

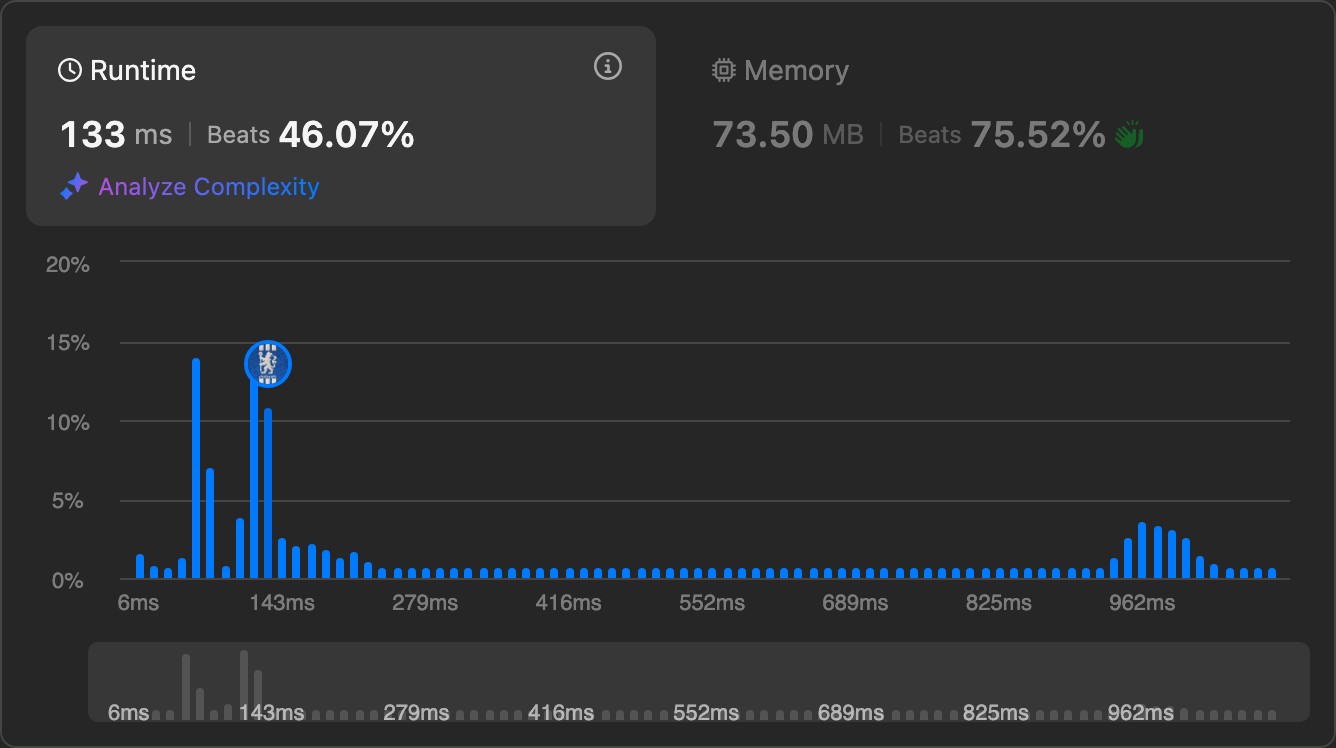
1. Question

Given an unsorted array of integers nums, return the length of the longest consecutive elements sequence.

You must write an algorithm that runs in O(n) time.

Example 1:

Input: nums = [100,4,200,1,3,2]
Output: 4
Explanation: The longest consecutive elements sequence is [1, 2, 3, 4]. Therefore its length is 4.

Example 2:

Input: nums = [0,3,7,2,5,8,4,6,0,1]
Output: 9

2. Thoughts

// Check for n-1 or n+1 if in the hashmap
// If so, add to the sequence
// else,
// for instance if we have 5,6,7 ==> (5,7) and (7,5)

// So,
//  1. Make an unordered_map
//  2. start with 1 element (if no consec. exists)
//  3. If consec exists, add to that key (check former and latter)
//  4. if both former and latter exists, concat the two consecutives

// ex) n= 5 => if we have 6,7,8 => (5,8) // (8,5)
// ex2) n =5, we have 2,3,4 => (2,5) // (5,2)
// ex3) n =5, we have 2,3,4 & 6,7,8 => (2,8) (8,2)

3. Tips learned

4. My solution

class Solution
{
public:
    int longestConsecutive(vector<int> &nums)
    {
        if (!nums.size())
            return 0;

        unordered_map<int, int> hashmap;
        for (int i = 0; i < nums.size(); i++)
        {
            int n = nums.at(i);

            // duplicate
            if (hashmap.find(n) != hashmap.end())
                continue;

            // one below && one over both exists => concat the consecutives.
            if (hashmap.find(n + 1) != hashmap.end() && hashmap.find(n - 1) != hashmap.end())
            {
                int new_start = min({n - 1, hashmap[n - 1], hashmap[n + 1]});
                int new_end = max({n + 1, hashmap[n - 1], hashmap[n + 1]});
                hashmap.erase(hashmap[n - 1]);
                hashmap.erase(hashmap[n + 1]);
                hashmap.erase(n - 1);
                hashmap.erase(n + 1);
                hashmap[new_start] = new_end;
                hashmap[new_end] = new_start;
            }

            // exists one below // ex) n= 5 => if we have 6,7,8
            else if (hashmap.find(n + 1) != hashmap.end() && hashmap[n + 1] >= n + 1)
            {
                int start = n + 1, end = hashmap[n + 1], new_start = n;
                hashmap.erase(start);
                hashmap[new_start] = end;
                hashmap[end] = new_start;
            }
            // ex2) n =5, we have 2,3,4 => (2,3) // (4,2)
            else if (hashmap.find(n - 1) != hashmap.end() && hashmap[n - 1] <= n - 1)
            {
                int start = hashmap[n - 1], end = n - 1, new_end = n;
                hashmap.erase(end);
                hashmap[start] = new_end;
                hashmap[new_end] = start;
            }

            // no latter or former
            else
            {
                hashmap[n] = n;
            }
        }

        int max_result = 0;
        for (auto x : hashmap)
        {
            max_result = max(max_result, x.first - x.second);
        }

        return max_result + 1;
    }
};

5. AI Solution and Improvements

Your current approach is designed to track the start and end of each consecutive sequence using a hash map, which is creative but a bit complex and may be improved in terms of readability and efficiency.

A more optimal approach is to use a unordered_set to eliminate duplicates and then iterate through the set only when an element is the start of a sequence. Here’s the improved algorithm:

Explanation of the Improved Algorithm

1. Insert all elements into an unordered_set, which allows O(1) average-time complexity for lookups.
2. Iterate through the elements of the set. For each element:
   • Check if it is the start of a sequence by seeing if num - 1 is not in the set. If it is, skip to the next element since it’s part of an already counted sequence.
   • If it’s the start of a sequence, count the length of the sequence by iterating while num + length exists in the set.
3. Track the maximum length of any sequence found.

This approach is efficient because each element is only visited once in the main loop, resulting in O(n) time complexity.

Improved Code

class Solution {
public:
    int longestConsecutive(vector<int>& nums) {
        unordered_set<int> num_set(nums.begin(), nums.end());
        int longest_streak = 0;

        for (int num : num_set) {
            // Only start counting if `num` is the beginning of a sequence
            if (num_set.find(num - 1) == num_set.end()) {
                int current_num = num;
                int current_streak = 1;

                // Count the length of the sequence starting at `num`
                while (num_set.find(current_num + 1) != num_set.end()) {
                    current_num += 1;
                    current_streak += 1;
                }

                // Update the maximum streak length
                longest_streak = max(longest_streak, current_streak);
            }
        }

        return longest_streak;
    }
};

Explanation of Changes

• Use of unordered_set: This avoids duplicate elements and allows O(1) lookups.
• Simplified logic: Instead of keeping track of both ends of sequences in a hashmap, we identify the start of each sequence and count its length until it ends. This reduces complexity and avoids extensive hash map operations.
• Efficiency: The algorithm is now more concise and straightforward, with O(n) time complexity, since we only iterate through the set once and do a linear scan for each sequence start.

This code is easier to understand, and the performance is optimized by reducing unnecessary operations, achieving the required O(n) complexity.