[SW Expert Academy] 1249. Supply Route

1. Question

As World War II intensifies, battles between the Allies and German forces are becoming increasingly fierce.

The area where the fighting is taking place has roads damaged due to extensive bombing and urban warfare, making it impassable for vehicles like trucks or tanks, as illustrated in Figure 1(a).

For victory in battle, it is essential to have roads for the rapid movement of armored divisions and supply units.

The engineering corps aims to complete road repair work as quickly as possible from the starting point (S) to the destination (G).

The repair time increases in proportion to the depth of the damage on the roads.

Find the total repair time for the shortest path from the starting point to the destination, assuming the repair time is 1 for a depth of 1.

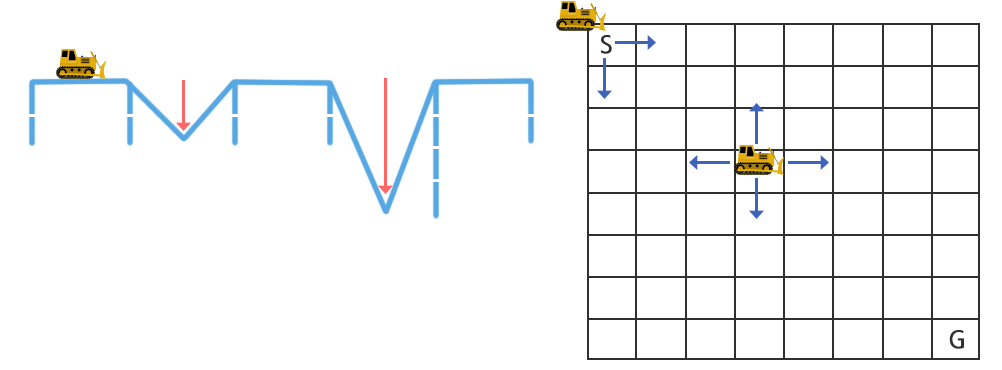
The map information is displayed in a 2D array format as shown in Figure 1(b), with the starting point at the top left corner (S) and the destination at the bottom right corner (G).

The path can move in up, down, left, or right directions, moving one cell at a time.

The map information includes the depth of damage on each cell's road. The road on the current cell must be repaired to move to another location.

Assume that the time to move is negligible compared to the time needed for repair.

Therefore, the distance from the starting point to the destination does not need to be considered.

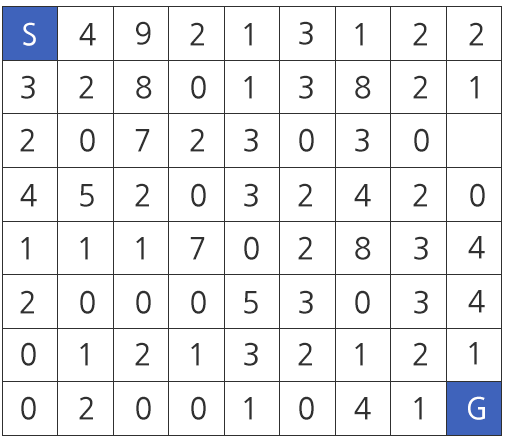
The map information is in the form of a 2D array, as shown in Figure 2, with the starting point (S) and destination (G) located at the top left and bottom right corners, respectively, and represented as 0 in the input data.

Places other than the starting and destination points that are marked as 0 do not require repair work.

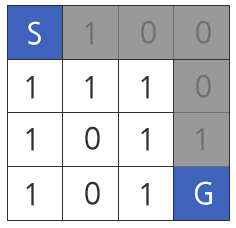
In the given map, the minimum repair work time is 2, and the path is highlighted in gray.

2. Thoughts

1. Use Dijsktra algorithm

3. Tips learned

3.1. Dijkstra Algorithm

1. Dijkstra Algorithm in Python
2. Dijkstra Algorithm in Python II

3.2. Defining 2D array in python

The output of

   distance = [[float("inf")] * size] * size
   print(distance)
   distance[0][0] = 0
   print(distance)

was weirdly

[[inf, inf, inf, inf], [inf, inf, inf, inf], [inf, inf, inf, inf], [inf, inf, inf, inf]]
[[0, inf, inf, inf], [0, inf, inf, inf], [0, inf, inf, inf], [0, inf, inf, inf]]

This was due to how 2D arrays are initialized in your code snippet. When you use:

distance = [[float("inf")] * size] * size

You're creating a list of size lists, but each of those lists is actually a reference to the same list in memory. This means that when you modify one row (in your case, distance[0][0] = 0), it appears as though you've modified the same index in all rows, because all rows are referencing the same single list.

To create a 2D array where each row is an independent list (so modifying one row doesn't affect the others), you should use a list comprehension or a similar method that ensures each row is a separate list object, like this:

distance = [[float("inf")] * size for _ in range(size)]

With this approach, distance[0][0] = 0 will modify only the first element of the first row, as you initially expected, resulting in:

[[0, inf, inf, inf], [inf, inf, inf, inf], [inf, inf, inf, inf], [inf, inf, inf, inf]]

This occurs because the list comprehension creates a new list [float("inf")] * size for each iteration of the loop, resulting in size independent lists (rows) within your 2D array.

4. My solution

import sys
from heapq import *

sys.stdin = open("input.txt", "r")


T = int(input())

for test_case in range(1, T + 1):
    size = int(input())
    table = []
    distance = [[float("inf")] * size for _ in range(size)]
    directions = [(0, 1), (0, -1), (1, 0), (-1, 0)]

    ans = 0

    for _ in range(size):
        row_input = input()
        row = [int(char) for char in row_input]
        table.append(row)

    distance[0][0] = 0
    queue = [(table[0][0], 0, 0)]

    while queue:
        repair_time, row, col = heappop(queue)
        if row == size - 1 and col == size - 1:
            ans = repair_time
            break
        for add_row, add_col in directions:
            next_row, next_col = row + add_row, col + add_col
            if 0 <= next_row < size and 0 <= next_col < size:
                new_time = repair_time + table[next_row][next_col]

                if new_time < distance[next_row][next_col]:
                    distance[next_row][next_col] = new_time
                    heappush(queue, (new_time, next_row, next_col))

    print(f"#{test_case} {ans}")

5. AI Solution and Improvements

Your solution is already well-structured and makes good use of Dijkstra's algorithm for finding the shortest path in terms of repair time on a 2D grid. However, there are a few optimizations and improvements you can consider:

1. Early Stopping Condition: You already have an early stopping condition when you reach the destination (size - 1, size - 1). This is efficient and should be kept as is.

2. Initial Queue Setup: You initialize the queue with (table[0][0], 0, 0), but since you set distance[0][0] = 0, you should push (0, 0, 0) to the queue to correctly represent the starting condition. This ensures the initial state reflects that there's no repair time needed to start from the first cell if you're considering the starting point as having no depth. If the starting point also requires repair, then your current initialization is correct.

3. Input Reading: Your input reading method is efficient for the given problem. However, if you're looking to further optimize or make the code cleaner, Python's list comprehension is already doing a good job. Ensure that using sys.stdin and input.txt is suitable for your environment; this is good for competitive programming or if you're running scripts locally but might need adjustment for different contexts.

4. Heap Optimization: The way you're using the priority queue is optimal for Dijkstra's algorithm. Just ensure that the comparison of tuples in the priority queue doesn't lead to unexpected behavior. Python's heapq compares tuples element-wise, starting with the first element, which suits your current implementation.

5. Variable Naming and Comments: While your variable names are clear, adding comments to explain critical sections of your code, especially the logic inside the loop, can improve readability and maintainability.

6. Optimizing Distance Update: You are checking if new_time < distance[next_row][next_col] before pushing to the queue. This is correct and ensures that only promising paths are explored. No further optimization is needed here without changing the algorithmic approach.

7. Error Handling and Validation: Depending on the source of your input, it might be worth adding validation for the input data, especially the sizes and values of the table, to ensure they meet the expected format and constraints.

Given these points, your code is quite optimized for the problem statement. The primary improvement lies in ensuring the initial conditions and inputs are correctly set up, and the early stopping condition is effectively utilized. Adding comments for clarity and ensuring your code handles different input sources correctly can also be beneficial.