
ch04 Edit distance
Edit Distance?

Edit Distance는 두 문자열 사이의 유사성을 측정하는 방법으로, 한 문자열을 다른 문자열로 바꾸는 데 필요한 최소한의 편집 연산(editing operations)의 수를 의미함.
편집 연산의 종류는 크게 세 가지:
- 삽입(Insertion)
- 삭제(Deletion)
- 대체(Substitution)
예시로 "Intention"이라는 단어를 "Execution"으로 바꿀 때 최소한의 편집 연산을 계산하고, 이를 통해 최적의 alignment를 찾을 수 있음.
응용 분야

단어뿐 아니라 문장이나 구(phrase) 수준에서도 사용 가능하며,
특정 문장을 다른 문장으로 변형하기 위한 최소 연산 횟수를 구할 수 있음.
- Named Entity Extraction(개체명인식)
- Entity Coreference에서도 자주 활용
- 기계 번역(Machine Translation)의 성능 평가에도 사용됨
Minimum Edit Distance

최소 edit distance를 찾는 문제는 본질적으로 초기 상태(initial state)에서 목표 상태(goal state)까지의 최적 경로(optimal path)를 찾는 문제로 이해할 수 있음.
-> 상태 공간 탐색(Search space) 문제로 접근
- 초기 상태(initial state): 변형할 원본 단어
- operators: 삽입, 삭제, 대체
- Goal state: 도달하고자 하는 문자열
- Path cost: 편집 횟수(최소화할 대상)
- 미니멈 패스 코스트는 각 값을 저장하는 테이블의 마지막 값을 의미
이 문제를 무작정 탐색하면 모든 가능한 문자열 변환을 다 시도해야 하므로 비효율적임. 대신, 효율적이고 최적화된 방법을 사용해야 함.
Edit Distance 의 공식 정의

두 문자열 X, Y가 있을 때 각각의 길이를 |X|=n, |Y|=m이라 하자.
D(i,j)를 문자열X[1,...,i]를 문자열Y[1,...,j]로 바꾸는 데 필요한 최소 편집 거리라고 정의함.- 최종적으로 두 문자열 간의 편집 거리는
D(n,m)이 됨.
Min Edit Distance 계산 방법 (Dynamic Programming)

최소 편집 거리는 동적 프로그래밍으로 효율적으로 해결 가능함.
- 중간 결과(intermediate output)를 테이블 형태로 저장함.
- 특정 문자열이 다른 문자열로 가는 최적 경로상에 있으면, 이전에 계산된 최적 경로를 이용할 수 있음(최적 부분 구조).
- 점화식을 이용하여 하위 문제(subproblem)를 해결한 후 상위 문제로 결합하는 bottom-up 방식을 사용
- 작은 값의
D(i,j)를 먼저 계산 - 이를 바탕으로 큰 값의
D(i,j)를 계산 - 모든
0 < i ≤ n,0 < j ≤ m인D(i,j)를 계산
- 작은 값의

- initialization : 테이블의 초기화 (중요)
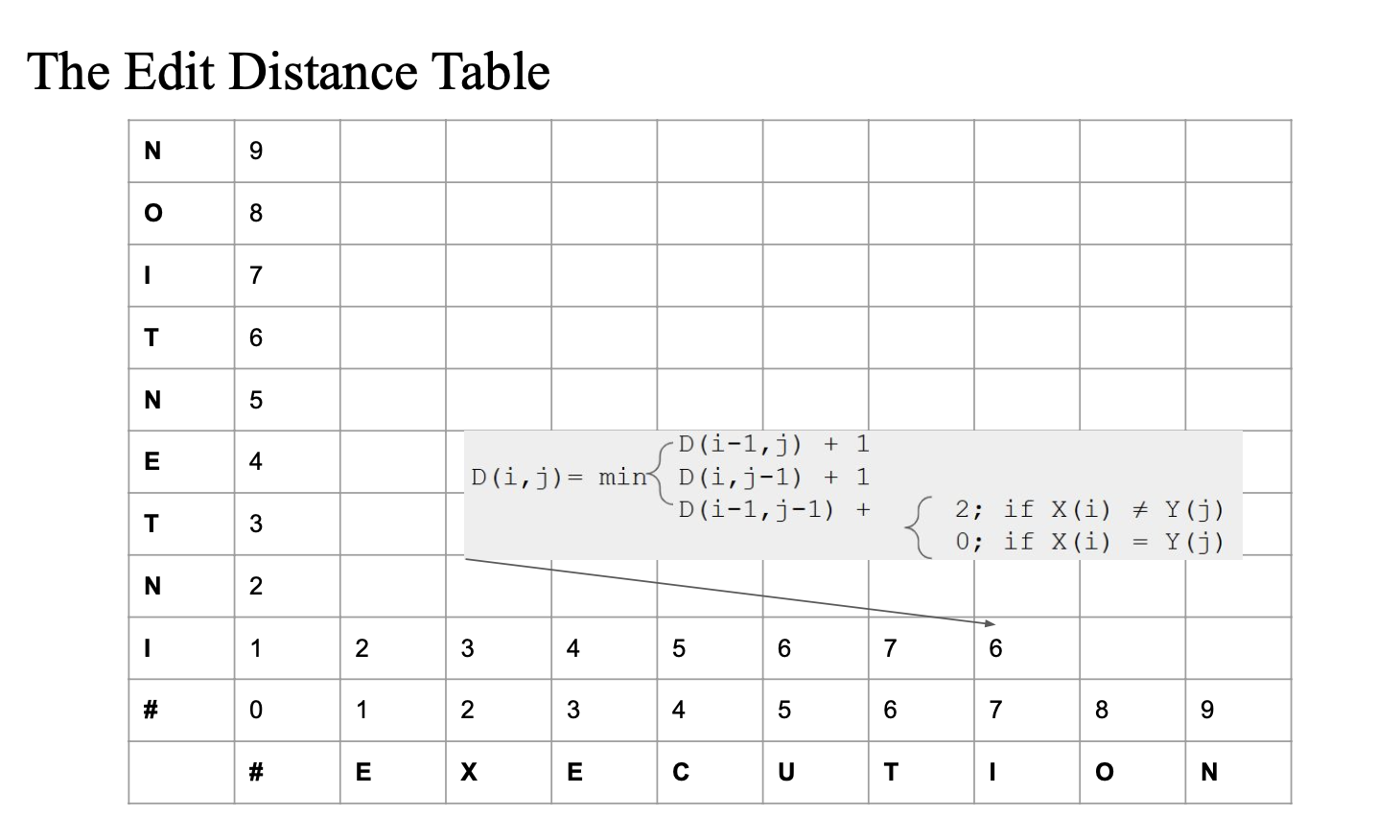
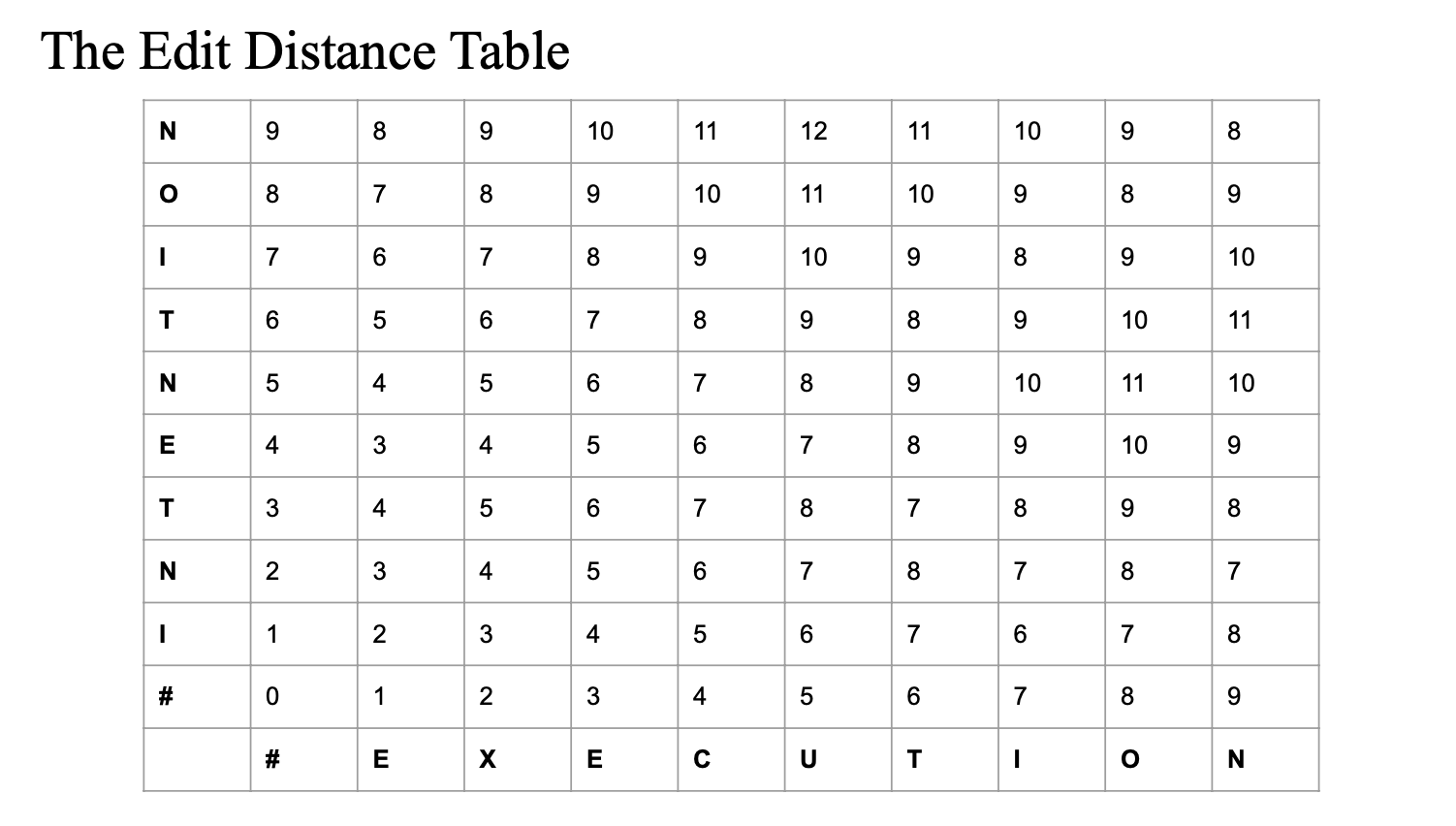
Edit distance table 구성하기
 |  |
|---|
편집 거리 문제를 동적 프로그래밍으로 해결하려면 테이블 형태로 각 단계에서 계산한 값을 저장해야 함.
- 가로축은 목표 문자열("EXECUTION")이고, 세로축은 원본 문자열("INTENTION")임.
- 각 칸
D(i,j)는 원본 문자열의 처음부터 i번째 문자까지와 목표 문자열의 처음부터 j번째 문자까지 간의 최소 편집 거리를 나타냄. - 최종적으로 우측 상단에 있는 값이 두 문자열 전체 간의 최소 편집 거리임.
- D(i,0)은 원본 문자열의 처음 i개의 문자를 빈 문자열로 만드는 비용으로, 즉 모두 삭제하는 비용이므로 값은 i
- D(0,j)는 빈 문자열을 목표 문자열의 처음 j개 문자로 바꾸는 비용으로, 즉 모두 삽입하는 비용이므로 값은 j
역추적(Backtrace)을 통한 정렬 찾기

테이블을 완성하면 최소 편집 거리를 구했지만, 어떤 연산을 했는지는 바로 알 수 없음. 이때 역추적(backtrace)을 통해 실제 수행한 연산을 찾음.
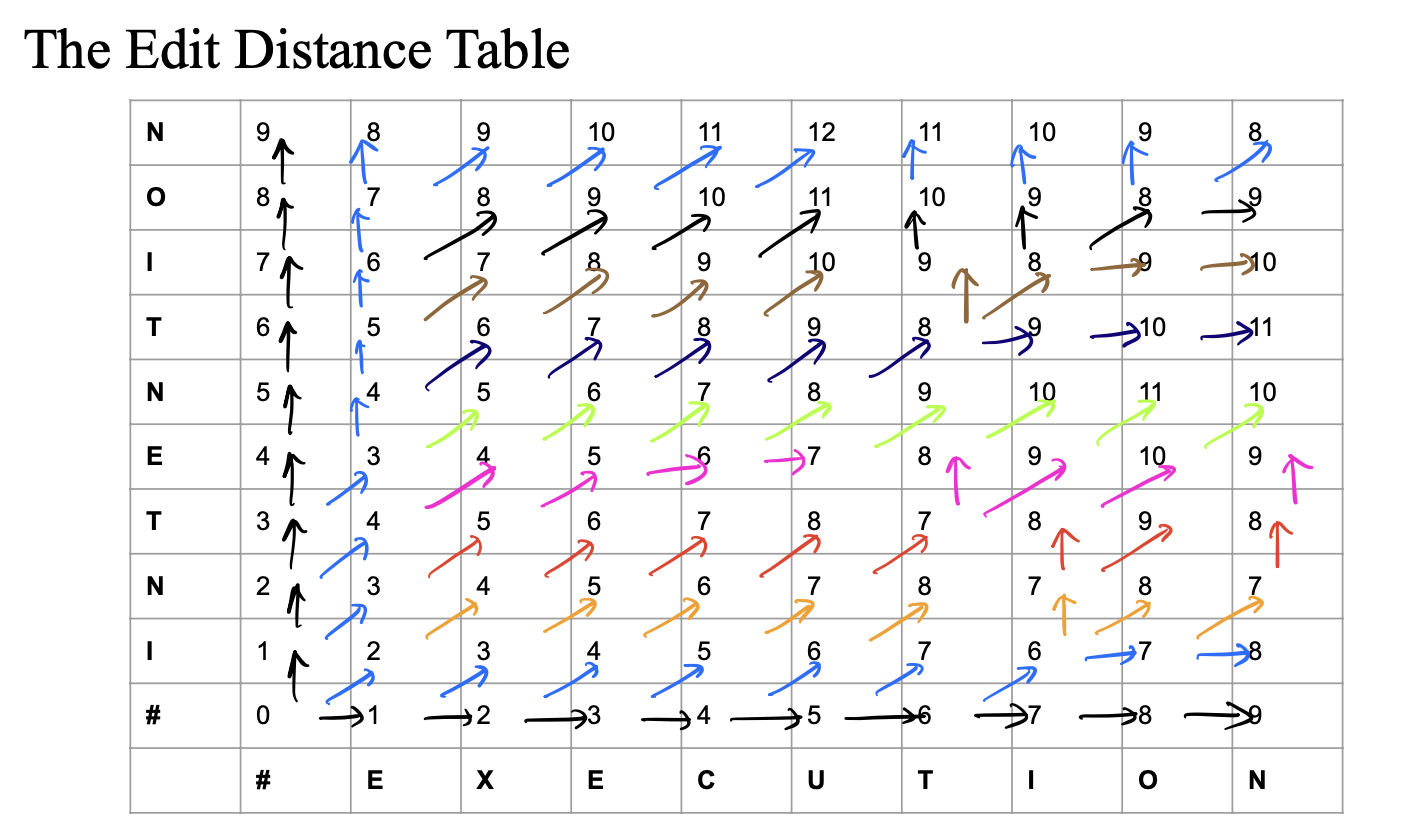
역추적 방법
- 테이블을 채울 때 각 칸에서 어떤 방향에서 왔는지를 기록해 둠.
- 이때 가능한 방향은 다음 세 가지임:
- 위쪽에서 왔다면(↓): 삭제 연산 (Deletion)
- 왼쪽에서 왔다면(→): 삽입 연산 (Insertion)
- 왼쪽 위 대각선에서 왔다면(↘︎): 치환 연산(Substitution) 혹은 동일 문자(연산 필요 없음)
테이블이 모두 채워지면 우측 상단에서 시작해 왼쪽 아래로 이동하면서 역추적을 진행함. 이 과정에서 실제 사용된 연산이 나타남.
백트래킹이 중요..
->백 트래킹을 통해 나온 결과를 통해 어떤 오퍼레이션이 적용됐는지 확인이 가능하다..
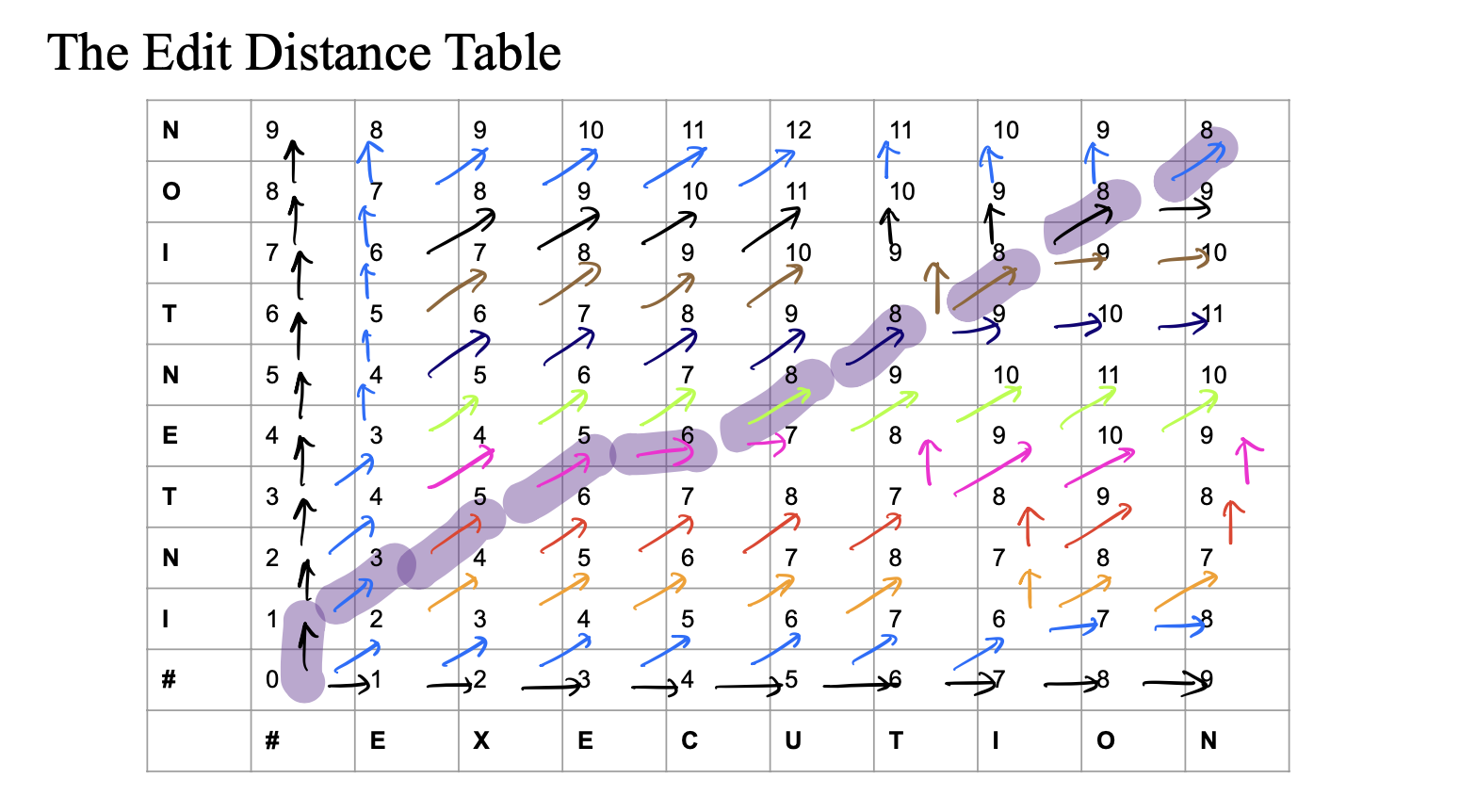
실제 역추적 예시 (INTENTION → EXECUTION)
 |  |
|---|
테이블 우측 상단에서 출발하여 각 단계에서 기록된 방향을 따라 이동함.
- 이동 경로를 따라가면서 선택된 연산(삽입, 삭제, 치환)을 확인할 수 있음.
- 이렇게 얻은 최적의 이동 경로가 최소 편집 거리를 실현하는 연산 순서가 됨.
역추적 공식

이 과정을 통해 각 셀마다 최소 비용이 계산되며, 최종적으로 두 문자열 전체 간의 최소 비용이 완성됨.
