
ch05 Hidden Markov Models (ForwardProbabilities, Viterbi Algorithm)
Sequence Labeling

- 많은 NLP 문제는 시퀀스 레이블링 작업으로 볼 수 있음.
- 시퀀스 내 다른 아이템들의 레이블을 기반으로 다음 아이템의 레이블 찾기
- 개체명 인식(Named Entity Recognition), 의미역 결정(Semantic Role Labeling) 등..

근데 이제 자연어 처리 문제는 단순한 개별 분류 문제와 달라서, 요소들(단어, 구절 등) 간의 관계와 순서, 의존성을 고려하는 특별한 접근 방식(학습 및 추론 방법)이 필요함..
일반적인 분류 문제는 각 데이터(사례, case)를 독립적으로 취급..
즉, 하나의 데이터를 분류하는 결정이 다른 데이터의 분류에 영향을 미치지 않는다고 가정합니다.
(스팸 메일 분류 시, 한 메일이 스팸인지 아닌지 판단하는 것은 다른 메일의 판단과 무관하다고 보는 것)
-> 근데 사실 언어는 여러가지 의미들이 주변 단어들에게 영향을 받음 -> 의존적... 의존성이 있음..
-> 이전 결과를 다음 결과에 영향을 주는 것..
-> dependency 를 인코딩 하기 위해 hmm 을 이용..
-> 새로운 기법 필요..
확률적 시퀀스 모델(Probabilistic Sequence Models)

여러 개의 서로 종속적인 분류 문제를 한 번에 처리할 때 단순히 개별적으로 독립적인 모델을 사용하는 것이 아니라, 전체적으로 가장 가능성 높은(global assignment) 결과를 결정하는 모델을 쓰는 것
- Hidden Markov Models (HMM)
- 관측 가능한 값(observation)을 통해 숨겨진 상태(hidden state)의 시퀀스를 확률적으로 추론함.
- 주로 품사 태깅, 음성 인식 등의 시퀀스 예측(sequence labeling)
- Conditional Random Fields (CRF)
- 주어진 관측 시퀀스에 조건부로 숨겨진 상태 시퀀스를 모델링하는 확률적 방법으로, 구조적 예측에 자주 쓰임.
- 주로 개체명 인식(NER), 시맨틱 역할 표기(Semantic Role Labeling)
Hidden Markov Models (HMM)

자연어 처리(NLP)에서는 문장이나 텍스트를 다룰 때, 각 단어들이 독립적으로 존재하지 않고 서로 긴밀히 연결된 형태로 나타나는 경우가 많음. 이를 효과적으로 모델링할 수 있는 방법 중 하나가 바로
Hidden Markov Model(HMM)
HMM의 기본 개념
HMM은
숨겨진 상태(hidden states)와 관측값(observations) 사이의 관계를 확률적으로 모델링하는 방식임.
- 숨겨진 상태 (Hidden States)
- 직접 관측되지 않고 추론을 통해서만 알 수 있는 상태를 의미함.
- 관측값 (Observations)
- 실제로 데이터를 통해 직접 볼 수 있는 값들임. HMM은 이 관측값으로부터 숨겨진 상태를 추정함.
왜 "Hidden" 인가?
- 상태(State) 자체는 직접 볼 수 없고, 관측값(observation)을 통해서 간접적으로 상태를 추론하기 때문에 hidden이라고 표현함.
- 예를 들어, 문장에서 각 단어는 관측값이며, 단어의 문법적 역할(품사)은 숨겨진 상태로 볼 수 있음.
Markov Model
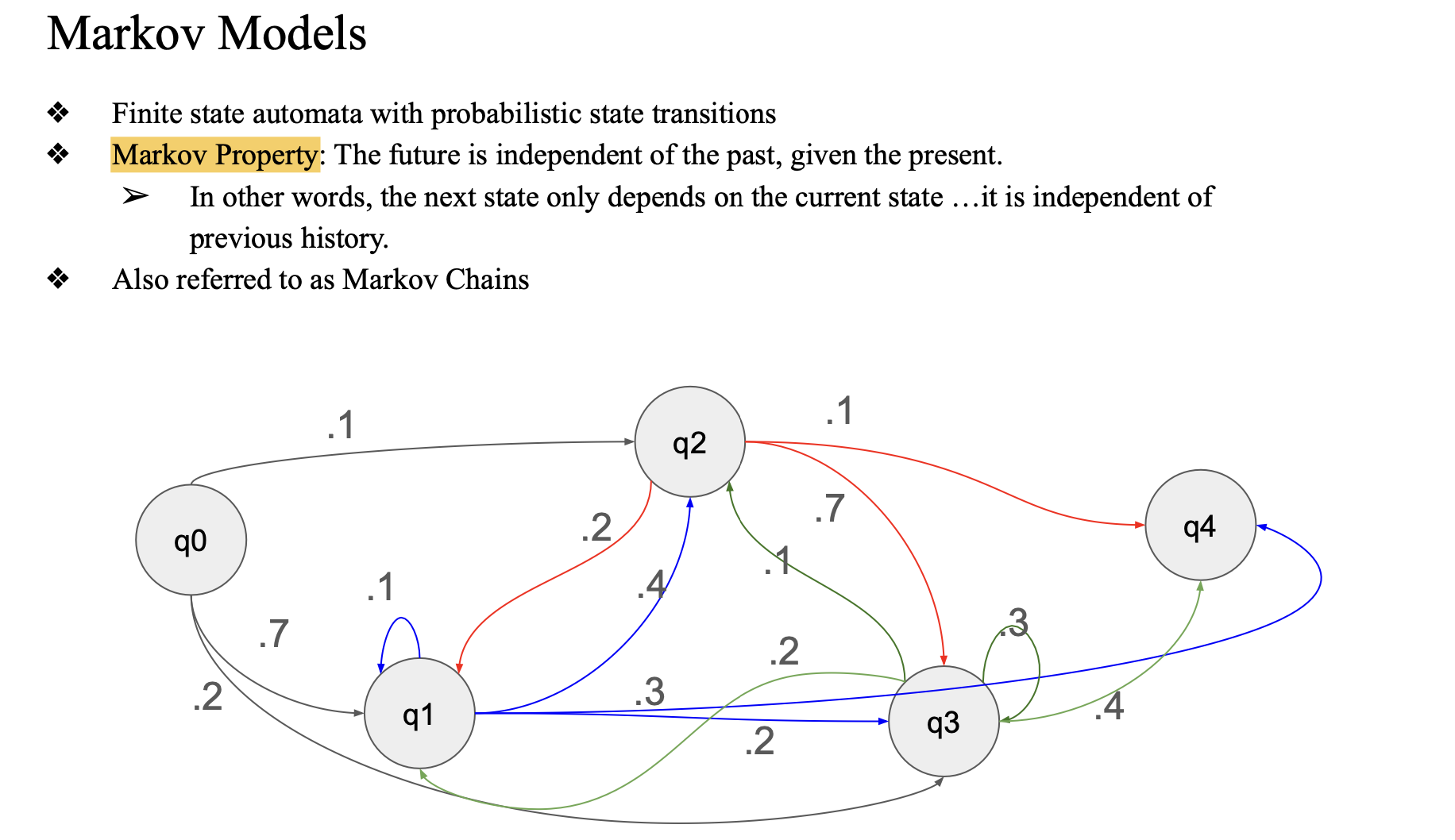
HMM은 마르코프 모델에 기반을 두고 있음. 마르코프 모델은 현재 상태에서 다음 상태로 넘어가는 확률을 정의하는 모델임.
마르코프 property 를 기반으로 함..
- Markov Property
- 미래 상태가 현재 상태에만 의존하고 과거 상태와는 무관하다는 속성임.
- 즉, 다음 상태로의 전이는 현재 상태에만 의존함.
- 직전 상태만 영향..
마르코프 모델은 확률적 상태 전이(Probabilistic State Transitions)를 나타내며, 상태 간의 이동이 확률로 표현됨.
-> FSA에 probability가 붙은 형태
sample
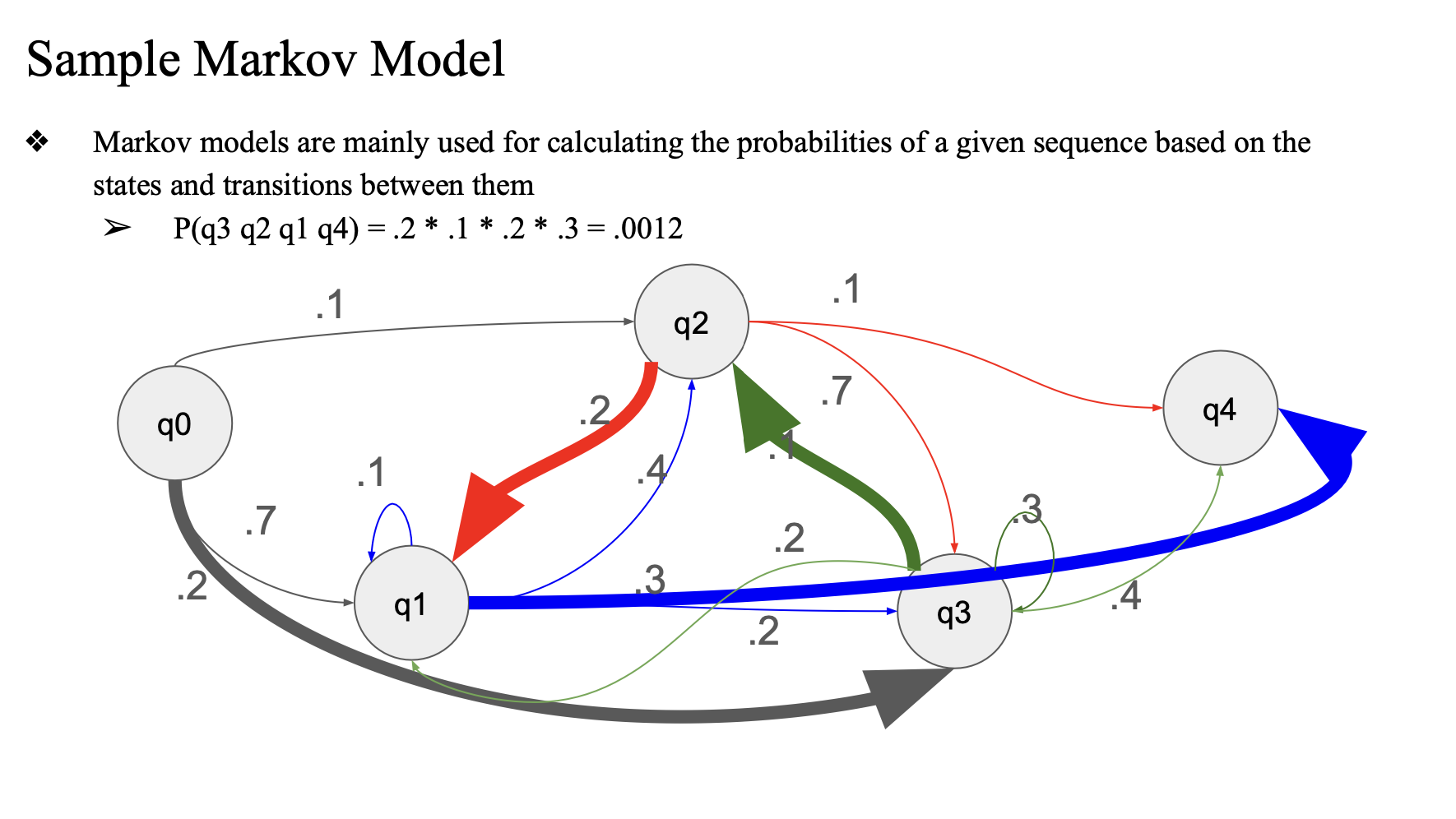
- 만약에 q2가 현재 상태이고 이 상태가 q0 -> q1 -> q2 라면,
- q2를 계산하기 위해서 q0, q1 을 모두 고려해야됨
- 하지만 q1에서만 오는 확률로만 q2의 확률을 계산한다..
q3 q2 q1 q4의 시퀀스에서의 확률, P(q3 q2 q1 q4) = 0.0012 라고 할때
markov model 을 쓸 수 있다.
HMM

hidden state가 실생활에서 추론하기 어려운 것이므로 hmm을 사용해서 추론하는 것
- hidden states
- transition probabilities
- observation probabilities
예시
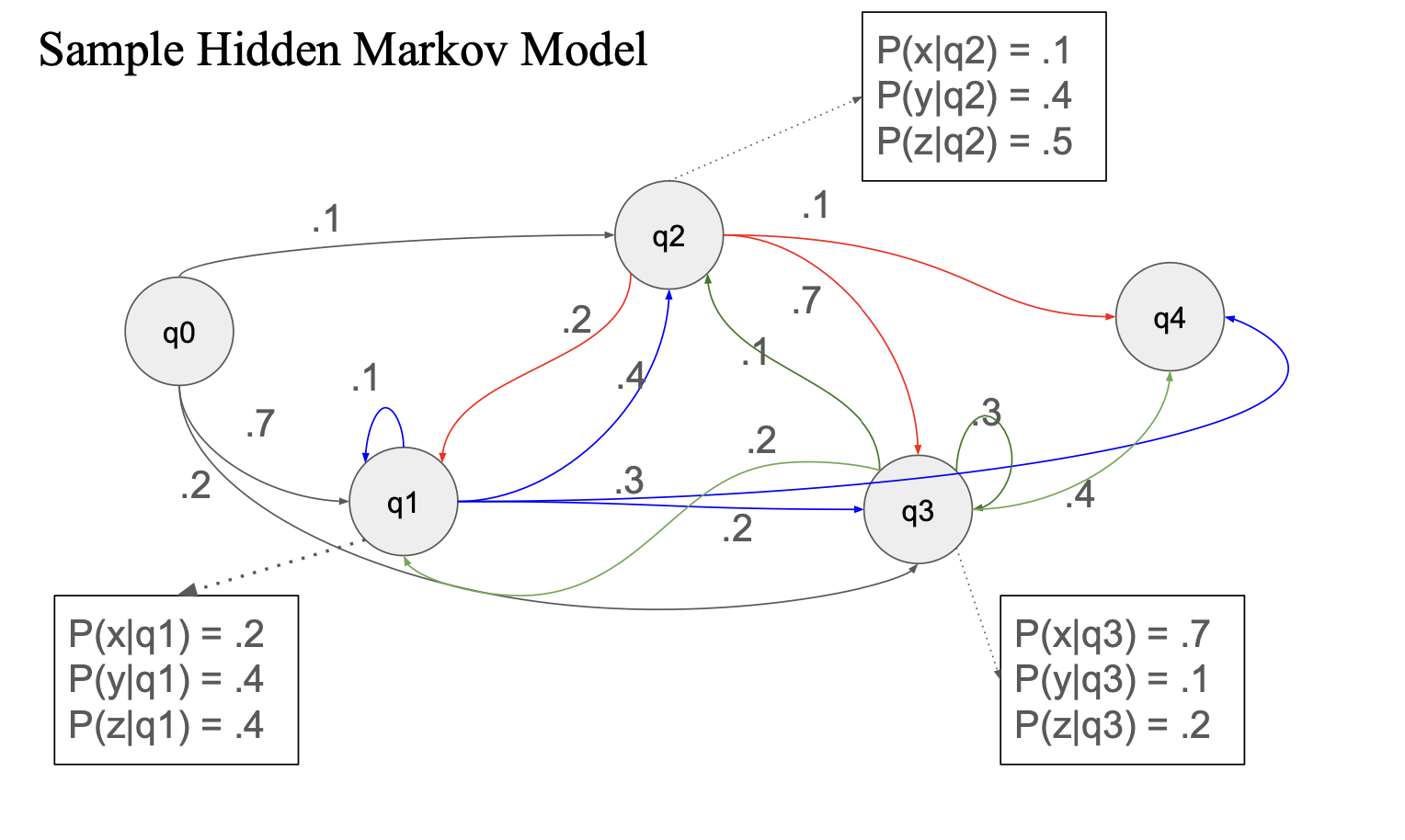
q0 : start state
q4 : finiite state
여러 state 가 존재하고 각각의 state 사이에 transition probability 존재,
그리고 각각의 state 별로 emission probability 존재
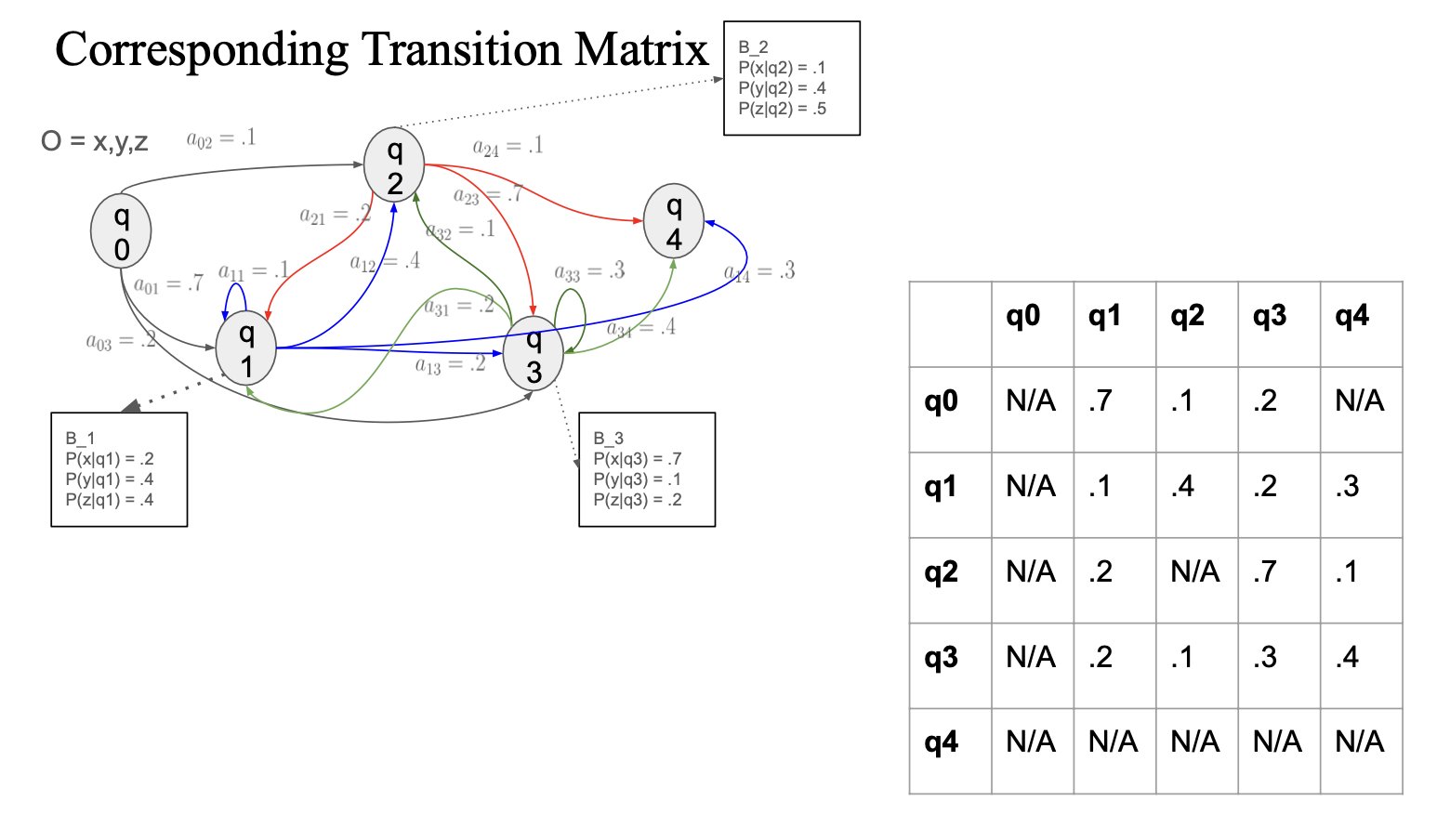
Formal Definition

Hidden Markov Model을 정의하려면 다음 요소들이 필요함.
- 상태 집합(Q)
- 모델이 가질 수 있는 가능한 숨겨진 상태들의 집합.
- 상태 전이 확률 행렬 (A)
- 특정 상태에서 다른 상태로 전이할 확률을 나타내는 행렬.
- 예시: (a_{ij})는 상태 (i)에서 상태 (j)로 이동할 확률임. 모든 (i)에 대해 합이 1이 됨.
- 관측값 확률 분포 (B) - Emission Probability
- 특정 상태에서 관측값이 나타날 확률을 나타냄.
- 예시: 특정 상태 (i)에서 관측값 (o_t)가 나타날 확률.
- 초기 상태 확률 (π)
- 초기 상태로 시작할 확률을 나타냄.
observation likelihood이 아니라 emission probability 라고 하는 게 맞음
(likelihood 와 probability 의 차이는 나중에 다룰 예정)
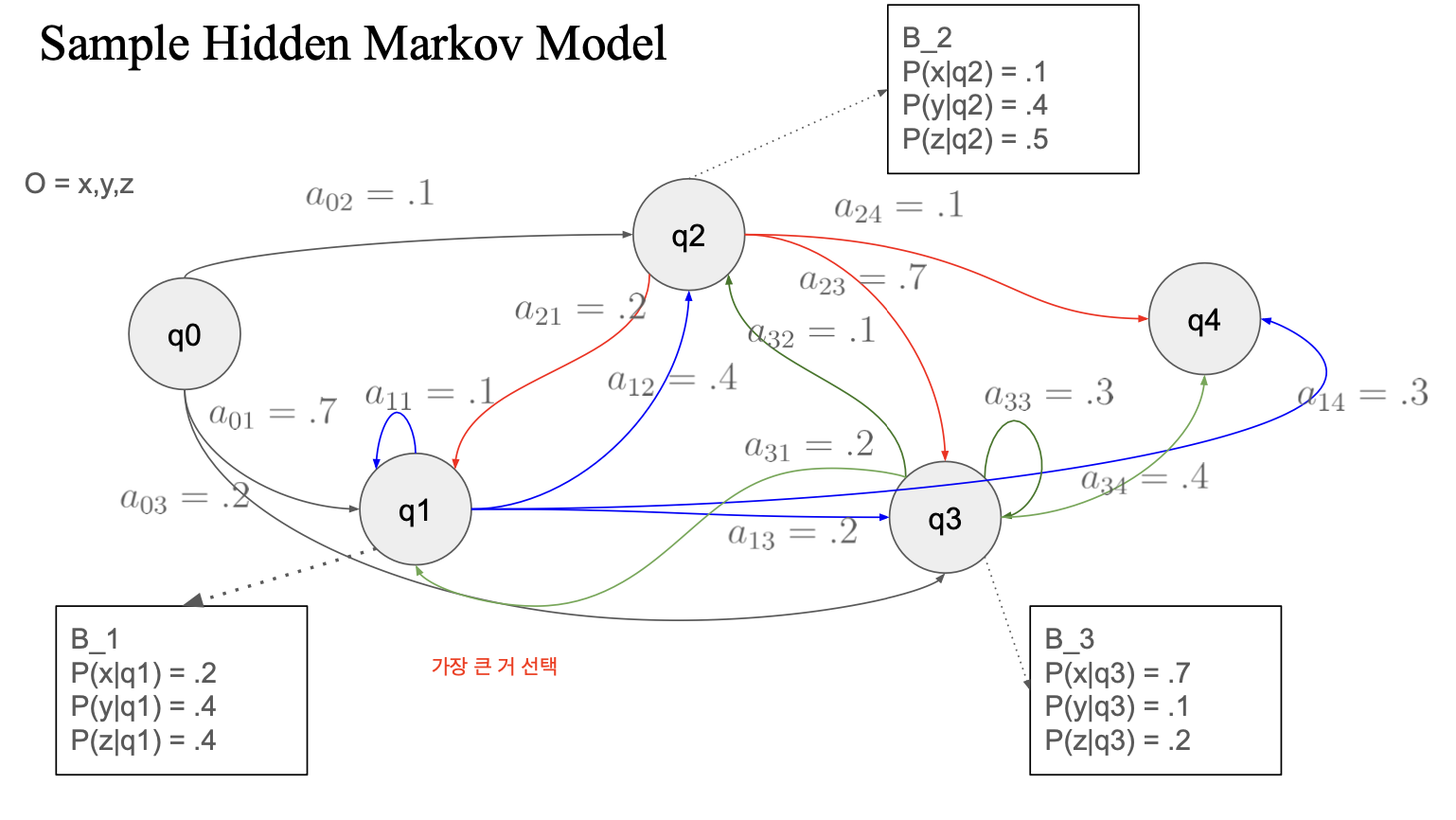
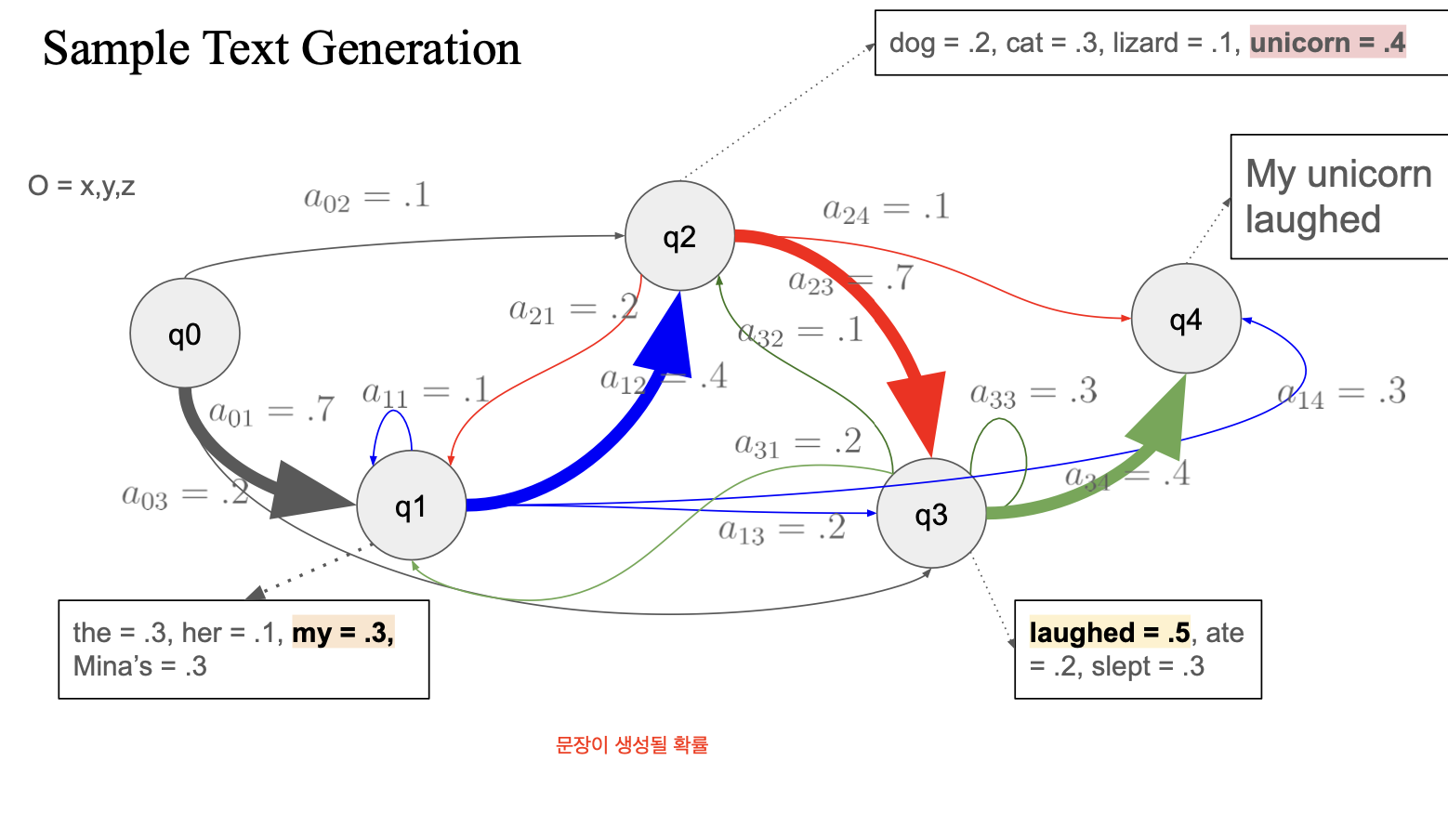
- q0에서 랜덤하게 픽 (가장 큰 확률이 픽될 확률이 큼)
- a01 을 선택해서 q1 으로 가서
- q1의 emission prob 중 my를 선택
- 갈 수 있는 state 중 가장 큰 확률 선택
-> q2 로 이동
- 갈 수 있는 state 중 가장 큰 확률 선택
- q2에서 0.4 인 unicorn 선택
-> my + unicorn
- 또 다음 state 이동 (0.7, q3)
- q3에서 laughed 선택
=> my + unicorn + laughed
- q3에서 laughed 선택
- 또 다음 state 이동(0.4, q4)
- q4에는 emission prob 없음
그러면 이제 generation 하면 됨
최종 출력: "My unicorn laughed"
Three Fundamental HMM Problems

observation Likelihood: How likely is a particular observation sequence to occur?
- 어떤 observation 에 대해서 확률을 구하기
- 주어진 문장을 보고 -> state들을 추론 -> sequence를 알아내는 과정
- 품사,,나 문맥 정보를 hidden state로 모델링 할 수도 있음
- 품사가 어떻게 tagging 될 수 있느냐..
- 이 모든 과정 (q0~q4의 시퀀스를 추론해내는 과정) -> decoding
Decoding: What is the best sequence of hidden states for an observed sequence? - 비터비 알고리즘 vs forward : 비슷
- 차이는 결국 backtracking
- 화살표가 각각 어디에서 온 건지...의 정보를 저장해놓기만 하면 hidden state를 추적할수잇는데....
- 어떤 디코딩 알고리즘을 쓰느냐에 따라서 단어의 자연스러움이 결정될 정도로 중요함..
learning : 기존 hmm 을 어떻게 쓰는지를 이해했는데, learning 은 hmm을 빌드하는 과정 (특정 알고리즘을 사용해서.. em 알고리즘?)
Forward Probabilities

seqeunce classification
- seqeunce 를 만들려면 어떤 hmm을 사용해야하는지..
most likely sequence - a b 중에 HMM에서 어떤게 더 확률이 높을까..
Sequence classification

sentiment classification -> hmm 이용 가능
hmm이 각 클래스별로 존재
-> positive 담당 hmm 에게서 확률 구하기, negative 담당 hmm에게서 확률 구하기
-> 최종적으로 높은 확률의 클래스 선택
Observation likelihood

실질적으로 hmm에서 observation likelyhood 계산하는 방법..
naive하게 생각하면:
- 어떤 상태에 도달했을 때 이 상태의 이전의 상태의 모든 경우를 다 고려해서 계산 -> 현재의 prob 계산
- q_j 의 상태에 도달했을 때 -> 이전 모든 상태의 transition 값과 emission prob를 곱함
- q_j-1 의 상태의 확률 transition prob emission prob 으로 구하기.
- 이전의 모든 상태에서의 값을 모두 더함...
A : transition probability matrix
given observation sequence prob : 현재 상태
-> repeat all possible state sequences..
Compuatational complexity 가 매우 높음
이전 모든 상태의 값을 계속해서 곱하기 때문에 복잡도가 매우 높음
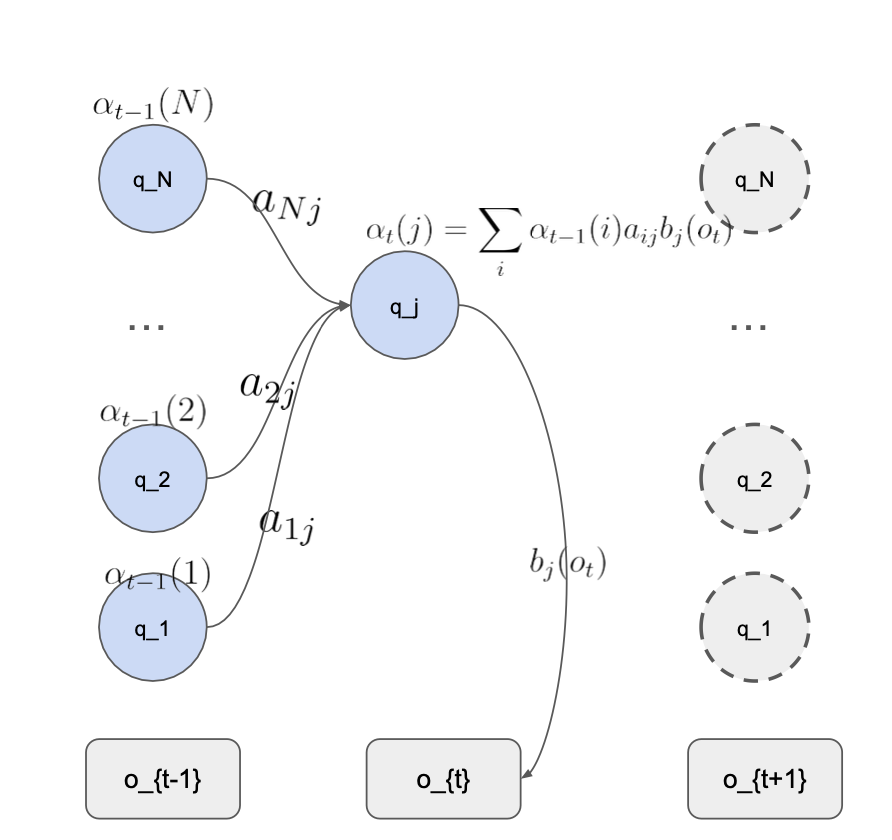
여기서 보면 세로 줄은 N 개의 state -> t 번만큼 반복
= N^T
시퀀스를 한 번 계산할 때 transition(가로줄) 을 T 번 곱함
그래서 O(TN^{T})...
재사용할수있는건 재사용해보자... -> forward algorithm
Forward Algorithm

다이나믹프로그래밍 이용해서 재사용을 하자
single forward trellis
- 격자무늬
- 격자안에서 통과 할 때, 이전에 계산한 값을 재사용하자..
- a1 -> a2 -> a3 라는 시퀀스라면 a3 를 계산할때 a1없이 a2만 고려하자..
- implicitly folds each of these path into a single forward trellis
- 은연중에 계산되고 있던 값을 이용하자...
- a2를 계산할때 a1이 이용됐다는 의미..
q_j 의 확률 값을 계산한다면,
이전의 상태만 고려하면 됨
모든 t (time) 에 대해서 t와 t-1에만 계산해주면 되기 때문에
해당 스텝의 모든 state(N개) 에 대해서 각각 곱해줘야 되기 때문에 ( N * N )
시간복잡도는 O(TN^2) 가 됨.
sample problem

2799년 날씨 예측을 할 수 있을까?
근데 직접적으로 관련된 데이터가 없음, 근데 아이스크림 먹은 데이터가 있음
아이스크림 : observation
날씨 : Hidden state
세개의 시퀀스 존재
Day 1 (3), Day2 (1), Day3 (3)
이걸 기반으로 HMM 을 만듦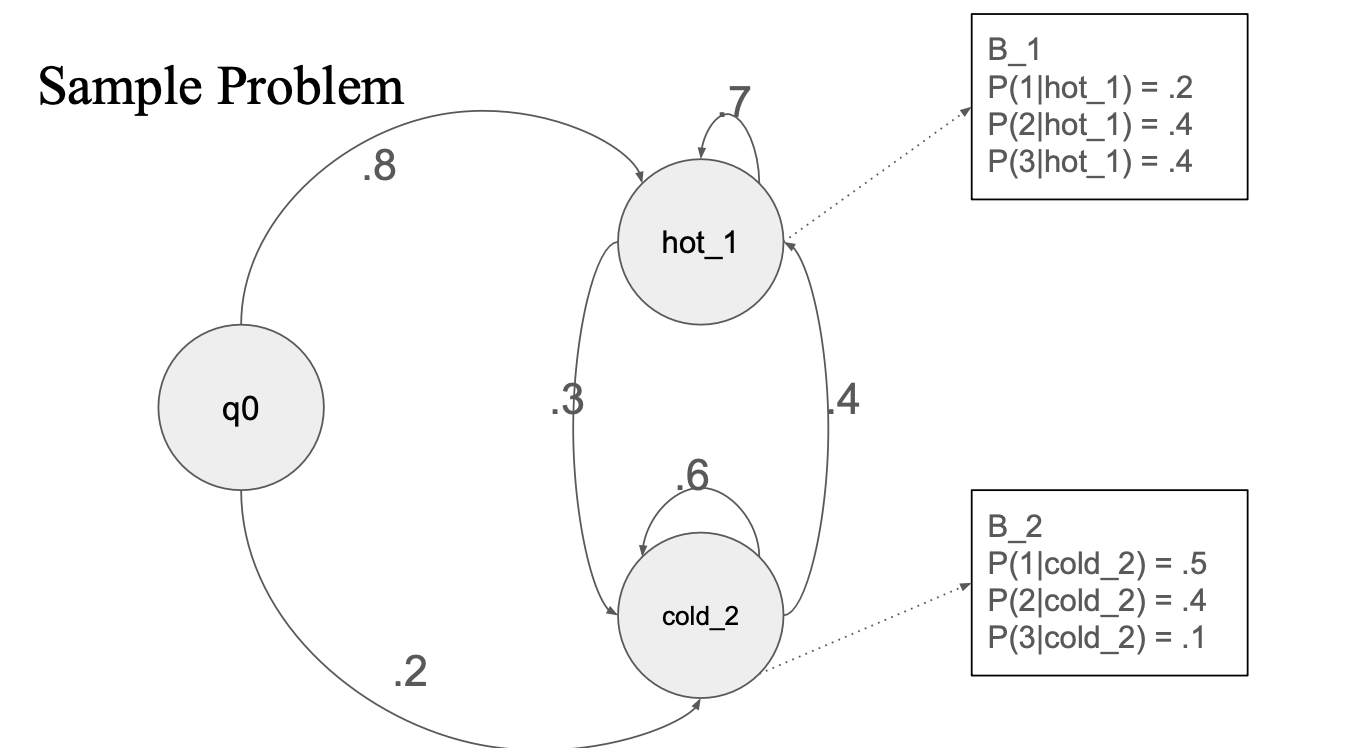
start state : q0
q0 에서 hot, cold 각각의 state 로 가는 transition probability 가 있음
hot 과 cold 라는 hidden state를 예측하고 싶은 것임..
각 state에서 emission probability 가 있음
이 내용을 수식으로 쓰면??
- a(\alpha) : 어떤 state에 대한 확률
- a : transition prob
- b_j(o_t) : emission prob (o_t 가 나올 확률)
Forward algorithm

직전 state (t-1) 에서의 확률만 이용하기.
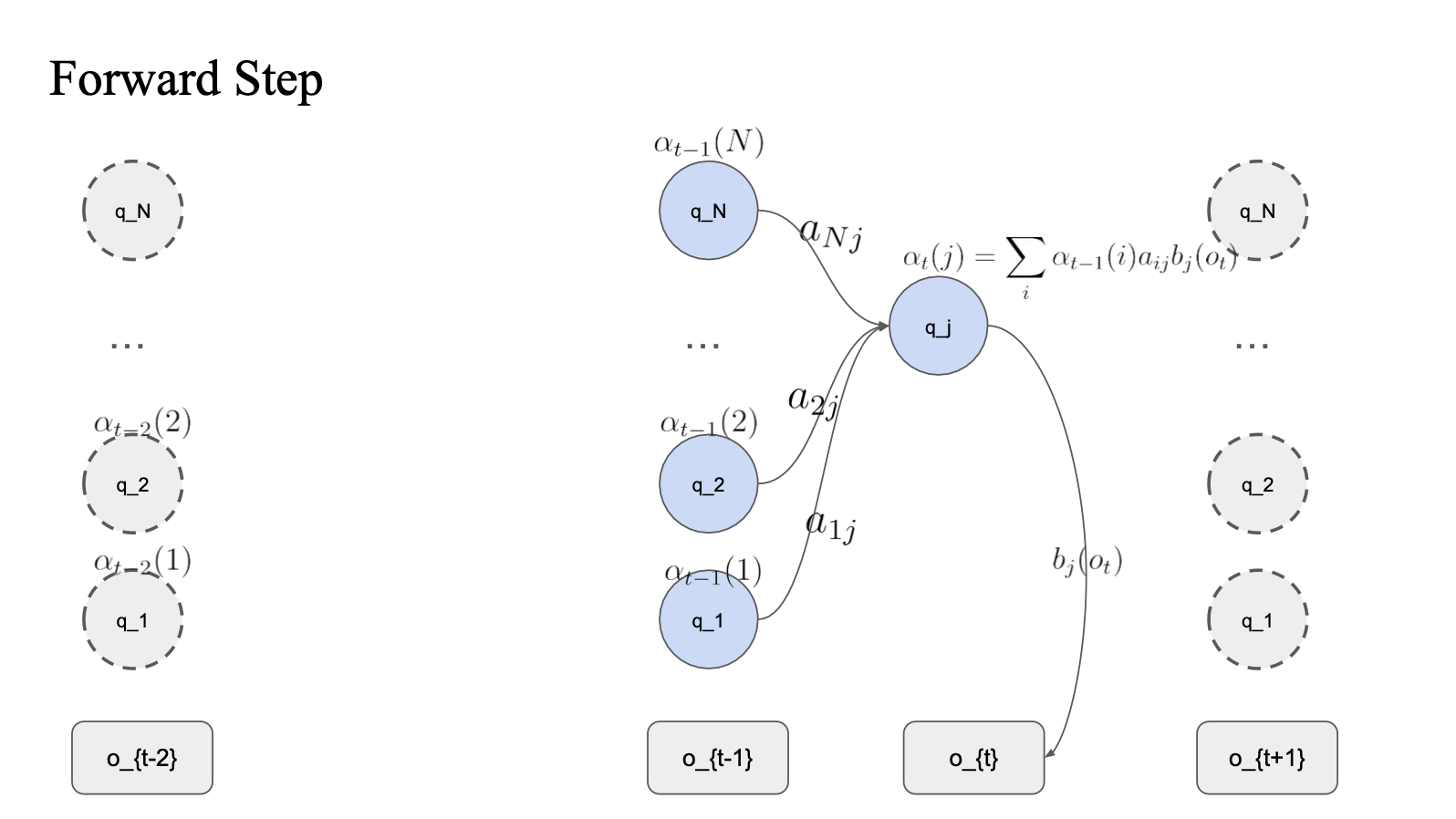
q_j state 의 확률 알파 값을 구할 때
- 이전 상태의 state 확률 * 현재 상태의 state 확률 * Emission prob
Forward step
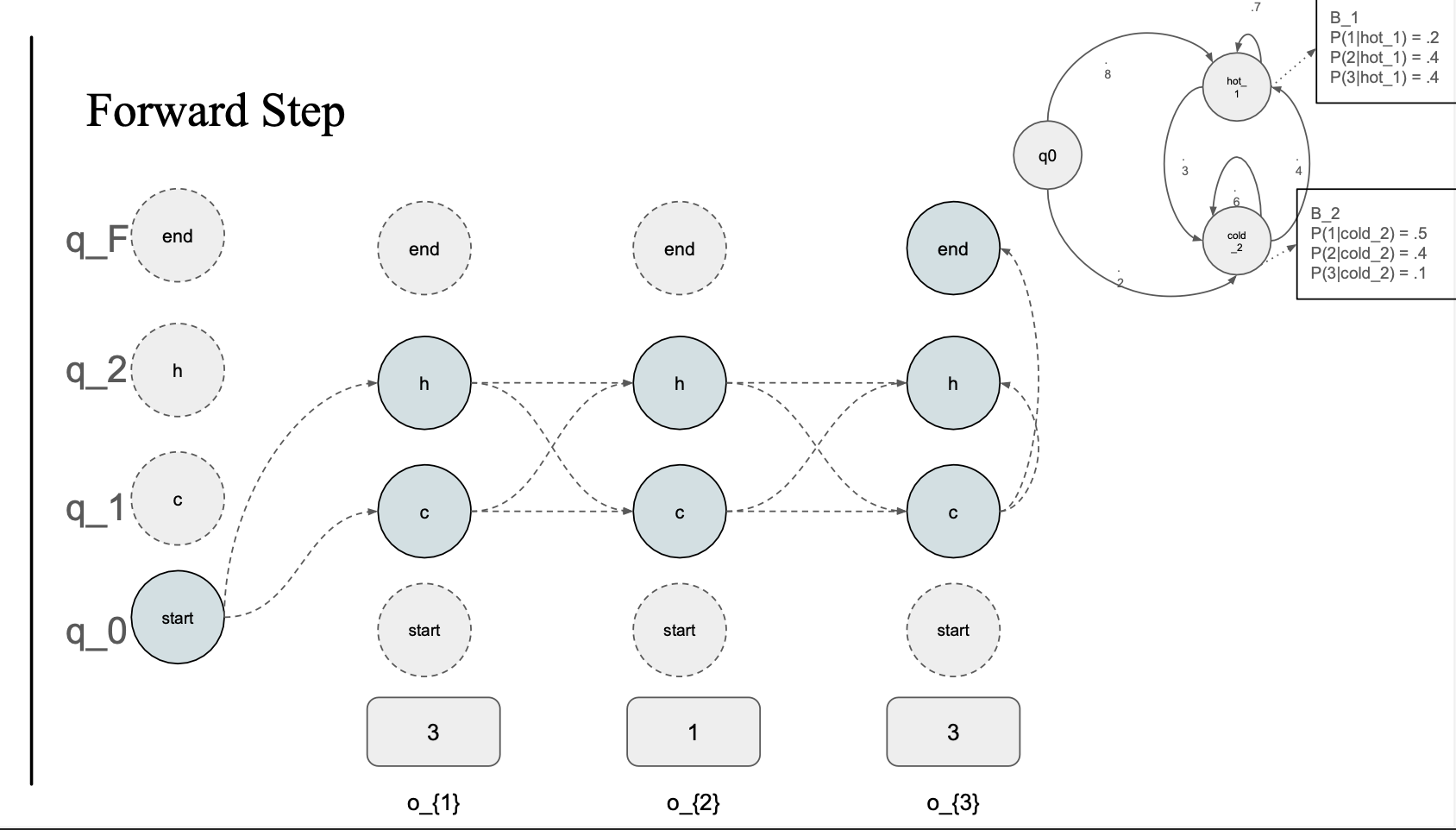
start state 에서 갈 수 있는 모든 state 에 대해서 \alpha 를 계산해줌
o_{1} state들의 확률
- q_0 -> h :
- 0.8 * 0.4(emission(3)) = 0.32
- q_0 -> c :
- 0.2 * 0.1(emission(3)) = 0.02
그리고 이제 o{2} state를 계산할 때
o{1} state의 확률 값을 가지고 계산 -> dp 를 이용한 재사용이다..
이 방식으로 state에 도달할 확률을 계속해서 구해줌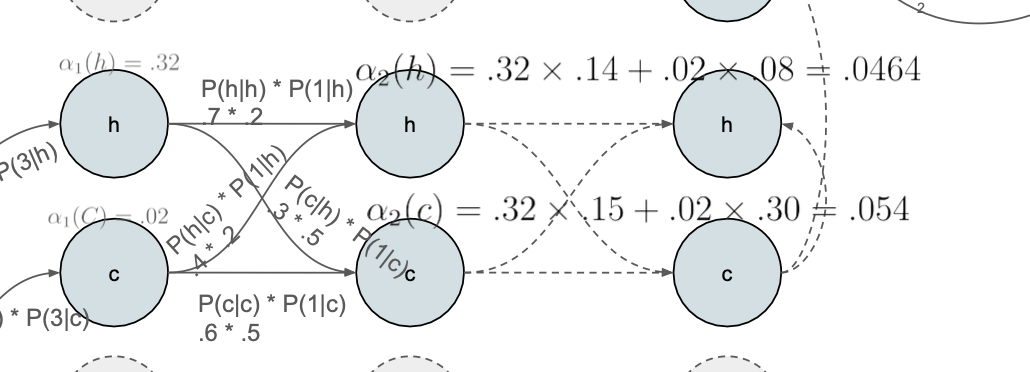
이때 h -> c, c -> c 하나의 state에 도달하는 경우가 두개 이상인데, 이 값들을 더해줌
0.32 * 0.14 + 0.2 * 0.8 = 0.464
- 이 과정이 이 수식이다.
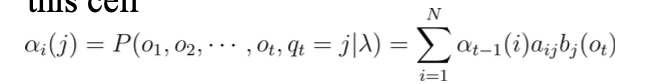
최종적으로는
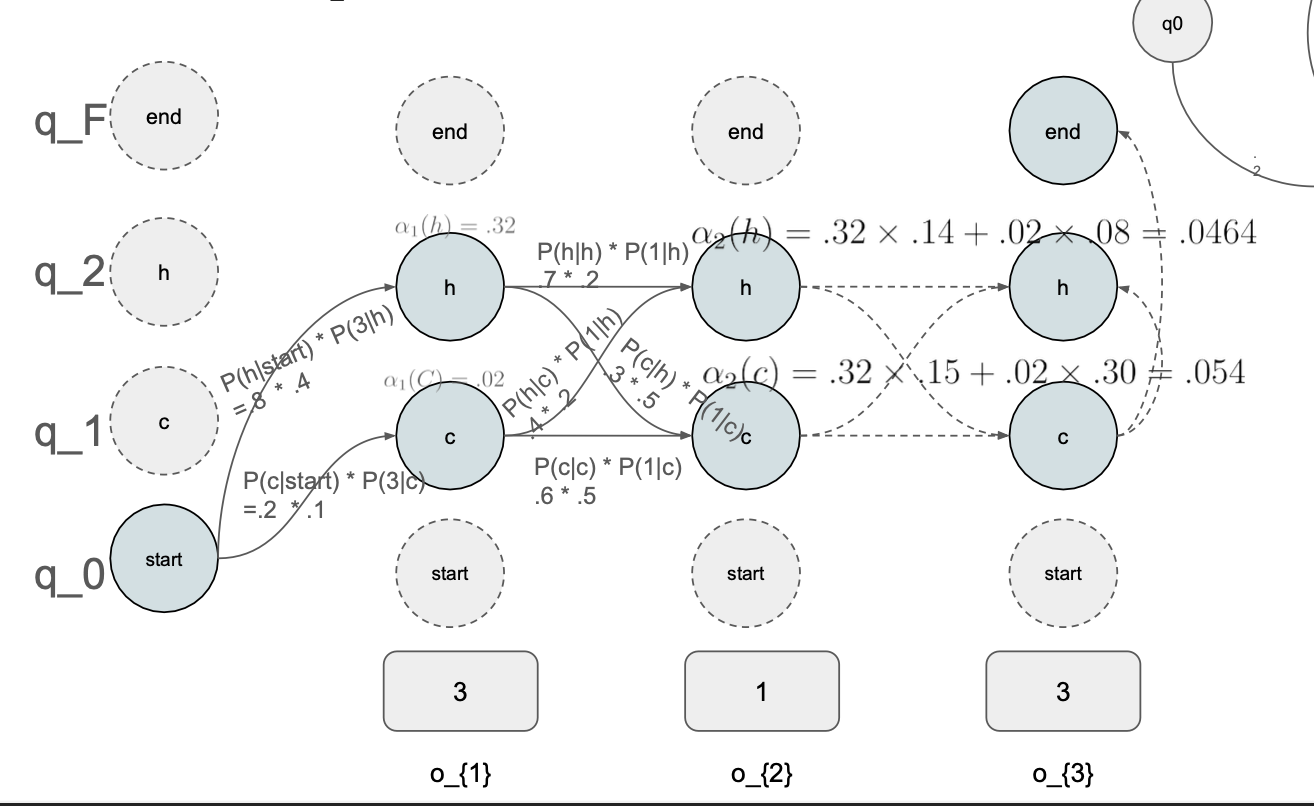
final state에서는 모든 state에서 오는 값을 더해줌..
3 1 3 이라는 observation 을 예측했다..
Viterbi algorithm


더하는게 아니고 max로 만들어주는 확률을 골라서 해당 state의 확률로 저장해줌
bt(backpointer) : 백트레킹할때 어떤 state에서 온 값인지 알기 위해 사용하는 notation

viterbi(max값 선택) -> backpointer
forward 와 viterbi 차이점
Viterbi is basically the forward algorithm + backpointers, and substituting a max function for the summation operator
forward는 다 더해줬는데, 비터비는 max값을 선택하고 backpointer를 저장한다.
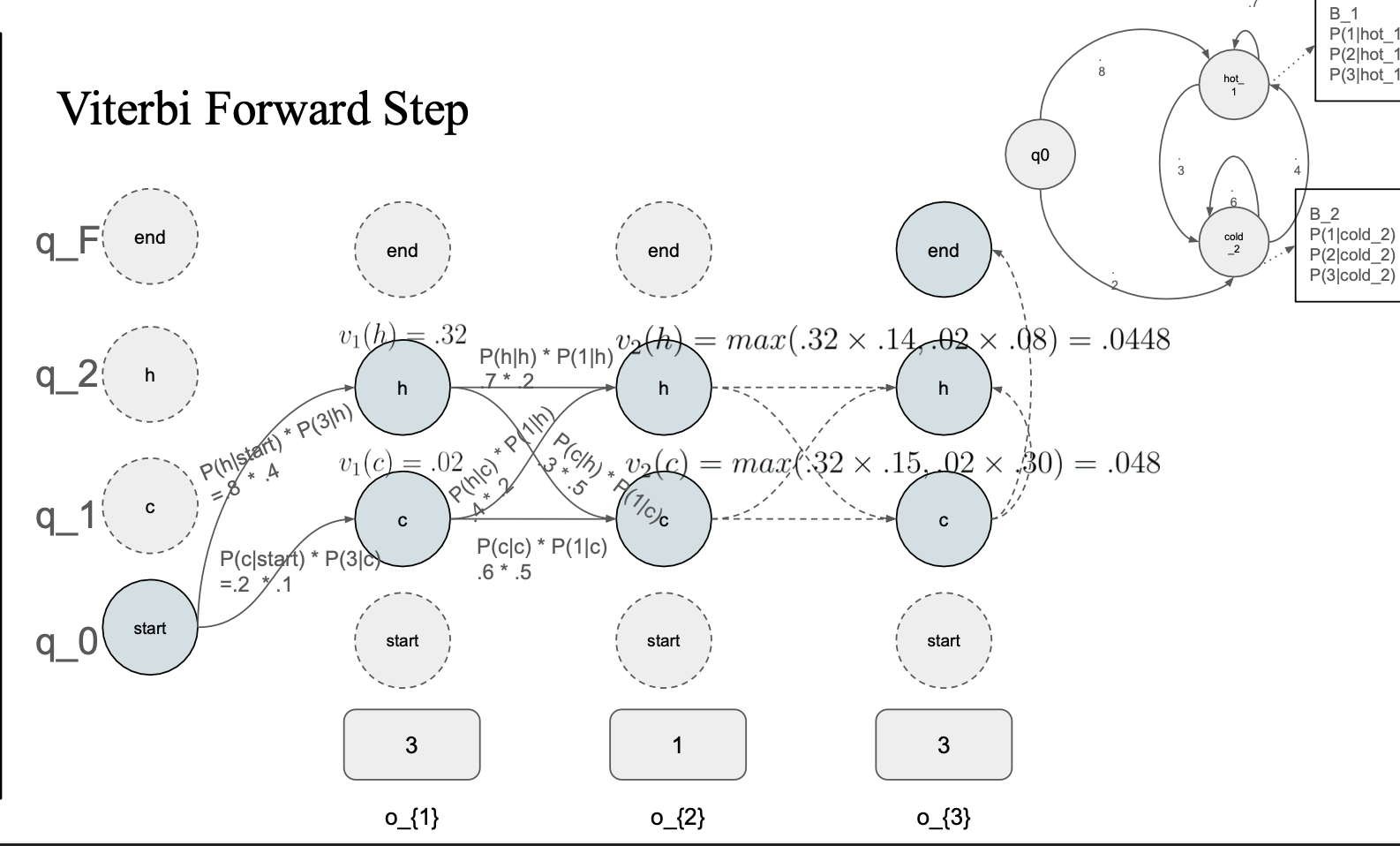
max값을 계속 저장
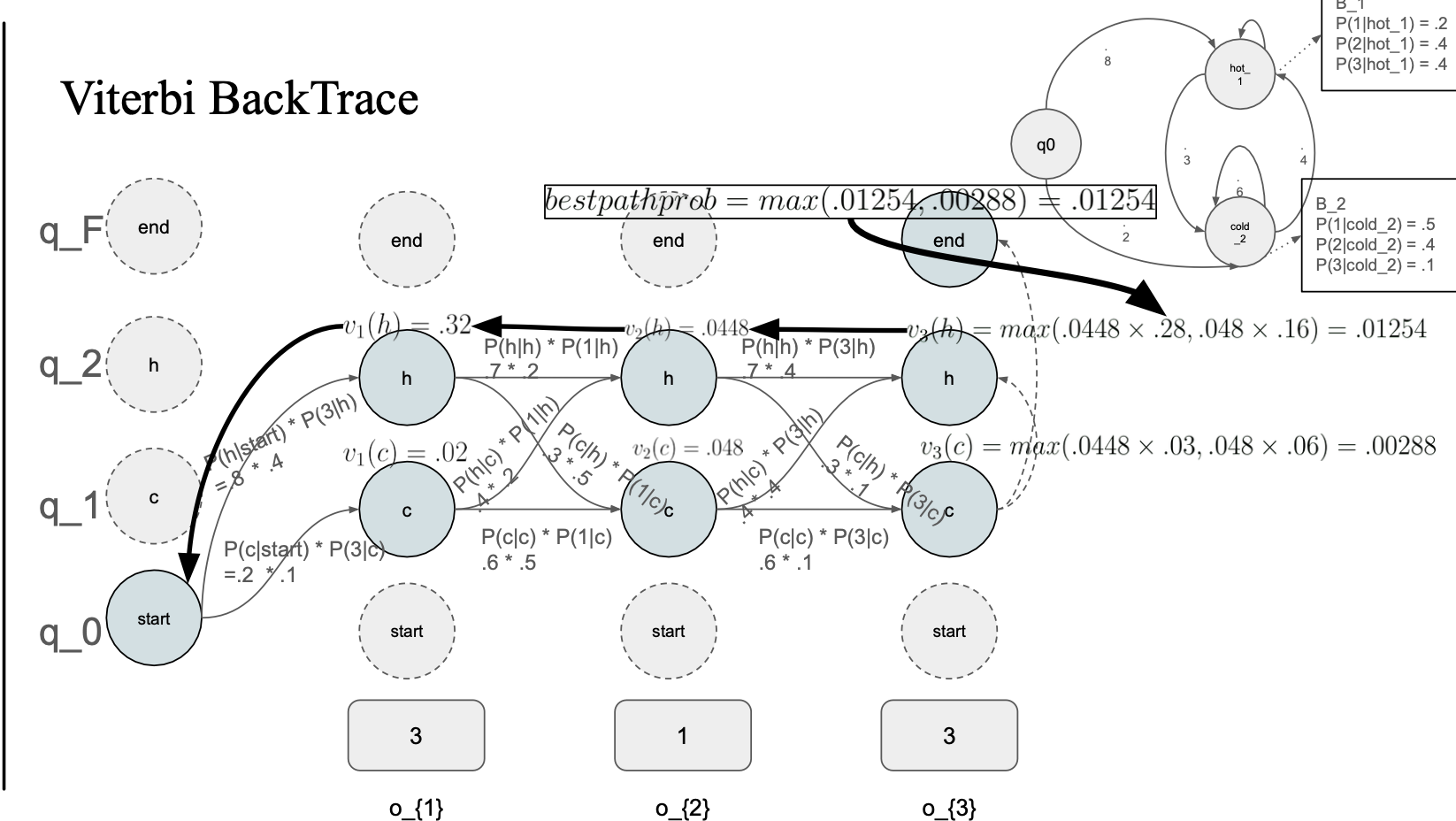
0.01254 는 어디서 왔지?
- 이전 state hot 에서 왔고
- 그 이전 state는 hot
- 그 이전 state 도 hot
그러면 hot -> hot -> hot 으로 날씨 예측을 할 수 있다...
- 이것이 hmm 의 목적
