Camera Distortion

Lily·2024년 1월 8일

Distortion

TIL

목록 보기

21/21

완벽한 Pinhole 카메라는 빛이 하나의 점을 통과하지만, 렌즈는 크기를 가지는 물체이기 때문에 빛이 다르게 굴절된다.
렌즈의 표면 상 매끄럽지 않는 부분에서 굴절하는 동안 오차가 발생하기도 한다.
빛의 굴절은 이미지 센서에 보이는 이미지를 왜곡한다.
ex) 사진 가장자리에서의 건물 벽이 곡선으로 보인다, etc.

$\\$
$\\$

이미지 왜곡 원인

렌즈의 형상에 따라 왜곡 발생
렌즈와 이미지 센서와의 관계로 인해 왜곡 발생

$\\$
$\\$

방사 왜곡

일반적으로 볼록렌즈를 많이 사용한다. 오목렌즈, 직각렌즈에 따라서도 왜곡이 다른 양상으로 발생할 수 있다.
왜곡은 렌즈 형상이 곡률을 가지는 구면 형태이기 때문에 발생한다.
따라서 이미지 중심부 (정확히는 주점, Principal Point) 에서 멀어질수록 표현의 비율이 달라지기 때문에 발생한다.

Barrel Distortion: 중심부가 외각부보다 큰 형태로 발생
Pincushion Distortion: 중심부가 외각부보다 작은 형태로 발생
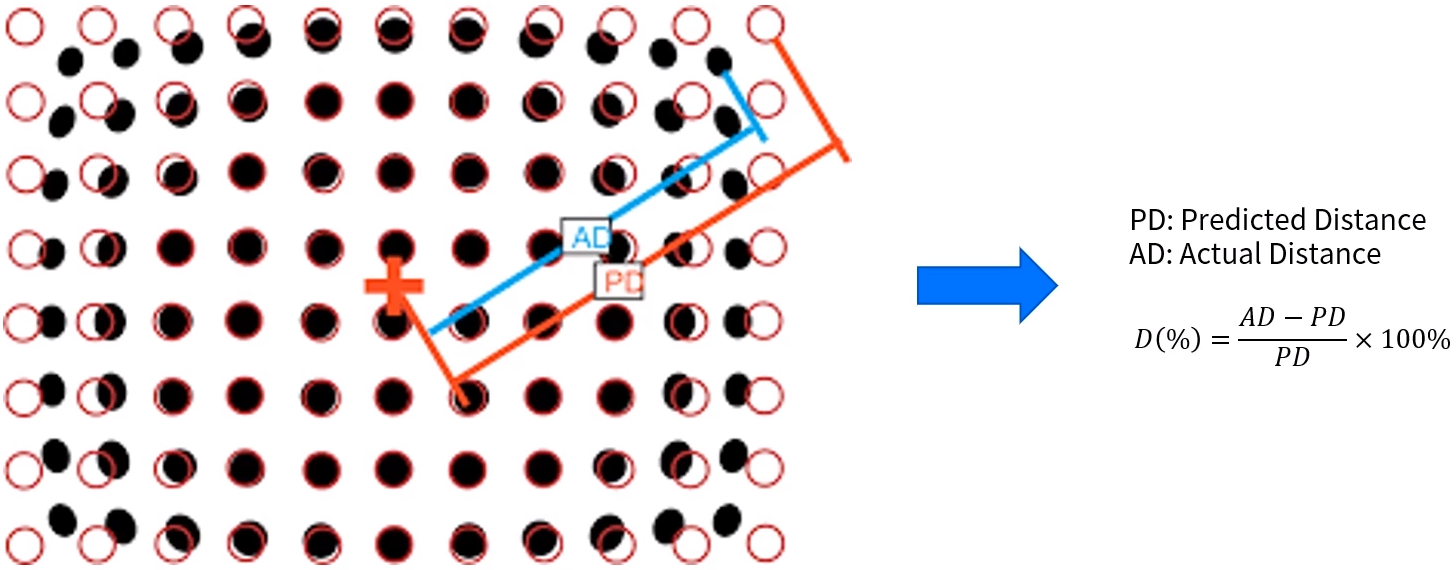
방사 왜곡은 이미지의 중심으로부터 멀어질수록 왜곡의 정도가 심해진다. (앞선 이미지의 D(%)를 계산하여 확인 가능)

$\\$
$\\$

접선 왜곡

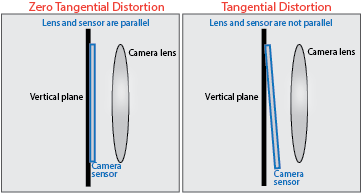
Tangential Distortion이라고도 한다.
접선 왜곡은 카메라 제조 공정에서 발생하는 왜곡으로, 렌즈와 이미지 센서와의 수평이 맞지 않는 경우 발생한다.

$\\$
$\\$

그 외 왜곡

원근 왜곡(Perspective Distortion)이 있다.
방사 왜곡과 접선 왜곡이 광학의 원리와 카메라에서 발생하는 왜곡이라면, 원근 왜곡은 3차원 공간이 2차원 공간으로 투영되면서 발생하는 왜곡이다.
이미지는 공간의 깊이 정보가 하나의 평면으로 투영되는 데이터이기 때문에, 원근감이 손실이 되면 이를 회복할 방법이 없고, 이미지를 촬영하는 환경에 따라 다양한 왜곡이 만들어질 수도, 만들 수도 있다.

$\\$
$\\$

원근감을 복구하는 방법 (feat. SLAM)

다수의 카메라를 사용하는 방법
- 2개 이상의 카메라로 동일한 시점에 촬영한 각 1장의 이미지 만으로 3차원 위치 정보를 추정할 수 있다.
- 각 카메라의 Extrinsic Parameter를 알아야 정확한 정보를 추정할 수 있다.
2장 이상의 이미지를 사용하는 방법
- 같은 카메라로, 카메라가 움직이는 환경에서 연속된 이미지 정보를 활용하여 3차원 위치 정보를 추정할 수 있다.
- 카메라의 움직임 정보를 정밀하게 측정 & 추정해야 정확한 정부를 얻을 수 있다.

$\\$
$\\$

왜곡 보정 방법

카메라 좌표계를 기준으로, 3차원 공간상에 존재하는 객체를 투영하는 모델을 계산했을 때, 기본 연산은 다음과 같다.

$s\begin{bmatrix}x \\y \\ 1 \end{bmatrix} = \begin{bmatrix}f_x & skew\_cf_x & c_x \\0 & f_y & c_y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix}r_{11} & r_{12} & r_{13} & t_1 \\r_{21} & r_{22} & r_{23} & t_2 \\ r_{31} & r_{32} & r_{33} & t_3 \end{bmatrix} \begin{bmatrix}X_C \\Y_C \\ Z_C \\ 1 \end{bmatrix}$

Extrinsic Calibration은 왜곡 모델에 불필요하니 Extrinsic 영향이 없다고 가정하면 행렬은 Identity Matrix가 된다.
Normalized Image Plane에 투영된다고 하면 Intrinsic Matrix를 연산할 필요가 없다.
따라서, $s\begin{bmatrix}x \\y \\ 1 \end{bmatrix} = \begin{bmatrix}X_C \\Y_C \\ Z_C \\ 1 \end{bmatrix}$ 이 된다. 이를 정리하면,
$s\begin{bmatrix}u_{n_u} \\v_{n_u} \end{bmatrix} = \begin{bmatrix}X_C/Z_C \\Y_C/Z_C \end{bmatrix}$ , 여기서 $u$ 는 undistort의 약자이다.

왜곡이 없는 이미지 => 왜곡이 있는 이미지 변환

Undistort에 Distortion 모델을 적용하면 다음과 같다:
(첫번째 괄호식: Radial Distortion, 두번째 행렬식: Tangential Distortion)

$\begin{bmatrix}u_{n_d} \\v_{n_d} \end{bmatrix} = (1+k_1 r_u^2+k_2 r_u^4+k_3 r_u^6)\begin{bmatrix}u_{n_u} \\v_{n_u} \end{bmatrix}+\begin{bmatrix}2p_1 u_{n_u}v_{n_u} + p_2(r_u^2+2u_{n_u}^2)\\p_1(r_u^2+2v_{n_u}^2)+2p_2 u_{n_u}v_{n_u} \end{bmatrix}$
여기서, $r_u^2=u_{n_u}^2+v_{n_u}^2$ 이 된다.
Normalized Image Plane을 Image Plane으로 변환하면,

$\begin{bmatrix}x_{p_d} \\y_{p_d} \\ 1 \end{bmatrix} = \begin{bmatrix}f_x & skew\_cf_x & c_x \\0 & f_y & c_y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix}u_{n_d} \\v_{n_d} \\ 1 \end{bmatrix}$

왜곡이 있는 이미지 => 왜곡이 없는 이미지 변환

앞서 계산한 두 수식을 거꾸로 계산하면 가능하다.
Image Plane에 투영한 Normalized Image Plane의 계산 식을 역으로 계산하면 $x_{p_d} \rightarrow u_{n_d}, y_{p_d} \rightarrow v_{n_d}$ 값을 얻게 된다.
이 $u_{n_d}, v_{n_d}$ 를 distortion 수식에 대입하고, 이미지 캘리브레이션으로 나온 $k_*, r_*, p_*$ 를 대입해서 $u_{n_u}, v_{n_u}$ 를 구하면 된다.
사실상 OpenCV::undistort 혹은 initUndistortRectifyMap + remap 함수를 사용하면 된다.