Camera Intrinsic Calibration

카메라의 Intrinsic Parameter를 정리하면 다음과 같다.

$Intrinsic = \begin{bmatrix}f_x & skew\_cf_x & c_x \\0 & f_y & c_y \\ 0 & 0 & 1 \end{bmatrix}$

매트릭스의 각각의 요소에 대해 알아보도록 하겠다.

$\\$
$\\$

Focal length $f_x, f_y$

• Focal length는 렌즈와 이미지 센서의 거리이다.

• Computer Vision 에서 초점거리는 Pixel 단위로 표현한다. (디지털 카메라에서 사용하는 초점거리와 단위가 다르다.)

• 카메라(또는 광학)에서는 초점거리를 실제 물리 단위인 mm로 표현한다.

  • 이미지 센서(CCD or CMOS)와 렌즈 중심과의 거리

• 하지만 Computer Vision에서는 이미지 센서의 Cell 크기에 대한 상대적인 Pixel 단위로 표현한다.

  • 만약 이미지 센서 Cell 크기가 0.1mm이고 초점거리 f=500(pixel) 이라면
  • 이미지 센서와 렌즈 중심과의 거리는 Cell 크기의 500(pixel)배 -> 50mm를 의미한다.

• 이는 이미지 해상도에 따라 초점거리(pixel)가 달라지는 이유이기도 하다. (이게 왜 중요하고, 어디에 연관되어 있을까?)

• Case 1)

  • 100x100 Cell Size (0.1mm)
  • 100x100 Image 해상도 (Resolution)
    -> 1x1 Cell이 하나의 Pixel을 표현한다.
    -> 따라서 0.1mm * Focal Length(Pixel) = Focal Length(mm)

• Case 2)

  • 100x100 Cell Size (0.1mm)
  • 50x50 Image 해상도
    -> 2x2 Cell이 하나의 Pixel을 표현한다.
    -> 따라서 0.2mm * Focal Length(Pixel) = Focal Length(mm)
    -> 물리적인 초점거리는 동일하기 때문에 Pixel 단위의 초점거리는 절반으로 줄어든다.

$\\$
$\\$

Question

• $f_x, f_y$ 각각이 존재하는 이유?

$\\$
$\\$

Principal Point, $c_x, c_y$

• Pinhole 카메라에서 렌즈가 있고, 그 뒤에 이미지 센서가 있다면, 렌즈 중심에서 빛이 통과했을 때, 이미지 센서에 직교하는 위치를 주점 $c_x, c_y$로 정의한다.

• 이상적인 상황에서의 주점은, 이미지 (센서?)의 width, height가 주어졌을 때, 다음과 같다.

  • $c_x$ = $\displaystyle\frac{width}{2}$
  • $c_y$ = $\displaystyle\frac{height}{2}$

• 주점(Principal Point)과 이미지 중심점(Center Point)와 헷갈리는 경우가 많지만, 이는 다른 의미이다.

• 주점(=렌즈 중심점)이 이미지 중심점과 일치하는 경우가 이상적이지만, 카메라 제조 공정에서 발생하는 다양한 이슈로 일치하지 않는 경우가 있다.

$\\$
$\\$

$skew\_cf_x$

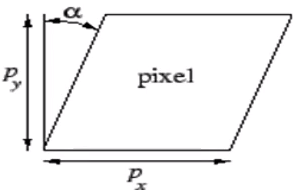
• $skew\_cf_x$는 이미지의 비대칭 계수(skew coefficient)를 의미한다.

• 비대칭 계수는 이미지 센서의 Cell Array의 y축이 기울어진 정도를 의미한다.

• 예전 카메라의 경우는 이런 왜곡 정도가 있었지만, 최근 카메라엔 거의 발생하지 않는다. 0으로 치부해도 상관 없음

$\\$
$\\$

카메라 좌표계

• 카메라 투영과정을 이해하게 된다면, Intrinsic Calibration이 어떻게 적용되는지 확인할 수 있다.

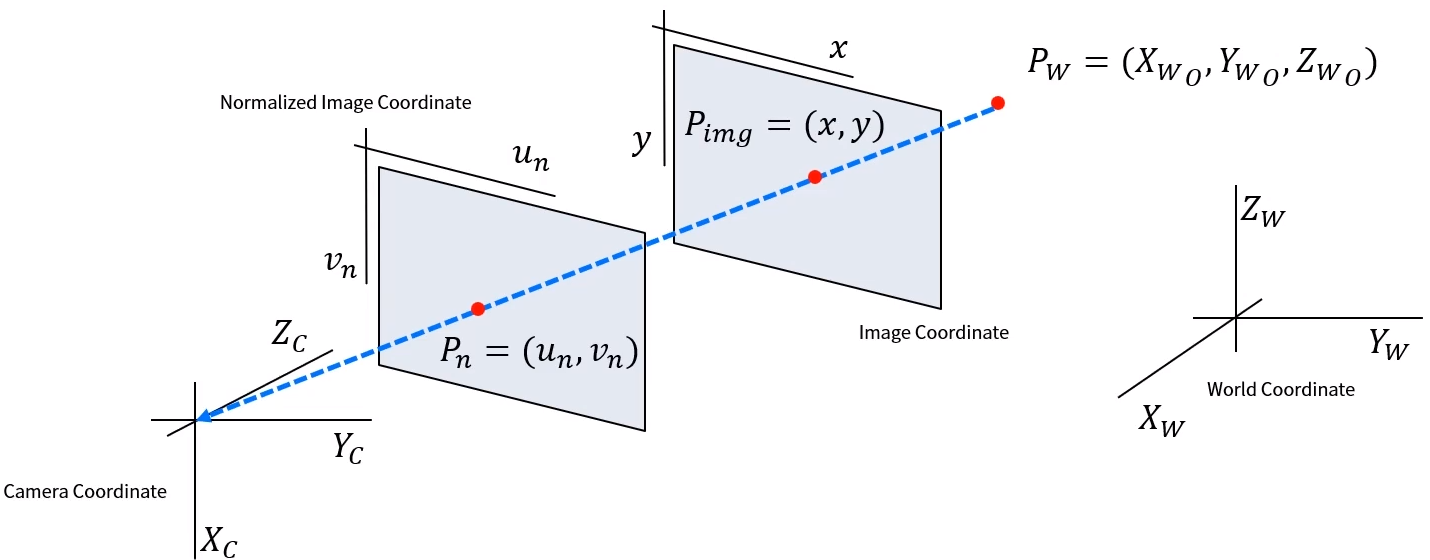
• World Coordinate: $X_W, Y_W, Z_W$

  • 원점을 필요로 한다: 기준을 정하기 나름인데, 카메라 좌표계를 원점으로 정하기도 한다.

• Camera Coordinate: $X_C, Y_C, Z_C$

  • 카메라 좌표계의 원점은, 이미지 센서의 중심점(?)
  • $Z_C$: 카메라 렌즈가 바라보는 방향
  • $X_C$: 카메라 아래쪽 방향
  • $Y_C$: 카메라 오른쪽 방향
  • 카메라 좌표계와 월드 좌표계의 기준 방향이 다르기 때문에, 변환할 때 조심해야 하는데, $Z_C$ -> $X_W$, $X_C$ -> $Z_W$로 변환하는 것으로 생각하면 된다.

• Image Coordinate: $u, v$

  • 실제 바라보고 있는 사진, 이미지에 해당하는 좌표계
  • 왼쪽 상단을 원점, 오른쪽 방향을 x(=$u$), 아래 방향을 y(=$v$)로 정의

• Normalized Image Coordinate: $u_n, v_n$

  • 실제로 존재하지 않는 좌표계
  • 기하학적 해석을 잘 하기 위해 정의한 가상의 좌표계
  • 렌즈로부터 이미지 평면까지의 거리를 초점거리라고 정의하였다.
  • 같은 물체를 동일한 위치에서 서로 다른 카메라로 촬영할 경우, 이미지에서 다르게 표현된다.
  • 즉, 카메라마다 초점거리가 다르기 때문에 이미지 좌표계에서 다른 위치에 존재한다.
  • 따라서 초점거리의 영향을 제거하기 위해, 초점거리를 1로 정규화 한 가상의 이미지 좌표계를 사용한다.

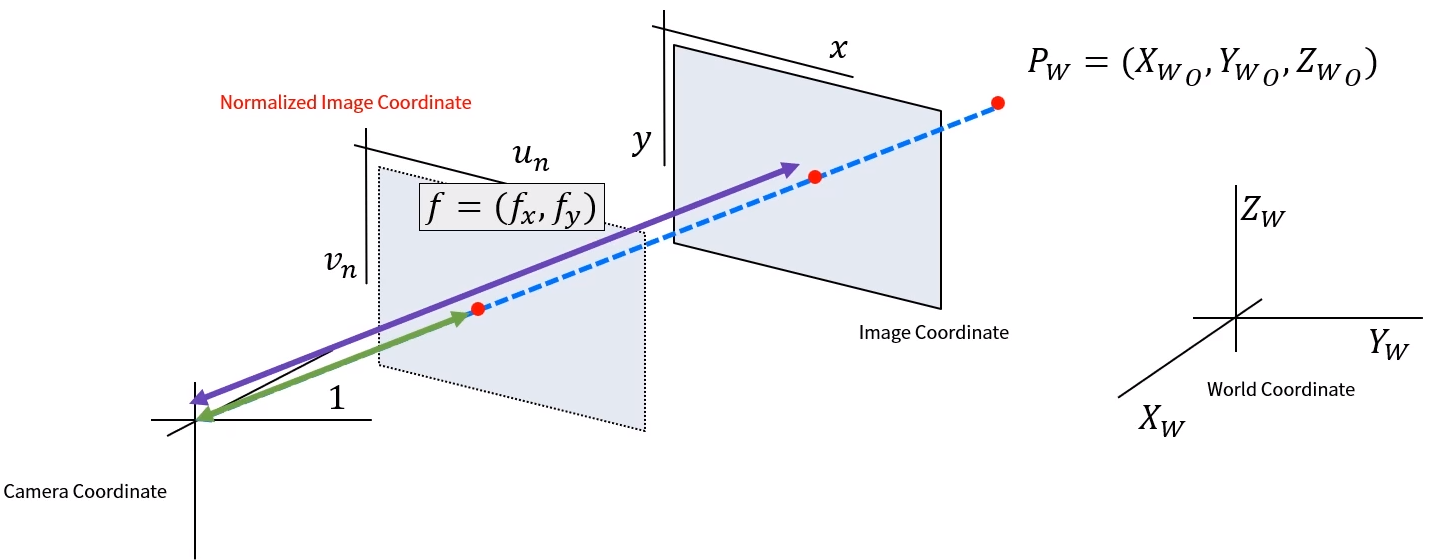
• 정규 이미지 좌표계와 이미지 좌표계의 차이

  • 이미지 좌표계 -> 카메라 원점으로부터 초점거리 만큼 떨어져 있는 이미지 평면 (보라색 쌍화살표)
  • 정규 이미지 좌표계 -> 카메라 원점으로부터 1만큼 떨어져 있는 가상의 이미지 평면 (녹색 쌍화살표)

• 이미지의 정규화: 정규 이미지 좌표계와 이미지 좌표계의 변환 관계

  • 카메라의 Intrinsic Calibration 정보를 알면($f_x, f_y, c_x, c_y$), 이미지 좌표계 -> 정규 이미지 좌표계로 변환이 가능하다. (Vise versa)

  • $\begin{bmatrix}u \\v \\ 1 \end{bmatrix} = \begin{bmatrix}f_x & 0 & c_x \\0 & f_y & c_y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix}u_n \\v_n \\ 1 \end{bmatrix}$

  • 행렬 곱셈을 수행하여 풀어보면,

  • $u=f_x u_n + c_x \Longleftrightarrow u_n=\displaystyle\frac{(u-c_x)}{f_x}$,

  • $v=f_y v_n + c_y \Longleftrightarrow v_n=\displaystyle\frac{(v-c_y)}{f_y}$,

• $u_n, v_n$ 정보를 알게 되면, 다른 카메라의 Intrinsic Callibration 파라메터들을 활용해 다시 다른 카메라의 이미지 좌표 $u, v$를 생성해 낼 수 있으나, 이미지가 이빨이 빠지거나 군데군데 비어있을 수 있다. 하지만 다양한 응용 방법을 고안할 수 있다.

$\\$
$\\$

References

• 자율주행 데브코스 사지원 강사님