OpenCV 엣지 검출 - (2)

허프 변환 직선 검출

• 2차원 영상 좌표에서의 직선의 방정식을 파라미터 공간으로 변환하여 직선을 찾는 알고리즘

  $y=ax+b \Longleftrightarrow b=-xa+y$

• 축적 배열(accumulation array)

  • 직선 성분과 관련된 원소 값을 1씩 증가시키는 배열
  • $y=ax+b$에서 $(x_{i},y_{i})$ 값을 각각의 기울기와 절편으로 표시해 a축, b축에서 일치하는 부분들을 카운팅하면, 가장 많이 증가된 부분이 바로 이미지에서 (a,b) 좌표임을 알 수 있음
  • 축적시키는 행위를 voting으로도 표현해서 voting 알고리즘이라고도 부름

• 직선의 방정식 $y=ax+b$를 사용할 때의 문제점

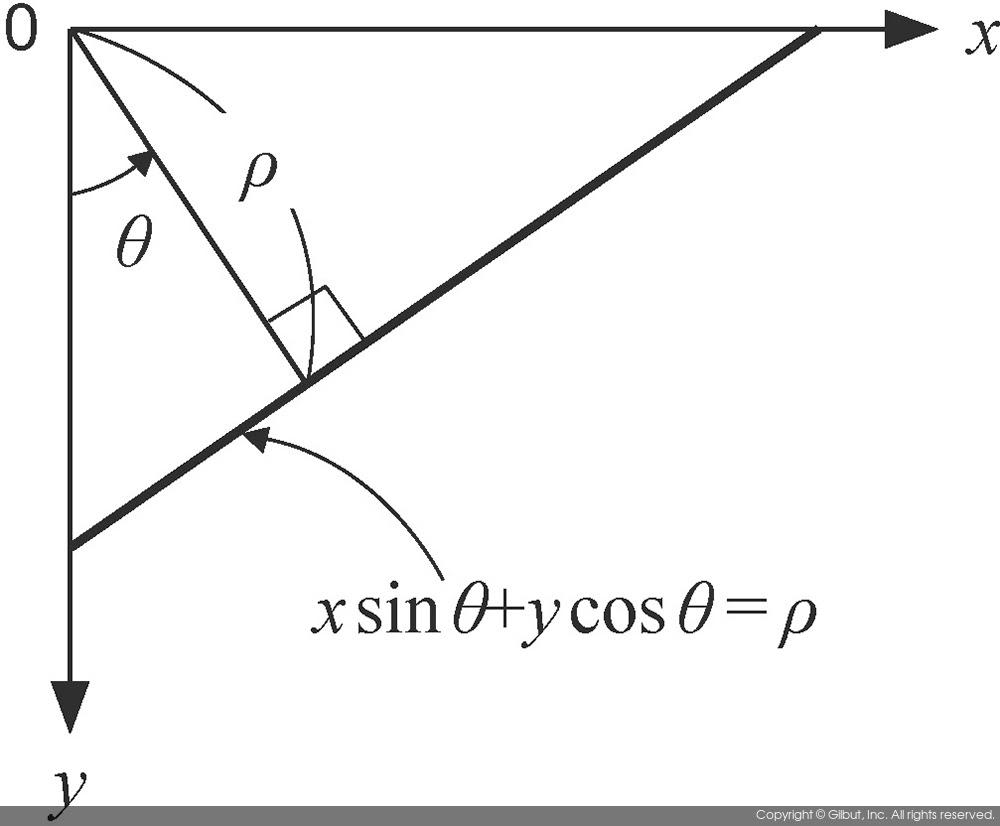
  • y축과 평행한 수직선을 표현하지 못함 -> 극좌표계 직선의 방정식을 사용

    

  $xcos\theta+ysin\theta=\rho$

• 허프 변환의 파라메터들은 $(\rho, \theta)$ 로, 앞선 $x,y$ 를 $a,b$ 로 변환시켰을 때 처럼 $\theta$ 축, $\rho$ 축으로 변환해 곡선의 형태를 띠는 그래프를 만들게 된다. 이 때 겹쳐지는 한 점이 바로 $(\rho_{0}, \theta_{0})$일 때, 극대값을 갖는다.

허프 변환 직선 검출 함수

void HoughLines(InputArray image, OutputArray lines,
				double rho, double theta, int threshold, 
                double srn=0, double stn=0, 
                double min_theta=0, double max_theta=CV_PI);

• image: 그레이스케일 엣지 영상
• lines: 직선의 파라미터(rho, theta)를 저장할 출력 벡터. vector<Vec2f>
• rho:
  • 축적 배열에서 rho 값의 간격. 픽셀 단위. ex) 1.0 : 1픽셀 간격
  • 이 값이 커지면 속도는 증가하고 정확도는 내려감
• theta: 축적 배열에서 theta 값의 간격. 라디안 단위. ex) CV_PI/180 : 1도 간격
• threshold: 축적 배열에서 직선으로 판단할 임계값
• srn: 멀티스케일 허프 변환에서 rho 해상도와 rho/srn 해상도를 각각 이용하여 멀티스케일 허프 변환을 수행. srn과 stn이 모두 0이면 일반 허프 변환을 수행
• stn: 멀티스케일 허프 변환에서 theta 해상도를 나누는 값
• min_theta: 검출할 직선의 최소 theta 값
• max_theta: 검출할 직선의 최대 theta 값

확률적 허프 변환 직선 검출 함수

void HoughLinesP(InputArray image, OutputArray lines,
				double rho, double theta, int threshold,
                double minLineLength=0, double maxLineGap=0);

• image: 그레이스케일 엣지 영상
• lines: 선분의 시작, 끝 좌표 (x1,y1,x2,y2), 저장할 출력 벡터 vector<Vec4i>
• rho:
  • 축적 배열에서 rho 값의 간격. 픽셀 단위. ex) 1.0 : 1픽셀 간격
  • 이 값이 커지면 속도는 증가하고 정확도는 내려감
• theta: 축적 배열에서 theta 값의 간격. 라디안 단위. ex) CV_PI/180 : 1도 간격
• threshold: 축적 배열에서 직선으로 판단할 임계값
• minLineLength: 검출할 선분의 최소 길이
• maxLineGap: 직선으로 간주할 최대 엣지 점 간격, 중간에 끊긴 점 픽셀을 얼마까지 용인할 것인지

$\\$
$\\$

허프 변환 원 검출

• 원의 방정식 : $(x-a)^{2} + (y-b)^2=c^{2}$ -> 3차원 축적 평면?
  

• 속도 향상을 위해 Hough gradient method 사용

  • 입력 영상과 동일한 2차원 평면 공간에서 축적 영상을 생성
  • 엣지 픽셀에서 그래디언트 계산
  • 그래디언트 방향에 따라 직선을 그리면서 값을 누적
  • 원의 중심을 먼저 찾고, 적절한 반지름을 검출
  • 단점: 동심원이 있을 시 가장 작은 크기의 원만을 찾을 수 있음

허프 변환 원 검출 함수

void HoughCircles(InputArray image, OutputArray circles,
				int method, double dp, 
                double minDist=0, double param1=100, double param2=100,
                int minRadius=0, int maxRadius=0);

• image: 그레이스케일 일반 영상
• circles: 원의 파라미터(cx, cy, r)를 저장할 출력 벡터. Mat (CV_32FC3) 또는 vector<Vec3f>
• method: HOUGH_GRADIENT 또는 HOUGH_GRADIENT_ALT 지정
  • HOUGH_GRADIENT_ALT: OpenCV 4.3 부터 지원하며, HOUGH_GRADIENT 보다 더 좋은 성능을 나타냄
• dp: 입력 영상과 축적 배열의 크기 비율
  • 1: 동일 크기
  • 2: 입력 영상의 가로와 세로 크기의 1/2 크기의 축적 배열 사용
  • 축적 배열이 크면 정확도 향상, 연산속도 증가
  • 축적 배열이 작으면 정확도 떨어지지만 연산속도 감소
  • 축적 배열을 작게 하면, 살짝 Blurring 효과(민감하게 반응하지 않도록)를 주는 것이기도 함
• minDist: 검출된 원 중심점들의 최소 거리, 동일한 원을 여러번 검출 하지 않도록 값을 잘 조정할 수 있음
• param1: 케니 엣지 검출기의 큰 임계값($T_{High}?$), $T_{Low}$는 절반 값으로 자동 설정됨
  • HOUGH_GRADIENT_ALT는 Sharr 필터를 사용하므로 Sobel 필터를 사용하는 HOUGH_GRADIENT방법(100~200)보다 큰 임계값을 지정(300~400)
• param2: 축적 배열에서 이 값보다 큰 위치의 중심점 좌표를 선택하도록 설정
  • HOUGH_GRADIENT 방법에서는 축적 배열 임계값
  • HOUGH_GRADIENT_ALT 방법에서는 원의 perfectness 값 (1에 가까울수록 완벽한 원, 0.8~1.0 사이 값 지정)
• minRadius: 검출할 원의 최소 반지름
• maxRadius: 검출할 원의 최대 반지름

$\\$
$\\$

코너 검출

• 코너의 특징:
  • 두 엣지의 교차점. 서로 다른 방향의 엣지가 공존하는 점.
  • 평탄한(flat) 영역과 엣지(edge) 영역은 고유한 위치를 찾기 어려움
  • 코너는 변별력이 높은 편이며, 영상의 이동 및 회전 변환에 강인함

해리스 코너 검출 방법

• 영상 내에 정의된 윈도우 안의 픽셀 값이 상하좌우 방향으로 모두 급격하게 변하는 위치를 코너로 규정하고 이를 효과적으로 구하는 방법을 제시
• 다양한 수학적 기법(ex. 미분, 테일러 급수, 고윳값 분석)을 이용하여 입력 영상으로부터 해리스 코너 응답 함수(Harris corner response function) R을 구하고 R(x,y) 값이 충분히 큰 위치를 코너로 지정
• 엣지에서의 해리스 코너 응답 함수는 0에 가깝다.

void cornerHarris(InputArray src, OutputArray dst, int blockSize,
		          int ksize, double k, int borderType=BORDER_DEFAULT);

• src: 입력 영상, 단일채널, 8비트 또는 실수형 영상

• dst: 해리스 코너 응답 계수 값 행렬, 입력 영상과 같은 크기, CV_32FC1

  size	description
  $dst(x,y) < 0$	엣지 픽셀
  $\|dst(x,y)\|$ is small	평탄한 영역
  $dst(x,y) >> 0$	코너, local maximum 선택

• blockSize: 내부 연산에서 사용되는 이웃 픽셀 크기. 주변 blockSize x blockSize 이웃 픽셀을 이용

• ksize: (미분을 위한) 소벨 연산자 커널 크기

• k: 해리스 코너 검출 상수 (보통 0.04)

• borderType: 가장자리 픽셀 확장 방식

추적하기 좋은 특징(Good features to track)

• 1994년 Shi & Tomasi가 제안한 방법
• 해리스 코너 검출 방법을 향상시킨 코너 검출 방법
• 코너 응답 함수 정의를 다음과 같이 변경

  $R=\lambda_{1}\lambda_{2}-k(\lambda_{1}+\lambda_{2})^{2} \Longrightarrow R=min(\lambda_{1},\lambda_{2})$

• 코너 품질 함수 값이 큰 순서대로 정렬하여 코너 점을 반환
• 비최대 억제 수행

void goodFeaturesToTrack(InputArray image, OutputArray corners, 
						 int maxCorners, double qualityLevel,
                         double minDistance, InputArray mask=noArray(),
                         int blockSize=3, bool useHarrisDetector=false,
                         double k=0.04);

• image: 입력 영상, 단일채널, 8비트 또는 실수형(32비트) 영상
• corners: 검출된 코너점 좌표, vector<Point2f>
• maxCorners: 최대 코너 개수. maxCorners <= 0 이면 무제한 검출
• qualityLevel: 코너점 결정을 위한 값. 보통 0.01~0.1 사이의 값을 지정하며, 이 값이 커질수록 더욱 엄격하게 코너를 검출함
• minDistance: 코너점 사이의 최소 거리, 이보다 작은 거리에 코너들이 있을 시 하나만을 추출하도록 함
• mask: 마스크 영상, 일부 영역만을 검출 가능
• blockSize: 내부 연산에서 사용되는 이웃 픽셀 크기. 주변 blockSize x blockSize 이웃 픽셀을 이용
• useHarrisDetector: 해리스 코너 응답 함수 사용 여부
• k: 해리스 코너 응답 함수 사용 시 사용되는 파라미터

FAST 코너 검출 방법

• Features from Accelerated Segment Test
• 2006년 Rosten & Drummond가 제안한 방법
• 각각의 픽셀에 대해 픽셀을 둘러싸는 주변 16개 픽셀 값 크기를 분석하여 해당 픽셀(p) 보다 충분히 밝거나(>p+t) 또는 충분히 어두운(<p-t) 픽셀이 n개 이상 연속으로 나타나면 코너로 인식 (n은 보통 9)
• 비최대 억제 수행
• 해리스, GFTT 방법보다 매우 빠르게 동작(30배)
• https://www.edwardrosten.com/work/fast.html
• 반복 검출률이 대체로 높음
• 노이즈에 민감함

void FAST(InputArray image, std::vector<KeyPoint>& keypoints, 
          int threshold, bool nonmaxSuppresion=true);

• image: 입력 영상, 단일채널, 8비트 또는 실수형(32비트) 영상
• keypoints: 검출된 키포인트, KeyPoint 클래스의 pt 멤버(Point2f)를 이용하여 코너 좌표에 접근 가능
• threshold: 중심 픽셀 값과 주변 픽셀 값과의 차이 임계값
  (위의 설명에서 >p+t, <p-t 에서 t값)
• nonmaxSuppression: 비최대 억제 수행 여부

$\\$
$\\$

References

• 자율주행 데브코스 황선규 강사님
• 더북: Visual C++ 영상 처리 프로그래밍