PID 제어기

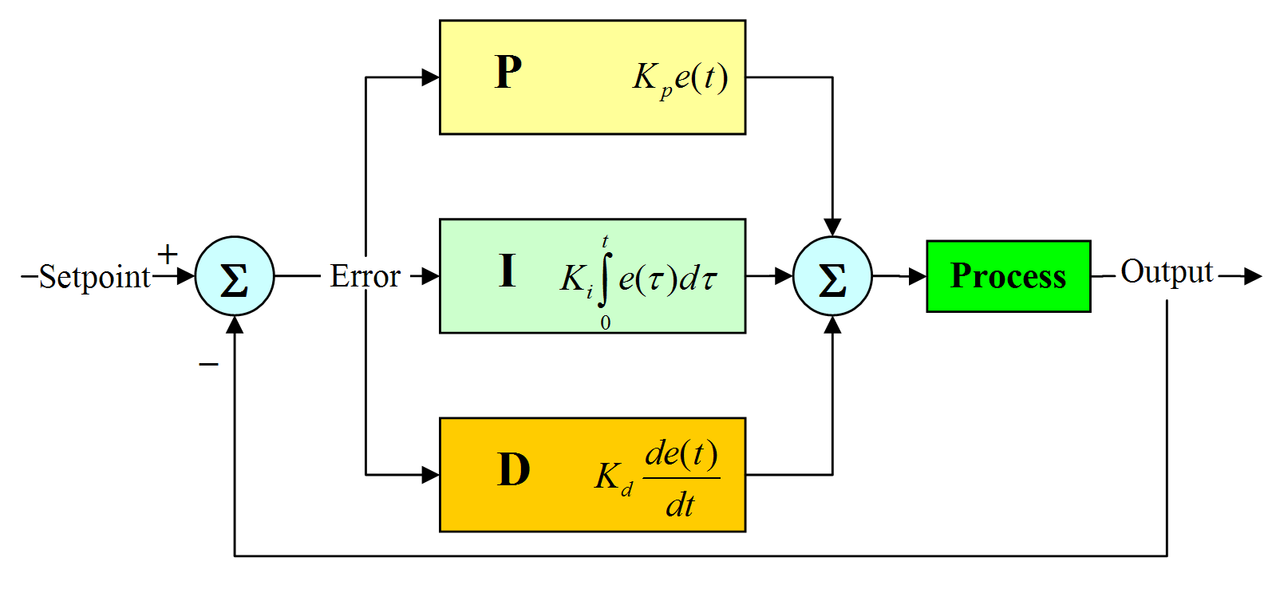
• 비례, 적분, 미분의 조합으로 적절한 값을 도출하는 기법
  • 비례: Proportional
  • 적분: Integral
  • 미분: Differential
• 제어 대상의 목표값(desired value)과 출력값(output)과의 차이로 제어값을 계산

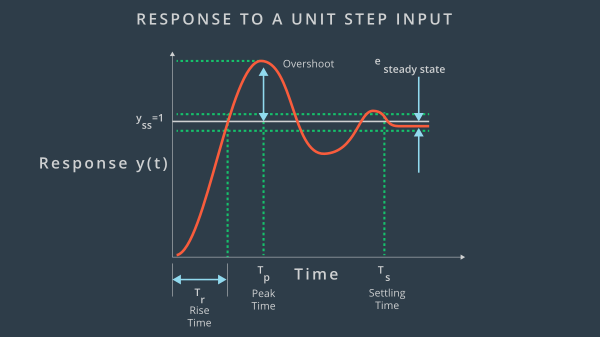
• 주요 용어와 개념

  • 오버슈트: 최종 정상상태 값을 넘어서는 상승 오차
  • 피크 시간: 가장 큰 오버슈트가 발생했을 때 시간
  • 상승 시간: output의 0.1부터 0.9까지 이를 때 걸리는 시간
  • 정착 시간: 최종 정상상태에 도달하는 시간

• PID 제어 수식

  $MV(t) = K_pe(t) +K_i\int_0^t e(\tau)d\tau+K_d\displaystyle\frac{de}{dt}$

  • $e(t)$ = Error
  • 첫번째 항: Error에 상수를 곱함
  • 두번째 항: Error를 시간에 대해 적분한 후 상수를 곱함
  • 세번째 항: Error를 시간에 대해 미분한 후 상수를 곱함

P제어 (비례: Proportional)

• 피드백 제어신호가 오차에 비례하게 만드는 비례 제어기

• 나와 목표값의 거리(오차)가 멀수록 초기에 조작량을 크게 하고, 거의 목표값에 접근해가면, 조작량은 오차에 비례하여 적어저 가는 양상을 띰

• $K_pe(t)$ = P gain x error(오차)

• $K_p$가 클 때: 오차가 작아도 출력값이 크게 변함

  • 장점: 빠른 응답속도를 가짐
  • 단점: 오버슈트(overshoot)가 발생함

• $K_p$가 작을 때: 오차가 작을수록 출력값이 작게 변함

  • 장점: 오버슈트(overshoot)가 적게 발생함
  • 단점: 느린 응답속도를 가짐

• P 제어기만 사용할 경우: 정상상태 오차가 발생함

  • 정상상태 오차(steady-state error): 반응이 일정 수준에 정착한 이후에도 존재하는 오차
  • 즉, 일정 스케일을 곱해서 출력값이 목표값에 다가갔지만, 완전히 일치하지 못하고 항상 어느 정도 마진이 남아있는 상태
  • 정상상태 오차 = (일정시간이 지난 이후 출력값) - (목표값)

• P 제어기가 없을 경우: 목표값보다 더 낮은 출력값 상태가 되어 목표값에 도달하지 못하고, 진동이 심함

P 제어 시나리오

• P gain 값을 작게 했을 때 (P-gain=1, I-gain=1, D-gain=1)

  • 반응 속도가 느림
  • 목표값에 도달은 하지만, 오버슈트가 생김

• P gain 값을 증가시켰을 때 (P-gain=5, I-gain=1, D-gain=1)

  • 반응 속도가 빨라짐
  • 빠른 반응속도 만큼 빠른 시간 내 오버슈트가 생김
  • 그러나 정상상태 오차가 발생함

I 제어 (적분: Integral)

• 적분을 이용하여 비례 제어에서 남아있는 오차를 제거하는 제어 방법

• 출력값이 목표에 빠르게 도달하고 수렴하게 함

• 정상상태 오차의 한계를 극복하기 위해, P제어를 통해 목표값에 어느 정도 도달했을 때 그 시점부터 작은 오차들을 누적하여 목표값에 근접할 수 있도록 도와줌

• $K_i\displaystyle\int_0^te(\tau)d\tau$ = I gain x 누적 Error

• $K_i$가 클 때: 누적 오차가 빠르게 증가함

  • 장점: 빠른 응답 속도를 가짐
  • 단점: 오버 슈트(overshoot)가 크게 발생함

• $K_i$가 작을 때: 누적 오차가 느리게 증가함

  • 장점: 오버 슈트가 작게 발생함
  • 단점: 느린 응답 속도를 가짐

• I 제어기를 사용할 경우:

  • 정상상태 오차를 줄일 수 있음
  • 오차가 없는 상태에도 I 제어기에 남아있는 누적 오차 때문에 제어값이 계속 발생함
  • P 제어만으로 부족하므로 보통 PI, PID 제어기를 많이 사용함

I 제어 시나리오

• I gain값을 증가시켰을 때 (P-gain=5, I-gain=2, D-gain=1)
  • 반응 속도가 빨라지고, 정상상태 오차가 없어짐
  • 그러나, 오버슈트가 크게 발생함

D 제어 (미분: Differential)

• 미분을 이용하여 진동을 줄이고 안정성을 향상시키는 제어 방법

• 급격한 출력값의 변동이 발생할 때 급격하게 변하지 않도록 함

  • 즉 반대방향으로 브레이크를 거는 역할

• 오차가 상수일 경우 D제어기의 출력은 0이 되어 정상상태 오차를 줄일 수 없음

  • 일반적으로 단독으로 D제어기만 사용하지는 않음

• 특정 신호가 급변하는 경우 미분 제어기의 출력이 급격하게 커져 시스템을 파괴하는 경우도 있음

  • 예를 들어, 출력값이 완만하다가 갑자기 훅 솟으면, 이때의 미분값이 매우 커지면서 시스템이 다운될 수 있음

• $K_d\displaystyle\frac{de}{dt}$ = D gain x Error 변화량

  • Error 변화량은 출력값과 목표값에 대한 Error를 표현한 그래프에 대한 미분값을 의미하며, 이 그래프는 보통 우하향 하는 양상을 띰
  • 기울기가 가파를수록 더 많이 브레이크를 거는 행위를 한다고 생각할 수 있음
  • 예를들어 P 제어기 수치를 크게 하면, 반응속도를 빠르게 하여 출력값과 목표값이 가까워 지게 되며 그에 상응하는 미분값이 커지게 되므로 반대 방향으로 더 많은 브레이크를 걸게 됨

• $K_d$가 클 때

  • 장점: 오버슈트가 작게 발생함
  • 단점: 신호가 급변하는 경우 시스템을 파괴할 수 있음

• $K_d$가 작을 때

  • 장점: 신호가 급변하더라도 적절한 피드백을 할 수 있음
  • 단점: 오버슈트가 크게 발생함

• D 제어기를 사용할 경우:

  • 시스템의 안정도를 증가시킬 수 있음
  • 미분이 불가능한 오차인 경우, 적절한 제어가 되지 않을 수 있음

D 제어 시나리오

• D gain값을 증가시켰을 때 (P-gain=5, I-gain=2, D-gain=2.5)
  • 오버슈트가 발생함

PID 제어기가 없는 경우

• 원하는 결과값에 도달하지 못함
• 진동이 심함

PID 제어 시나리오

• P gain=1, I gain=1, D gain=1:

  • 목표하는 값에 도달하지만, 오버슈트가 발생하고, 반응속도가 느림

• P gain=5, I gain=1, D gain=1:

  • 오버슈트가 여전히 발생하지만, 빠른 응답속도를 가짐
  • 정상상태 오차가 발생함

• P gain=5, I gain=2, D gain=1:

  • 오버슈트는 커졌지만 정상상태 오차가 없어짐
  • 빠른 반응속도를 가짐

• P gain=5, I gain=2, D gain=2.5:

  • 작은 오버슈트를 가지고, 정상상태 오차가 없음

이상적인 제어 결과

• 빠른 응답속도를 가짐

• 오버슈트가 발생하지 않음

• 정상상태 오차가 발생하지 않음

• gain 값 사이의 trade-off 때문에 한쪽이 좋아지면 다른 한쪽이 나빠지게 되므로 현실적으로 가능하지 않음

  • 따라서 적절히 타협을 보아야 함
  • 타협의 기준을 ( )% 이하의 오버슈트, ( )sec 의 정착시간 등으로 설정함
  • 주로 5% 이내의 오버슈트, 0.2초 이내의 정착시간을 설정함

allpass, lowpass, highpass filter 연관성

PID 제어기를 주파수 영역에서 해석해 보면, 각 항이 특정한 필터 특성과
유사하다는 것을 알 수 있습니다.

P(비례) 항

• 주파수 응답 상에서 일정한 이득(Gain, $𝐾_p$)으로 작동합니다.
• 특정 주파수를 강조하거나 감쇠하지 않고, 전 대역에 걸쳐 동일한 비율로 증폭하기 때문에, 흔히 All-pass 필터(출력 위상을 제외하면 전 주파수대의 진폭 특성이 동일)와 비슷한 역할을 합니다.

I(적분) 항

• 적분 연산은 라플라스 영역에서 $1/s'$, 즉 주파수 영역에서 $1/jw$에 해당합니다.
• ω가 높아질수록(고주파) 이득이 작아집니다.
• ω가 낮을수록(저주파) 이득이 커지므로, Low-pass 필터로 볼 수 있습니다.
• 실제로 적분 항이 저주파 대역(장기 누적 오차)에 세게 반응하며, 고주파 잡음에는 둔감합니다.

D(미분) 항

• 미분 연산은 라플라스 영역에서 $s$, 주파수 영역에서 $1/jw$ 형태입니다.
• ω가 높아질수록(고주파) 이득이 커지므로, High-pass 필터에 해당합니다.
• 작은 순간 변화(급격한 오차 변화)에 민감하게 반응하므로, 잡음이 많은 실환경에서는 노이즈 증폭 문제가 발생할 수 있습니다.
  

References

• controls in robotics
• 자이트론 김선영 강사님