영상의 기하학적 변환

• 영상을 구성하는 픽셀의 배치 구조를 변경함으로써 전체 영상의 모양을 바꾸는 작업
• 상하좌우 대칭 처리 등 전처리 작업, 두 영상의 같은 객체를 찾는 영상 정합(image registration), 왜곡 제거 등

$\\$
$\\$

기하학적 변환의 종류

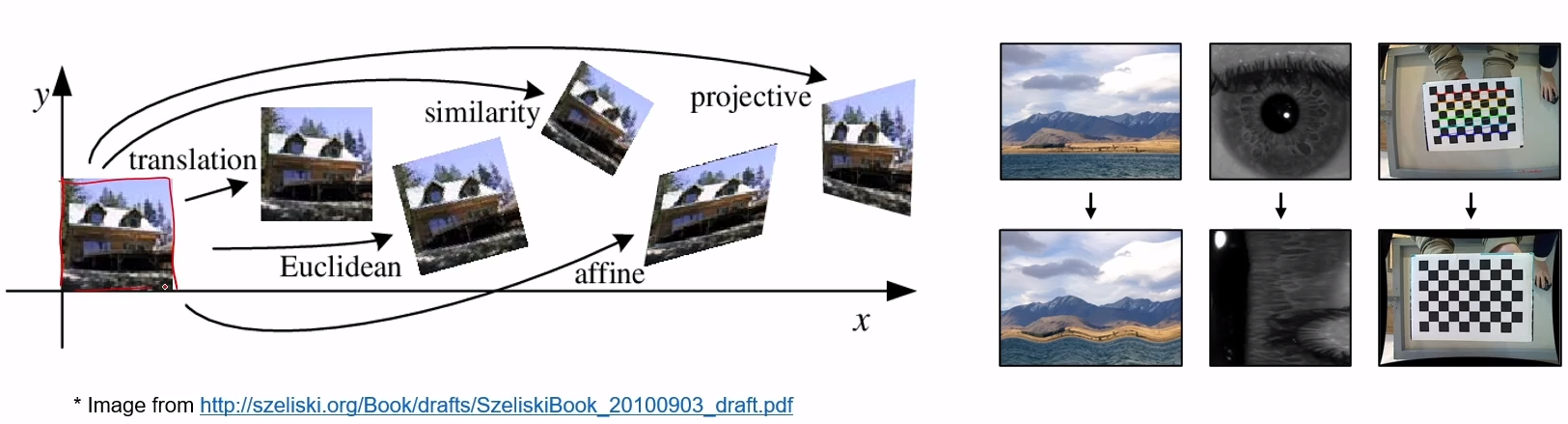
• translation
• sheer
• scale
• euclidean, rigid
• similarity
• affine
• projective

$\\$
$\\$

이동 변환 (translation transform)

• 가로 또는 세로 방향으로 영상을 특정 크기만큼 이동시키는 변환
• x축과 y축 방향으로의 이동 변위를 지정
• 2 x 3 행렬: affine transform matrix 라고 함

  $\begin{bmatrix}x^{\prime} \\y^{\prime} \end{bmatrix}= \begin{bmatrix}1 & 0 & a \\0 & 1 & b \end{bmatrix} \begin{bmatrix}x \\y \\1 \end{bmatrix}$

$\\$
$\\$

전단 변환 (sheer transform)

• 직사각형 형태의 영상을 한쪽 방향으로 밀어서 평행사변형 모양으로 변형되는 변환. 층밀림 변환
• 가로 방향 또는 세로 방향으로 따로 정의됨

  $\begin{bmatrix}x^{\prime} \\y^{\prime} \end{bmatrix}= \begin{bmatrix}1 & m \\0 & 1 \end{bmatrix} \begin{bmatrix}x \\y \end{bmatrix}$

  $\begin{bmatrix}x^{\prime} \\y^{\prime} \end{bmatrix}= \begin{bmatrix}1 & 0 \\m & 1 \end{bmatrix} \begin{bmatrix}x \\y \end{bmatrix}$

$\\$
$\\$

크기 변환 (scale transform)

• 영상의 크기를 원본 영상보다 크게 또는 작게 만드는 변환
• x축과 축 방향으로 스케일 비율(scale factor)를 지정
• 2 x 3 행렬: affine transform matrix 라고 함

  $\begin{bmatrix}x^{\prime} \\y^{\prime} \end{bmatrix}= \begin{bmatrix}s_x & 0 & 0\\0 & s_y & 0\end{bmatrix} \begin{bmatrix}x \\y \\1 \end{bmatrix}$

• [ISSUE] 순방향 매핑 (forward mapping): 영상 확대 시 빈 공간이 발생

  for (int y=0; y<src.rows; y++) {
  	for (int x=0; x<src.cols; x++) {
      	int x_ = x * 2;
          iny y_ = y * 2;
          dst.at<uchar>(y_, x_) = src.at<uchar>(y, x);
      }
  }

• 역방향 매핑 (backward mapping)

  $\begin{cases}x^\prime = s_x x\\y^\prime = s_y y\end{cases} \Longrightarrow \begin{cases}x = x^\prime/s_x\\ y= y^\prime/s_y\end{cases}$

  for (int y_=0; y_<dst.rows; y_++) {
  	for (int x_=0; x_<dst.cols; x_++) {
      	int x = x_ / 2;
          int y = y_ / 2;
          dst.at<uchar>(y_, x_) = src.at<uchar>(y,x);
      }
  }

$\\$
$\\$

보간법 (Interpolation)

• 보간법이란 실수 좌표 상에서의 픽셀 값을 결정하기 위해 주변 픽셀 값을 이용하여 값을 추정하는 방법
• 역방향 매핑에 의한 크기 변환 시, 참조해야 할 입력 영상의 (x,y) 좌표가 실수 좌표라면?
  • (x,y)와 가장 가까운 정수 좌표의 픽셀 값을 참조하거나,
  • 또는 (x,y) 근방의 정수 좌표 픽셀 값을 이용하여 실수 좌표 위치의 픽셀 값을 추정

보간법 종류

• 최근방 이웃 보간법 (nearest neighbor interpolation)
  • 가장 가까운 위치에 있는 픽셀의 값을 참조하는 방법
  • ex: (50.2, 32.8) -> (50, 33)
  • 빠르고 구현이 쉽지만 계단 현상, 블록 현상이 나타남
• 양선형 보간법 (bilinear interpolation)
  • 실수 좌표를 둘러싸고 있는 네 개의 픽셀 값에 가중치를 곱한 값들의 선형 합으로 결과 영상의 픽셀 값을 구하는 방법
  • 최근방 이웃 보간법에 비해서는 느린 편이지만, 비교적 빠르며 계단 현상이 크게 감소
• 3차 보간법 (cubic interpolation)
  • 실수 좌표를 둘러싸고 있는 16개의 픽셀 값에 3차 함수를 이용한 가중치를 부여하여 결과 영상 픽셀의 값을 계산
• 스플라인 보간법 (spline interpolation)
• 란쵸스 보간법 (lanczos interpolation)

보간법 관련 resize 함수

void resize(InputArray src, OutputArray dst, Size dsize,
			double fx=0, double fy=0, int interpolation=INTER_LINEAR);

• src, dst : 입력 영상, 출력 영상

• dsize : 결과 영상의 크기, Size()를 지정하면 fx, fy에 의해 자동 결정됨

• fx, fy : x, y 방향 스케일 비율 (dsize=0일 때 유효)

• interpolation : 보간법 지정 상수

  type	description
  INTER_NEAREST	최근방 이웃 보간법
  INTER_LINEAR	양선형 보간법 (2x2 이웃 픽셀 참조)
  INTER_CUBIC	3차회선 보간법 (4x4 이웃 픽셀 참조)
  INTER_LANCZOS4	Lanczos 보간법 (8x8 이웃 픽셀 참조)
  INTER_AREA	영상 축소 시 효과적

• 영상 축소 시 유의사항:
  • 한 픽셀로 구성된 선분들은 영상을 축소할 때 사라지는 경우가 발생
  • 입력 영상을 부드럽게 필터링한 후 축소하거나 다단계 축소 권장
  • OpenCV의 resize() 함수에서는 INTER_AREA 플래그를 사용

$\\$
$\\$

회전 변환 (rotation transform)

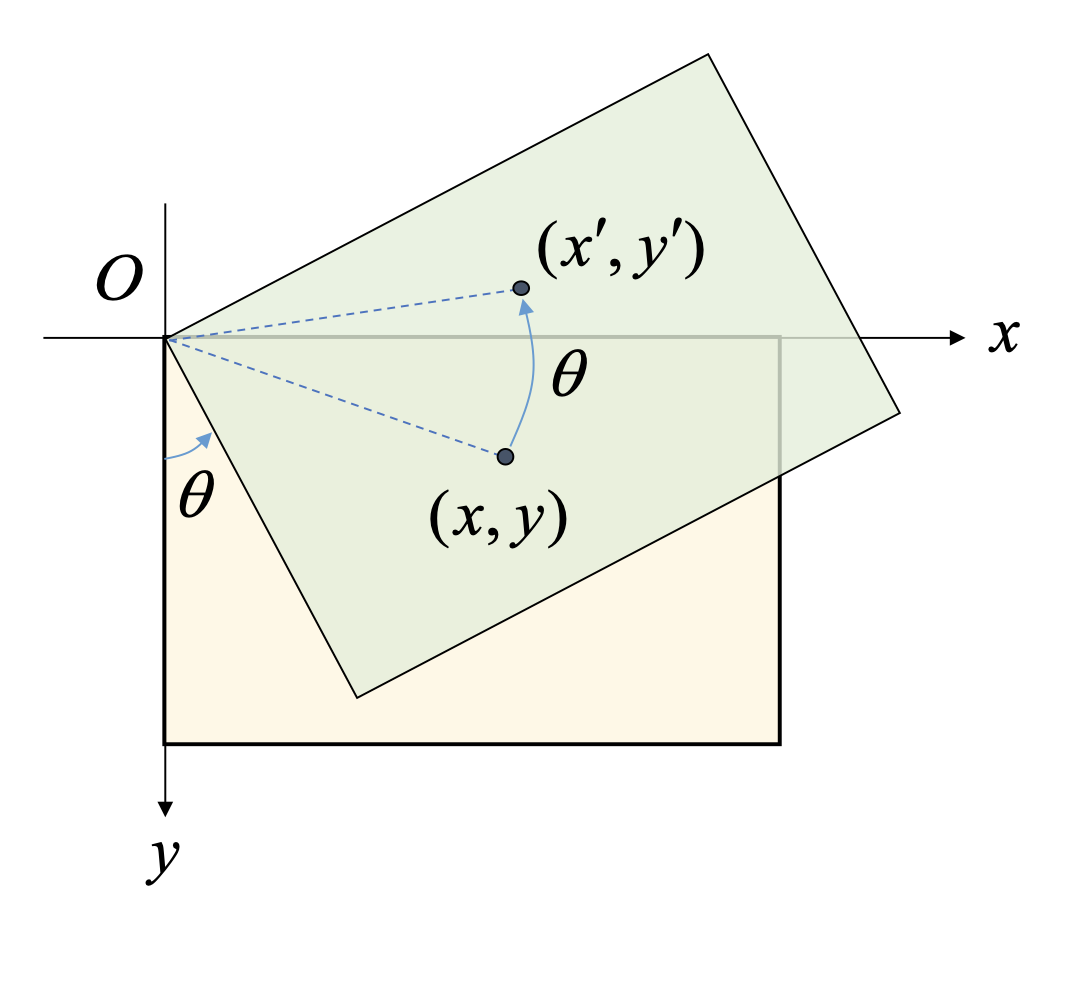
• 영상을 특정 각도만큼 회전시키는 변환
• OpenCV는 반시계 방향을 기본으로 사용

  $\begin{bmatrix}x^{\prime} \\y^{\prime} \end{bmatrix}= \begin{bmatrix}cos\theta & sin\theta & 0 \\-sin\theta & cos\theta & 0 \end{bmatrix} \begin{bmatrix}x \\y \\1 \end{bmatrix}$

• 회전 변환과 역방향 매핑
  • 회전 변환도 역방향 매핑으로 구현해야 빈 픽셀이 발생하지 않음

    $\begin{bmatrix}x^{\prime} \\y^{\prime} \end{bmatrix}= \begin{bmatrix}cos\theta & sin\theta \\-sin\theta & cos\theta \end{bmatrix} \begin{bmatrix}x \\y \end{bmatrix} \Longrightarrow \begin{bmatrix}x \\y\end{bmatrix}= \begin{bmatrix}cos\theta & -sin\theta \\sin\theta & cos\theta \end{bmatrix} \begin{bmatrix}x^{\prime} \\y^{\prime} \end{bmatrix}$

  • 보간법 선택 가능

getRotationMatrix2D()

• 원리: 이미지 중심으로 이동 변환 후 로테이션(회전 변환)을 진행 후, 다시 이미지를 이동 변환시켜 원래 제자리에 가져다 놓음

Mat getRotationMatrix2D(Point2f center, double angle, double scale);

• center : 회전 중심 좌표, 보통은 이미지 중심을 많이 사용하며, Point2f pt(src.cols/2.f, src.rows/2.f);
• angle : 반시계방향 회전 각도(degree), 음수는 시계방향
• scale : 회전 후 확대 비율
• 반환값 : 2x3 double(CV_64F) 행렬, affine transformation matrix

  $\begin{bmatrix}\alpha & \beta & (1-\alpha)*center.x-\beta*center.y \\ \beta & \alpha & \beta*center.x+(1-\alpha)*center.y\end{bmatrix}$ where $\begin{cases}\alpha=scale*cos(angle)\\\beta=scale*sin(angle)\end{cases}$

어파인 변환

Mat warpAffine(InputArray src, OutputArray dst, Size dsize,
			   int flags=INTER_LINEAR, int borderMode=BORDER_CONSTANT,
               const Scalar& borderValue=Scalar());

• src : 입력 영상
• dst : 출력 영상, src와 같은 타입
• M : 2x3 어파인 변환 행렬, CV_32F 또는 CV_64F
• dsize : 결과 영상의 크기 (Size()로 채우면 src의 크기와 같음)
• flags : 보간법 선택
• borderMode : 가장자리 픽셀 처리 방식
• borderValue : BORDER_CONSTANT 모드 사용 시 비어있는 공간 채울 픽셀 값

$\\$
$\\$

동차 좌표계 (homogeneous coordinates)

• 차원의 좌표를 1차원 증가시켜 표현하는 방법
• 예를 들어, 2차원 (x,y) 좌표를 (x,y,1)로 표현
• 동차 좌표계를 사용한 이동 변환 -> 크기 변환 -> 회전 변환

  $\begin{bmatrix}x^{\prime} \\y^{\prime} \\ 1 \end{bmatrix}= \begin{bmatrix}cos\theta & sin\theta & 0 \\-sin\theta & cos\theta & 0 \\0 & 0 & 1\end{bmatrix} \begin{bmatrix}s_x & 0 & 0\\0 & s_y & 0 \\0 & 0 & 1\end{bmatrix} \begin{bmatrix}1 & 0 & a \\0 & 1 & b \\0 & 0 & 1\end{bmatrix} \begin{bmatrix}x \\y \\1 \end{bmatrix}$

$\\$
$\\$

영상의 대칭 변환

• 원리: 크기 변환 & 이동 변환의 조합
• 상하 대칭
• 좌우 대칭
• 좌우 상하 대칭

Mat flip(InputArray src, OutputArray dst, int flipCode);

• src : 입력 영상

• dst : 출력 영상

• flipCode : 대칭 방향 지정

  type	description
  양수 (+1)	좌우 대칭
  0	상하 대칭
  음수 (-1)	좌우 & 상하 대칭

$\\$
$\\$

References

• 자율주행 데브코스 황선규 강사님