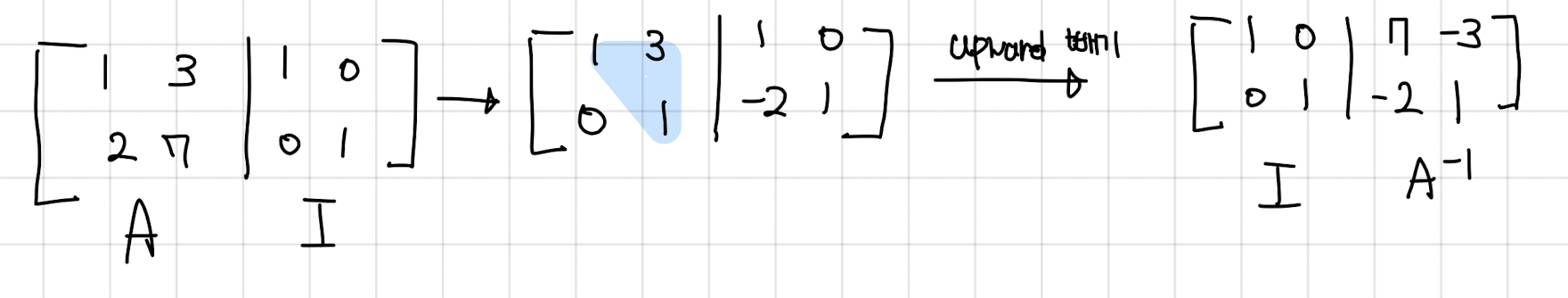
Lecture 3

keyword: Matrices Multiplication, Inverse Matrices

1. Matrix Multiplication (행렬 곱을 수행하는 다양한 방법)

• 행렬 곱의 조건: Matrix A Matrix B 를 가능하게 하려면, A가 (m×n) 크기일 때 B가 (n×p) 크기여야 함.
  → AB = C에서 C의 크기는 (m×p)

1. Row vector와 column vector의 내적 (Inner product)값의 조합

   

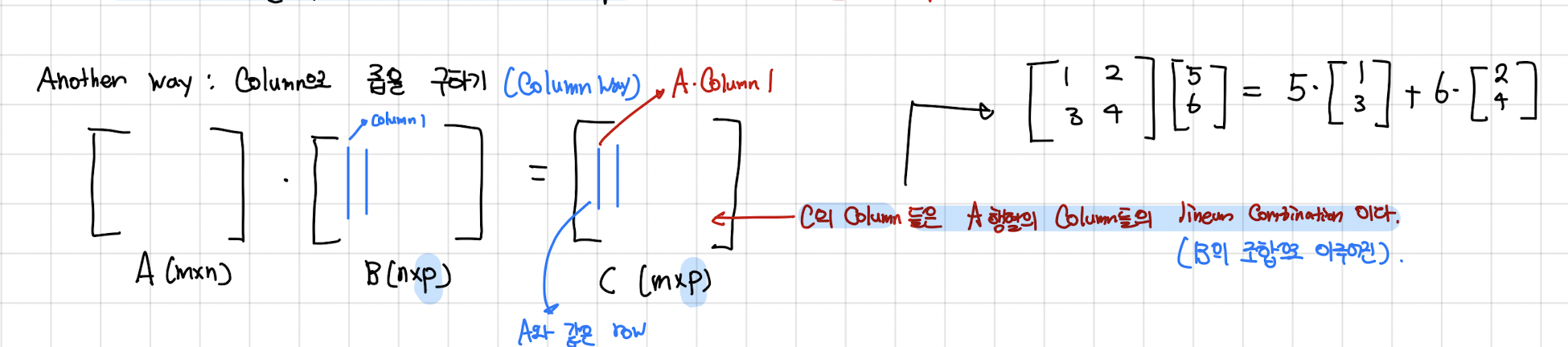
2. A Matrix의 Column들의 Linear Combination으로 행렬 곱을 표현

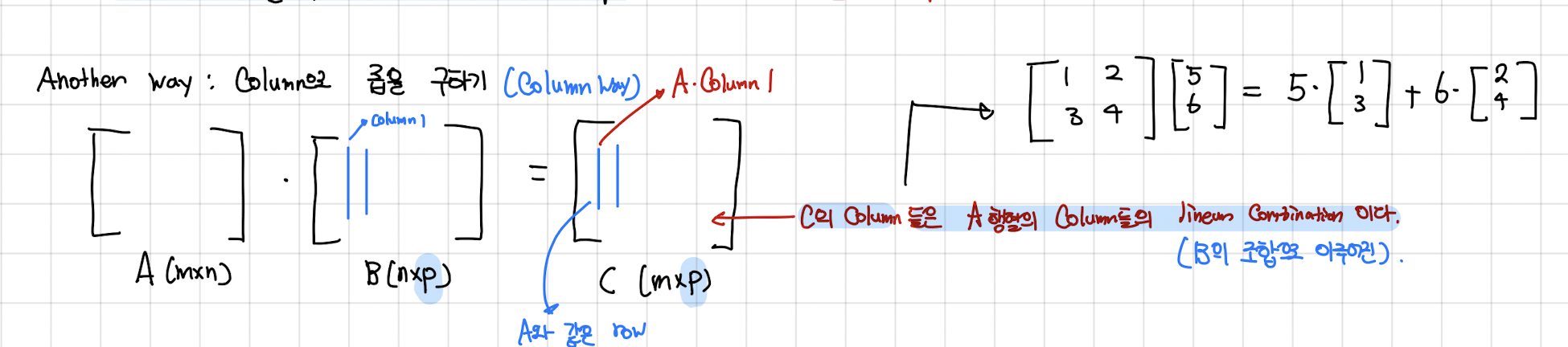
• C의 Column들은 A행렬 Column들을 B행렬 Column의 Weight으로 Linear Combination한 Vector이다.

1. B Matrix의 Row들의 Linear Combination으로 행렬 곱을 표현

• C의 Row들은 B행렬 Row들을 A행렬 Row의 Weight로 Linear Combination한 Vector이다.

1. Matrix dot product decomposition

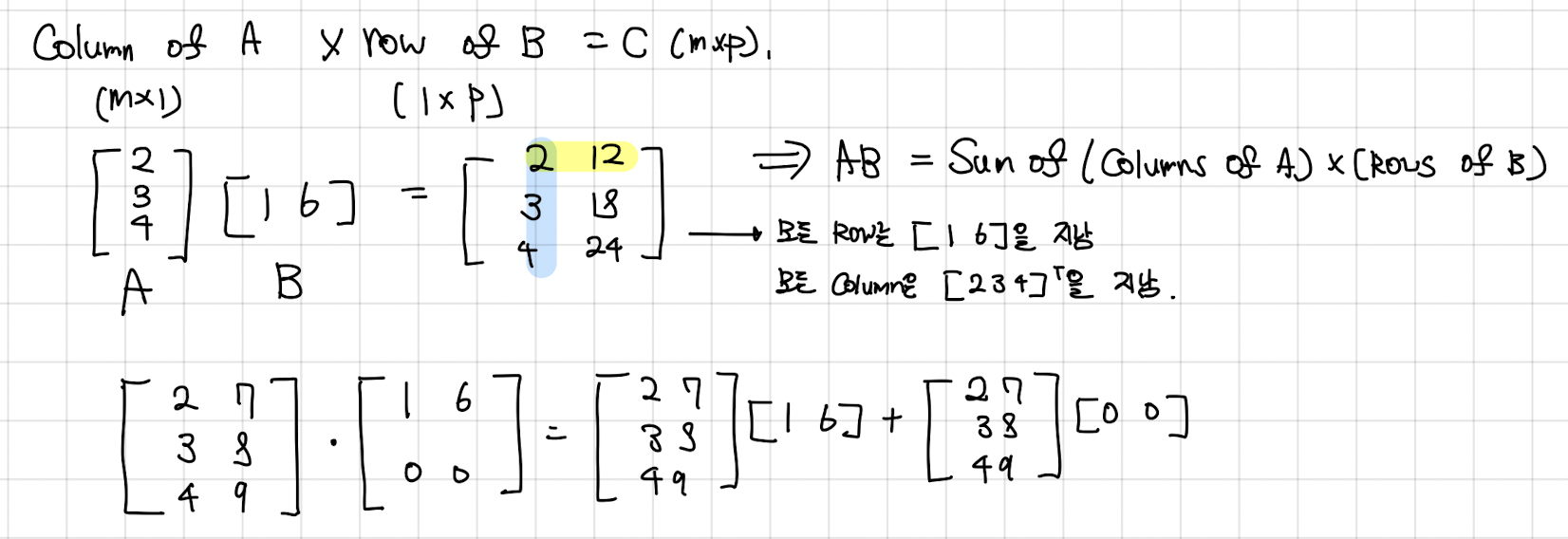
• 행렬 곱 A×B를 A×B’row1 + A×B’row2로 분해

2. Inverse Matrix (역행렬)

1. Inverse condition

   

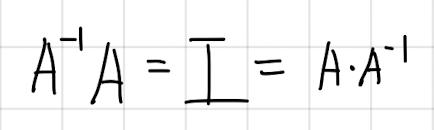
• 위의 식이 성립하는 경우 역행렬이 존재한다, 즉 행렬 A가 invertible 혹은 non-singular 한다고 한다.

  

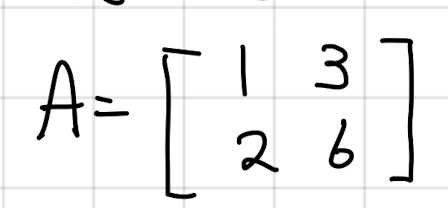
위의 예시에서 역행렬이 존재하지 않는 이유 (Matrix A가 Singular 혹은 non-invertible한 경우)

1. 행렬의 고유값(Determinant)이 0이다.
2. 2 Column이 같은 선상에 존재하기 때문에, 두 Column간의 선형 조합이 그 선에서 머무른다.
3. Ax=0을 만들 수 있는 Vector X (non-zero) 가 존재하면, A는 역행렬이 없다.

• X ≠ 0 이므로 A^(-1) 이 존재할 수 없다.

1. How to get inverse?

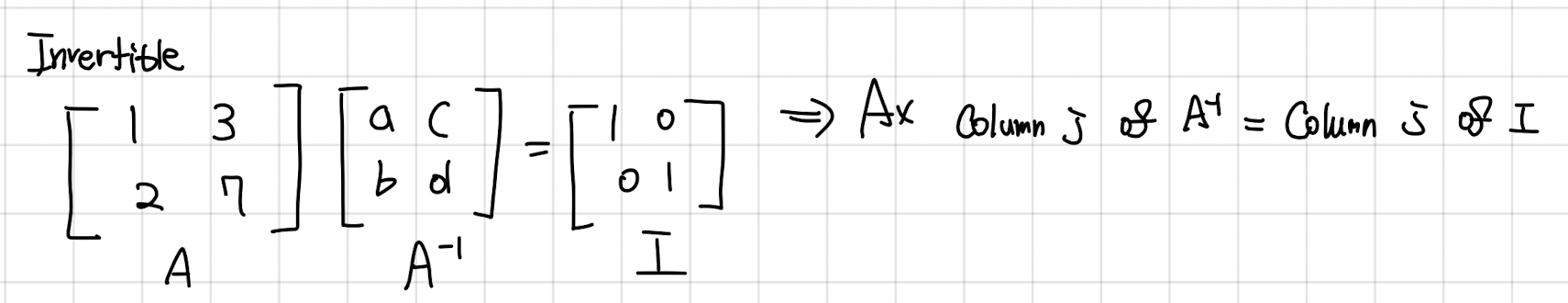
• Gauss-Jorden (Solve to equations at once)

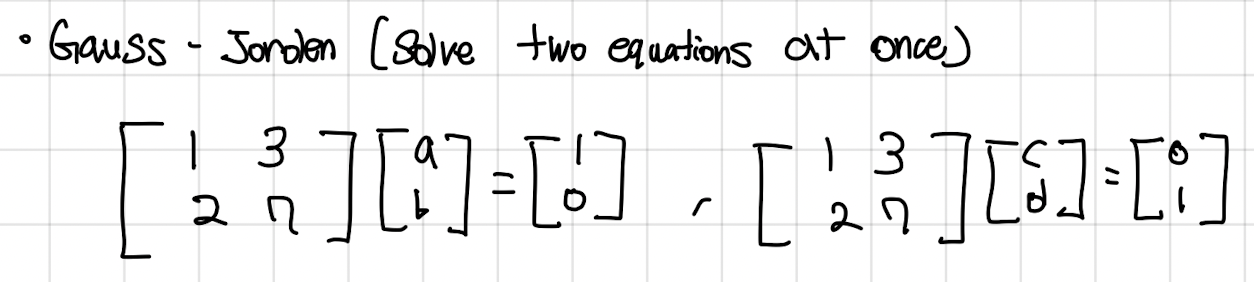
• 위와 같은 식으로 [a;b], [c;d]를 따로 구하는 것이 아닌 한번에 구함. (변환 행렬 E)