KMP(Knuth-Morris-Pratt)

• Rabin Karp 알고리즘을 이용하면 길이가 각각 n, m인 두 문자열 T(=text), P(=pattern)가 주어졌을 때 문자열 T의 부분 문자열 중 문자열 P와 일치하는 경우가 있는지를 O(N+M)에 구할 수 있다고 했습니다. 이렇게 부분 문자열로서 어디에서 일치하는지를 O(N+M)에 찾아낼 수 있는 또 다른 알고리즘이 있습니다. 바로 KMP Algorithm 입니다.
• 불일치가 발생한 텍스트 문자열의 앞 부분에 어떤 문자가 있는지를 미리 알고 있으므로, 불일치가 발생한 앞 부분에 대하여 다시 비교하지 않고 매칭을 수행
• 패턴을 전 처리하여 부분 일치 테이블 배열 fail[k]을 구해서 잘못된 시작을 최소화함

Failure Function

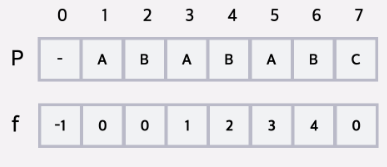
• fail[k] : 문자열 P에서 [1, i]로 이루어진 문자열 중 접두사와 접미사가 일치하는 최장 길이를 뜻 단, 자기 자신은 제외
  

백준 1786. 찾기

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.List;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        String s = br.readLine();
        String s1 = br.readLine();
        char[] text = s.toCharArray();
        char[] pattern = s1.toCharArray();
        int[] fail = makeTable(pattern);
        System.out.println(kmp(fail, text, pattern));
    }

    private static String kmp(int[] fail, char[] text, char[] pattern) {
        StringBuilder sb = new StringBuilder();
        List<Integer> result = new ArrayList<>();
        int j = 0;
        for (int i = 0; i < text.length; i++) {
            while (j > 0 && text[i] != pattern[j])
                j = fail[j-1];
            if(text[i] == pattern[j]){
                if(j == pattern.length-1){
                    result.add(i-j+1);
                    j = fail[j];
                }else{
                    ++j;
                }
            }
        }
        sb.append(result.size()).append("\n");
        for (Integer i : result) {
            sb.append(i).append(" ");
        }
        return sb.toString();
    }

    private static int[] makeTable(char[] pattern) {
        int[] fail = new int[pattern.length];
        int j = 0;
        for (int i = 1; i < pattern.length; i++) {
            while (j > 0 && pattern[j] != pattern[i])
                j = fail[j-1];
            if(pattern[j] == pattern[i]) fail[i] = ++j;
        }
        return fail;
    }
}