모든 쌍 최단 경로

최단 경로

• 한 도시에서 다른 도시로 가장 빨리 갈 수 있는 경로를 찾는 문제
• 가중치 포함, 방향성 그래프에서 최단경로 찾기
• 최적화 문제(optimization problem)
  • 주어진 문제에 대하여 하나 이상의 많은 해답이 존재할 때, 이 가운데에서 가장 최적인 해답(optimal solution)을 찾아야 하는 문제

brute-force 접근 방법

• 한 정점에서 다른 정점으로의 모든 경로를 구한 뒤, 그들 중에서 최단 경로를 찾는다.
• 그래프가 n개의 정점을 가지고 있고, 완전그래프라고 가정하면
• 한 정점 i에서 어떤 정점 j로 가는 경로들을 다 모아 보면, 그 졍로들 중에서 나머지 모든 정점을 한번씩은 꼭 거쳐서 가는 경로들도 포함되어 있는데, 그 경로들의 수만 우선 계산해 보자
• i에서 출발하여 처음에 도착할 수 있는 정점의 가지 수는 n-2개 이고, 그 중에 하나를 선택하면, 그 다음에 도착할 수 있는 정점의 가지수는 n-3개 이고, 이렇게 계속해서 계산해 보면, 총 경로의 개수는 (n-2)(n-3)…1 = (n-2)! 이 된다
• 이 경로의 개수만 보아도 지수보다 훨씬 크므로, 이 알고리즘은 절대적으로 비효율적이다

DP 접근 방법

• 이 문제를 해결하려면, 각 정점을 시작 정점으로 정하여 다익스트라(Dijkstra)의 최단 경로 알고리즘을 수행하면 된다
• 이때의 시간 복잡도는 인접행렬을 사용하면 O(n^3) 이다. 단, n은 정점의 수이다
• Warshall은 그래프에서 모든 쌍의 경로 존재 여부 (transitive closure)를 찾아내는 동적 계획 알고리즘을 제안했고, Floyd는 이를 변형하여 모든 쌍 최단 경로를 찾는 알고리즘을 고안하였다
• 따라서 모든 쌍 최단 경로를 찾는 동적 계획 알고리즘을 플로이드 워샬 알고리즘이라고 한다
• 플로이드 알고리즘의 시간 복잡도는 O(n^3) 으로 다익스트라의 시간복잡도와 동일하다
• 그러나 플로이드 알고리즘은 매우 간단하여 다익스트라 알고리즘을 사용하는 것보다 효율적이다
• 동적 계획 알고리즘으로 모든 쌍 최단 경로 문제를 해결하려면 먼저 부분문제들을 찾아야 한다
• 이를 위해 일단 그래프의 정점의 수가 적을 때를 생각해보자
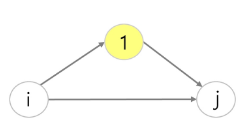
• 그래프에 3개의 정점이 있는 경우, 정점 i에서 정점 j까지의 최단 경로를 찾으려면 2가지 경로, 즉, 정점 i에서 정점 j로 직접가는 경로와 정점 1을 경유하는 경로 중에서 짧은 것을 선택하면 된다
  
• 정점 1로부터 시작하여, 정점 1과 2, 그 다음엔 정점 1, 2, 3으로 하나씩 추가하여, 마지막에는 정점 1~n 까지의 모든 정점을 경유 가능한 정점들로 고려하면서, 모든 쌍의 최단 경로의 거리를 계산한다
• 부분 문제 정의: 단, 입력 그래프의 정점을 각 1, 2, 3, …, n이라 하자
  • $D_{ij}^k$ = 정점 {1, 2, 3, …, k} 만을 경유 가능한 정점들로 고려하여, 정점 i로 부터 정점 j까지의 모든 경로 중에서 가장 짧은 경로의 거리
• 여기서 주의할 것은 정점 1에서 정점 k까지의 모든 정점들을 반드시 경유하는 경로를 의미하는 것이 아니다
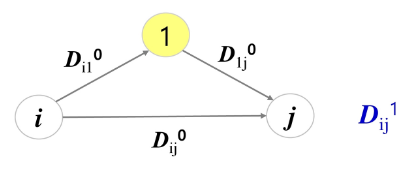
• 여기서 k ≠ i, k ≠ j 이고, k = 0인 경우, 정점 0은 그래프에 없으므로 어떤 정점도 경유하지 않는다는 것을 의미한다. 따라서 $D_{ij}^0$은 입력으로 주어지는 간선 (i, j)의 가중치이다
• $D_{ij}^1$은 i에서 정점 1을 경유하여 j로 가는 경로와 i에서 j로 직접가는 경로중에서 짧은 거리이다
• 따라서 모든 쌍 i와 j에 대하여 $D_{ij}^1$을 계산하는 것이 가장 작은 부분 문제들이다. 단, i ≠ 1, j ≠ 1이다
  

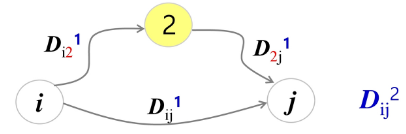
• 그 다음엔 i에서 정점 2를 경유하여 j로 가는 경로의 거리와 $D_{ij}^1$ 중에서 짧은 거리를 $D_{ij}^2$로 정한다
• 단, 정점 2를 경유하는 경로의 거리는 $D_{i2}^1$ + $D_{2j}^1$ 이다
• 모든 쌍 i와 j에 대하여 $D_{ij}^2$를 계산하는 것이 그 다음으로 큰 부분 문제들이다. 단 i ≠ 2, j ≠ 2이다
  

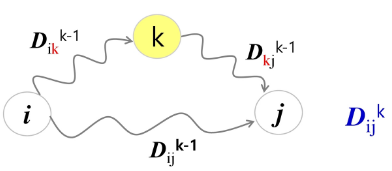
• k를 계속 늘려 정점 i에서 정점 k를 경유하여 j로 가는 경로의 거리와 $D_{ij}^{k-1}$중에서 짧은 거리를 $D_{ij}^k$로 정한다
• 단, 정점 k를 경유하는 경로의 거리는 $D_{ik}^{k-1}$ + $D_{kj}^{k-1}$이고, i ≠ k, j ≠ k이다
  

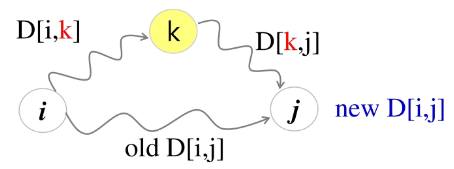
• 이런 방식으로 k가 1에서 n이 될 때까지 $D_{ij}^k$를 계산해서, $D_{ik}^n$, 즉, 모든 정점을 경유 가능한 정점들로 고려한 모든 쌍 i와 j의 최단 경로의 거리를 찾는 방식이 플로이드의 모든 쌍 최단 경로 알고리즘이다
  

• 모든 쌍 최단 경로 알고리즘

D[i][j] = 정점 i에서 정점 j로의 최소 비용
AllPairsShortest(D[][])
	FOR k in 1 -> n
		FOR i in 1 -> n      (단, i != k)
			FOR j in 1 -> n    (단, j != k, j != i)
				D[i][j] <- min(D[i][k] + D[k][j], D[i][j])

• Line 1의 for 루프는 k가 1에서 n까지 변하는데, 이는 경유 가능한 정점을 1부터 n까지 확장 하는것
• Line 2~3 : 점들의 각 쌍을 하나씩 고려하기 위한 루프 (단, i = j 또는 i = k 또는 j = k의 경우 제외)
• Line 4 : 각 정점의 쌍 i, j에 대해 i에서 j까지의 거리가 k를 포함하여 경유하는 경로의 거리, 즉, D[i][k] + D[k][j] 와 정점 {1, 2, …, (k-1)}만을 경유 가능한 점들로 고려하여 계산된 최단 경로의 거리가 D[i][j] 가 짧은지를 결정하여 D[i][j] 를 갱신한다

시간 복잡도

• 플로이드 워샬 알고리즘의 시간복잡도는 위의 예제에서 보았들이 각 k에 대해서 모든 i, j 쌍에 대해 계산되므로, 총 n * n * n = n^3 회 계산이 이루어지고, 각 계산은 O(1) 시간이 걸린다
• 따라서 시간 복잡도는 $O(n^3)$이다

백준 11404 플로이드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;

/**
 *  시간 : 304ms, 메모리 : 41,756KB
 */
public class 백준_11404_플로이드 {
    static int[][] dist;
    static int n, m, from, to, weight;
    static final int INF = 100_000_000;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st;
        StringBuilder sb = new StringBuilder();
        n = Integer.parseInt(br.readLine());
        m = Integer.parseInt(br.readLine());
        dist = new int[n][n];
        for (int i = 0; i < n; i++) {
            Arrays.fill(dist[i], INF);
            dist[i][i] = 0;
        }
        for (int i = 0; i < m; i++) {
            st = new StringTokenizer(br.readLine());
            from = Integer.parseInt(st.nextToken());
            to = Integer.parseInt(st.nextToken());
            weight = Integer.parseInt(st.nextToken());
            dist[from-1][to-1] = Math.min(dist[from-1][to-1], weight);
        }
        for (int k = 0; k < n; k++) {
            for (int i = 0; i < n; i++) {
                for (int j = 0; j < n; j++) {
                    dist[i][j] = Math.min(dist[i][j], dist[i][k] + dist[k][j]);
                }
            }
        }
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                sb.append(dist[i][j] == INF ? 0 : dist[i][j]).append(" ");
            }
            sb.append("\n");
        }
        System.out.print(sb);
        br.close();
    }
}